Глава 7. Неопределенный интеграл
§7.1. Определение и свойства неопределенного интеграла
Предположим, что на некотором промежутке
определена непрерывная функция
.
Первообразной функции
на промежутке
называется функция
такая, что
при любом
.
Теорема (об общем виде всех
первообразных). Первообразная функции
определяется с точностью до константы,
а точнее выполняются два утверждения:
1) если функция
является первообразной функции
на некотором промежутке
,
то функция
так же является первообразной функции
на данном промежутке для любой константы
С;
2) если
и
– две первообразные функции
на промежутке
,
то их разность является константой:
.
1) Найдем производную функции
:
.
Таким образом,
функция
является первообразной функции
на промежутке
.
2) Найдем производную функции
:
.
По следствию из теоремы Лагранжа (гл.
6) отсюда вытекает, что
.
Множество всех первообразных функции
на некотором промежутке
,
называется неопределенным интегралом
от функции
и обозначается
.
Таким образом,
,
где
– одна из первообразных функции
.
Функция
,
имеющая хотя бы одну первообразную на
промежутке
,
называется функцией, интегрируемой на
промежутке
.
Интегрирование и дифференцирование являются взаимно-обратными операциями, в том смысле, что
-
; -
.
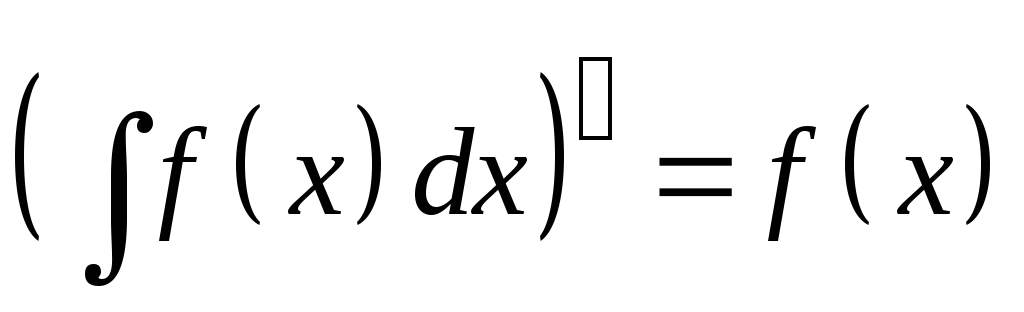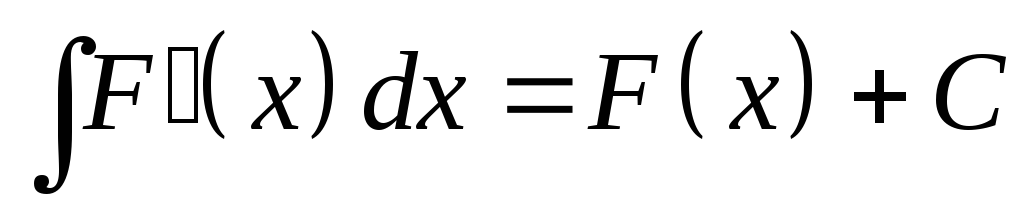(данные свойства проверяются непосредственно).
Два интеграла называются равными на
некотором промежутке
,
если первообразные обеих подынтегральных
функций
соответственно, отличаются не более,
чем на константу:
,
.
Интегралы от наиболее распространенных функций приведены в следующей таблице:
Таблица интегралов
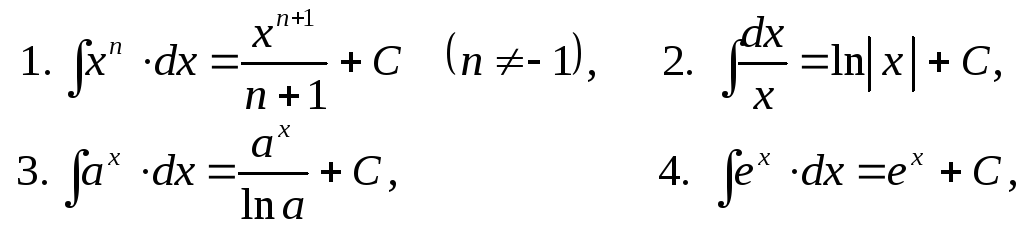
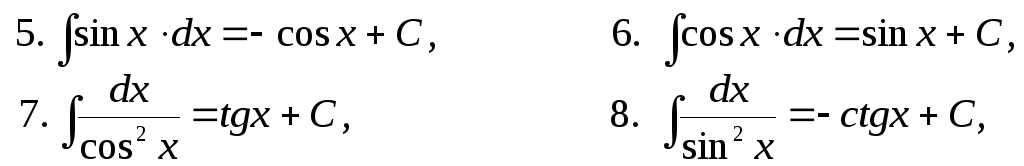
Все табличные формулы можно доказать с помощью дифференцирования. Докажем некоторые из них:
.
Найдем производную
.
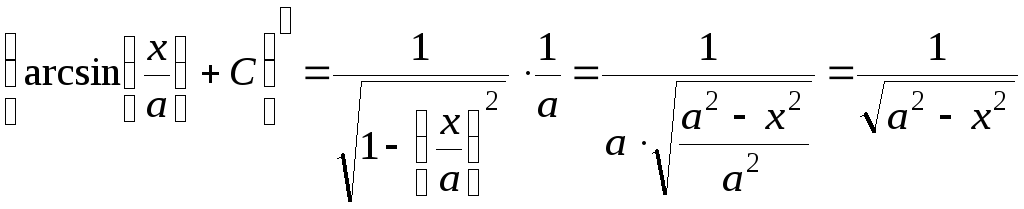Мы получили подынтегральную функцию.
.
1) Найдем производную функции
в том случае, когда выражение
:
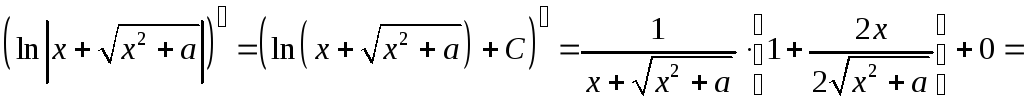
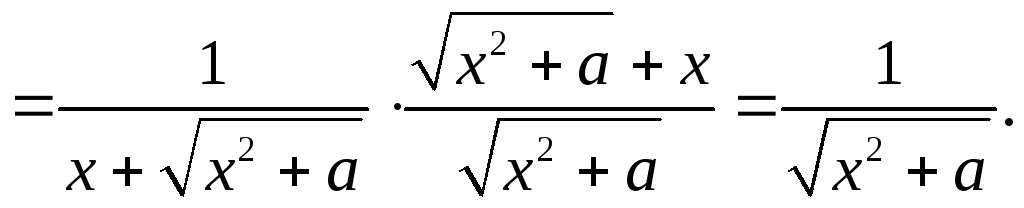
2) Пусть теперь
.
Тогда:
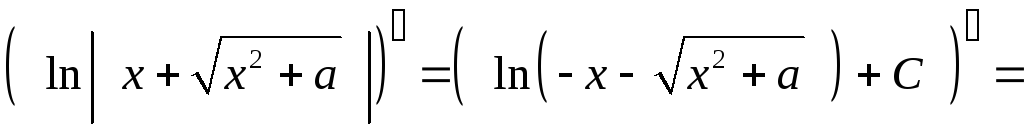
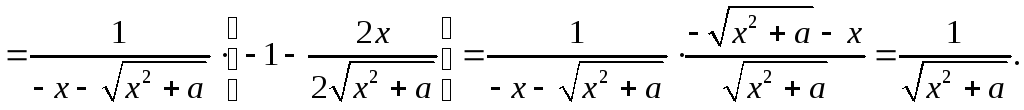
В обоих случаях мы получили подынтегральную функцию.
Свойства неопределенного интеграла
1. Пусть функция
,
является интегрируемой на промежутке
и – некоторая
константа, отличная от нуля. Тогда
постоянный множитель можно выносить
за знак интеграла:
,
(7.1)
Обозначим через
– одну из первообразных функции
на промежутке
.
Тогда
и
,
(7.2)
где
произвольная
константа.
Очевидно, что функция
является интегрируемой на промежутке
,
и в качестве одной из ее первообразных
можно взять функцию
.
Действительно,
.
Следовательно
,
(7.3)
где
произвольная
константа. Сравнивая равенства
(7.2) и (7.3), мы приходим к выводу, о
равенстве интегралов:
,
.
2. Пусть функции
интегрируемы на промежутке
.
Тогда на промежутке
интеграл от суммы данных
функций равен сумме интегралов:
(7.4)
Обозначим через
– произвольную первообразную функции
,
а через
– произвольную первообразную функции
на промежутке
.
Тогда
и
.
Т.е.
,
(7.4)
где
Очевидно, что функия
является первообразной суммы
.
Действительно,
.
Следовательно,
(7.5)
Сравнивая
равенства (7.4) и (7.5), мы убеждаемся в
том, что
.