§6.3. Направление выпуклости и точки перегиба графика функции

Пусть функция y = f(x) дифференцируема на интервале (a; b). Тогда существует касательная к графику функции в любой точке A(x; f(x)) (x(a; b)), причем эта касательная не параллельна оси OY.

 График дифференцируемой на интервале (a; b) функции y = f(x) называется выпуклым вверх (выпуклым), если он расположен не выше любой касательной, проведенной к графику на интервале (a; b) (рис. 6.3).

 График дифференцируемой на интервале (a; b) функции y = f(x) называется выпуклым вниз (вогнутым), если он расположен не ниже любой касательной, проведенной к графику на интервале (a; b) (рис. 6.4).

Рис. 6.3. Рис. 6.4.

 Точки, отделяющие выпуклую часть графика функции от вогнутой (или наоборот), называются точками перегиба графика функции.

 Если функция y = f(x) имеет на интервале (a; b) вторую производную, причем f(x)   (f(x) < ), то во всех точках интервала (a; b) график функции является вогнутым (выпуклым).

 Необходимое условие перегиба графика функции. Пусть график функции y = f(x) в точке М(x₀; f(x₀)) имеет перегиб, и пусть функция y = f(x) имеет в точке x₀ непрерывную вторую производную. Тогда .

Предположим противное, т.е. что . Тогда в силу непрерывности второй производной существует такая окрестность точки x₀, в которой вторая производная имеет тот же знак, что и в точке x₀. Следовательно, в этой окрестности график функции сохраняет направление выпуклости. Таким образом, в точке x₀ график не имеет перегиба. 

Замечание. Необходимое условие не является достаточным условием перегиба графика функции. В качестве простейшего примера можно привести функцию . Вторая производная данной функции обращается в ноль в точке x = 0, однако в этой точке график функции перегиба не имеет (очевидно, что в точке x = 0 функция имеет минимум).

 Точки x₀, в которых выполнено условие , называются критическим точками второго рода.

Точки перегиба графика функции находятся из числа критических точек второго рода. Достаточным условием перегиба графика функции является следующая очевидная теорема.

 Достаточное условие перегиба графика функции. Пусть существует такая -окрестность точки x₀, в которой функция y = f(x) имеет непрерывную вторую производную f(x), принимающую значения разных знаков в интервалах и (т.е. при переходе через точку x₀ вторая производная меняет знак). Тогда в точке x₀ график функции f(x) имеет перегиб.

 Замечание. Достаточное условие перегиба остается верным в том случае, когда в самой точке x₀ вторая производная не существует, но при этом в точке М(x₀; f(x₀)) существует касательная к графику функции y= f(x).

Пример 6.3. Определить участки выпуклости, вогнутости и точки перегиба графика функции .

Решение. Первая производная данной функции была найдена ранее (пример 6.2). Найдем вторую производную данной функции и определим критические точки второго рода.

.

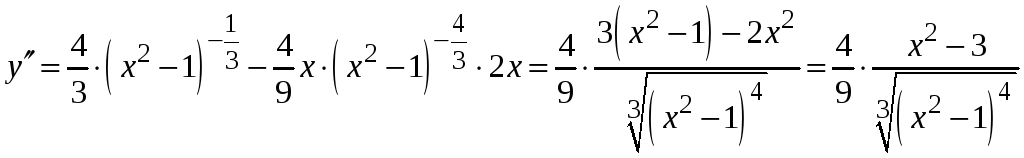Критическими точками второго рода данной функции являются точки , в которых вторая производная данной функции обращается в 0, и точки , в которых вторая производная не существует. Исследуем знак второй производной (рис. 6.5) учитывая, что знаменатель дроби положителен при всех .

Рис. 6.5.

На интервалах , и вторая производная меньше нуля, следовательно, график функции является выпуклым. На интервалах и вторая производная больше нуля, следовательно, график функции является вогнутым. В точках вторая производная меняет знак, следовательно, график функции в этих точках имеет перегиб . В точках вторая производная знака не меняет, следовательно, в этих точках перегиба нет (в примере 6.2 было установлено, что в точках функция имеет минимум). График функции, рассмотренной в примерах 6.2 и 6.3, изображен на рис. 6.6.

Рис. 6.6.