§8.2. Свойства определенного интеграла. Формула Ньютона-Лейбница

Перечислим без доказательства основные свойства определенного интеграла от непрерывной на отрезке [a; b] функции f(x).

1. Постоянный множитель можно выносить за знак определенного интеграла:

. (8.4)

2. Определенный интеграл от суммы двух (или нескольких) функций равен сумме интегралов от этих функций:

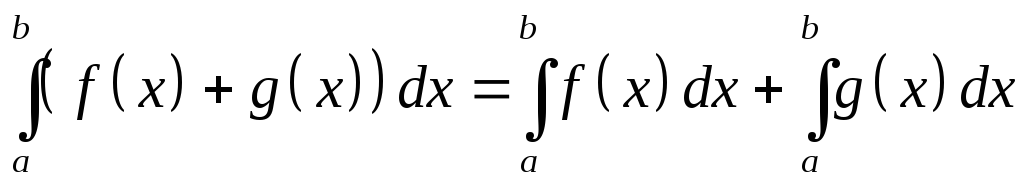. (8.5)

3. Пусть с – произвольная точка из промежутка [a; b], тогда:

. (8.6)

4. При изменении порядка интегрирования, определенный интеграл меняет знак на противоположный:

. (8.7)

5. Теорема о среднем значении. На промежутке [a; b] существует такая точка с, что

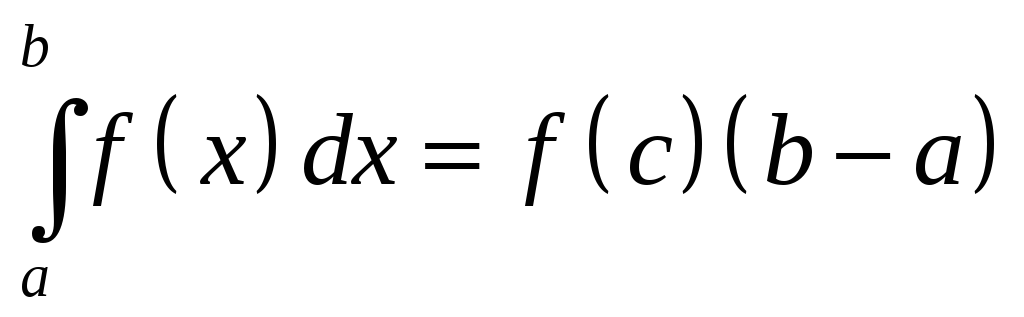. (8.8)

6. Оценка определенного интеграла

. (8.9)

При доказательстве этих и других свойств используется определение определенного интеграла (формула (8.2)), однако, при решении практических задач пользоваться определением определенного интеграла крайне затруднительно. Обычно в таких случаях применяется формула Ньютона-Лейбница в сочетании со свойствами определенного интеграла, или приближенные методы.

 Формула Ньютона-Лейбница:

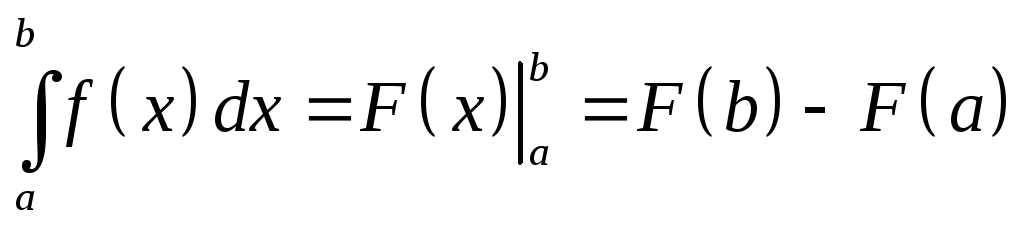. (8.10)

Здесь через F(x) обозначена первообразная функции f(x) на промежутке [a; b]. Если функция f(x) непрерывна на промежутке [a; b], то она интегрируема на [a; b] и, следовательно имеет первообразную.

Пример 8.1. Вычислить определенный интеграл: .

Решение.

.

При вычислении данного интеграла, мы воспользовались 1-м и 2-м свойствами определенного интеграла и формулой Ньютона-Лейбница.

Пример 8.2. Вычислить определенный интеграл: .

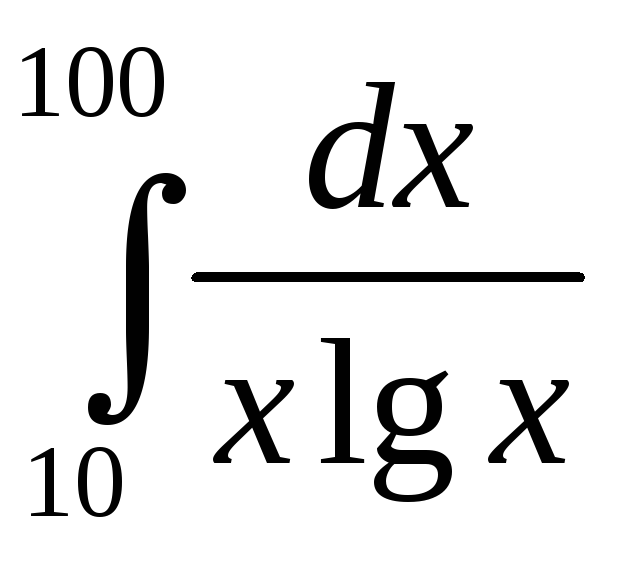Решение. Умножим и разделим подынтегральную функцию на ln10 и внесем множитель под знак дифференциала:

.

§8.3. Замена переменной и интегрирование по частям под знаком определенного интеграла

 Замена переменной под знаком определенного интеграла отличается от изученной ранее замены переменной под знаком неопределенного интеграла двумя обстоятельствами:

1. В ходе замены переменной необходимо изменить пределы интегрирования. Так, если старыми пределами интегрирования являлись числа x₁ и x₂, и мы осуществили подстановку 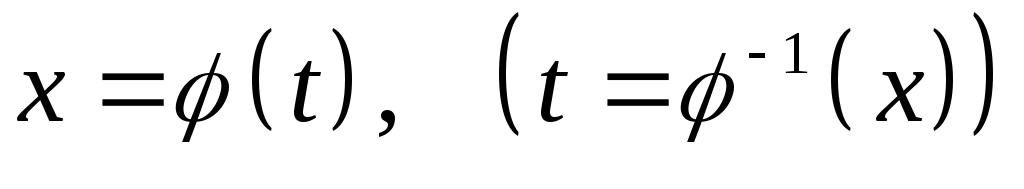, то новыми пределами интегрирования будут числа .

2. После нахождения первообразной 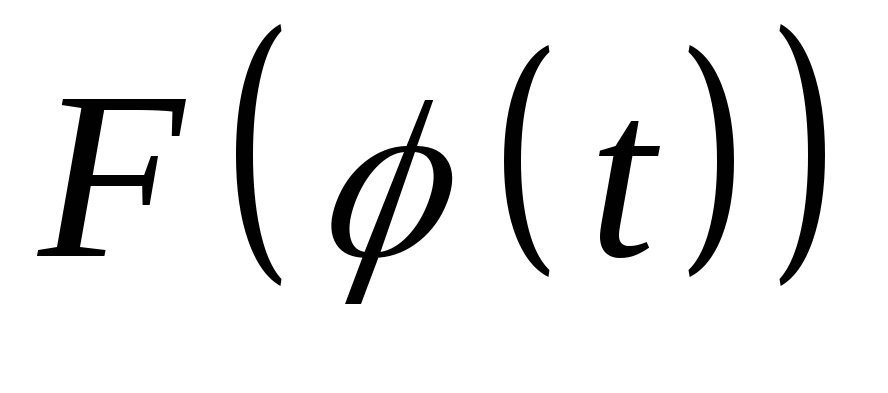нет необходимости возвращаться к старой переменной x, нужно лишь в соответствие с формулой Ньютона-Лейбница подставить в нее новые пределы интегрирования t₁ и t₂: .

Пример 8.3. Вычислить определенный интеграл: .

Решение.

.

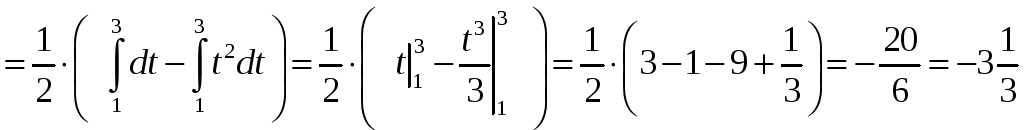 Формула интегрирования по частям в случае определенного интеграла имеет вид:

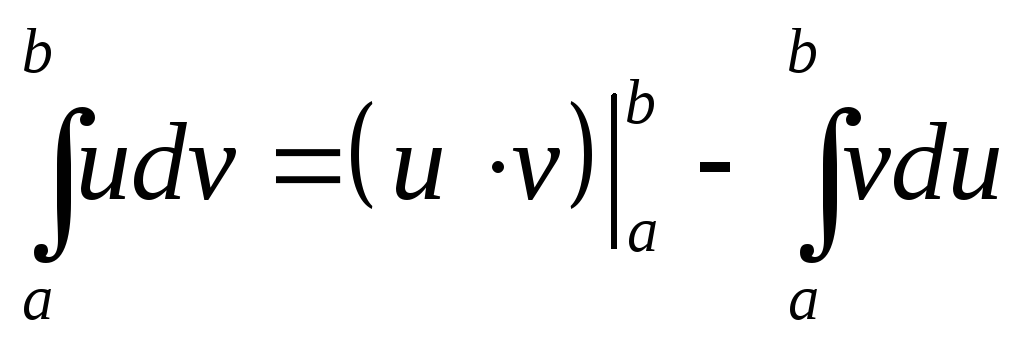. (8.11)

Пример 8.4. Вычислить интеграл: .

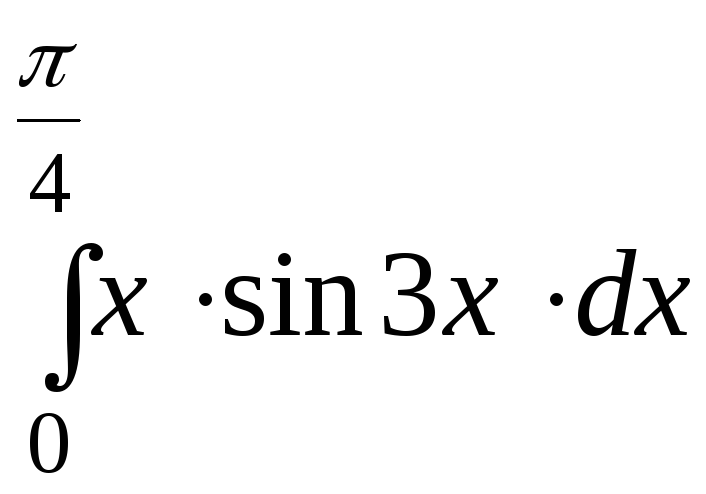Решение.

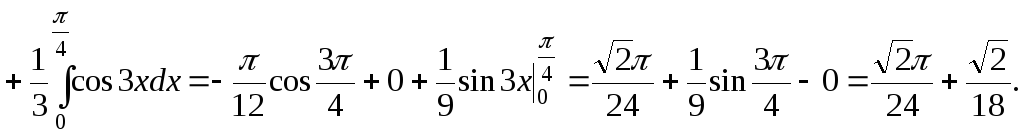
§8.4. Приложения определенных интегралов

1. Вычисление площадей плоских фигур

 Площадь фигуры, ограниченной линиями x = a, x = b, y = f₁(x), y = f₂(x), где f₁(x) и f₂(x) – некоторые непрерывные на отрезке [a; b] функции, причем (рис. 8.2), можно найти по формуле . (8.12)

Рис. 8.2.  Без ограничения общности мож-

но считать, что . В противном случае обе функции можно увеличить на одну и ту же константу (при этом графики обеих функций сместятся вверх) такую, что новые функции окажутся неотрицательными.

Из рисунка 8.2 видно, что искомая площадь равна разности площадей двух криволинейных трапеций . Каждую из площадей S₁ и S₂ можно найти по формуле (8.3). Следовательно

. 

Пример 8.5. Вычислить площадь земельного участка, ограниченного линиями .

Решение. Построим данные линии в декартовой системе координат (рис. 8.3). 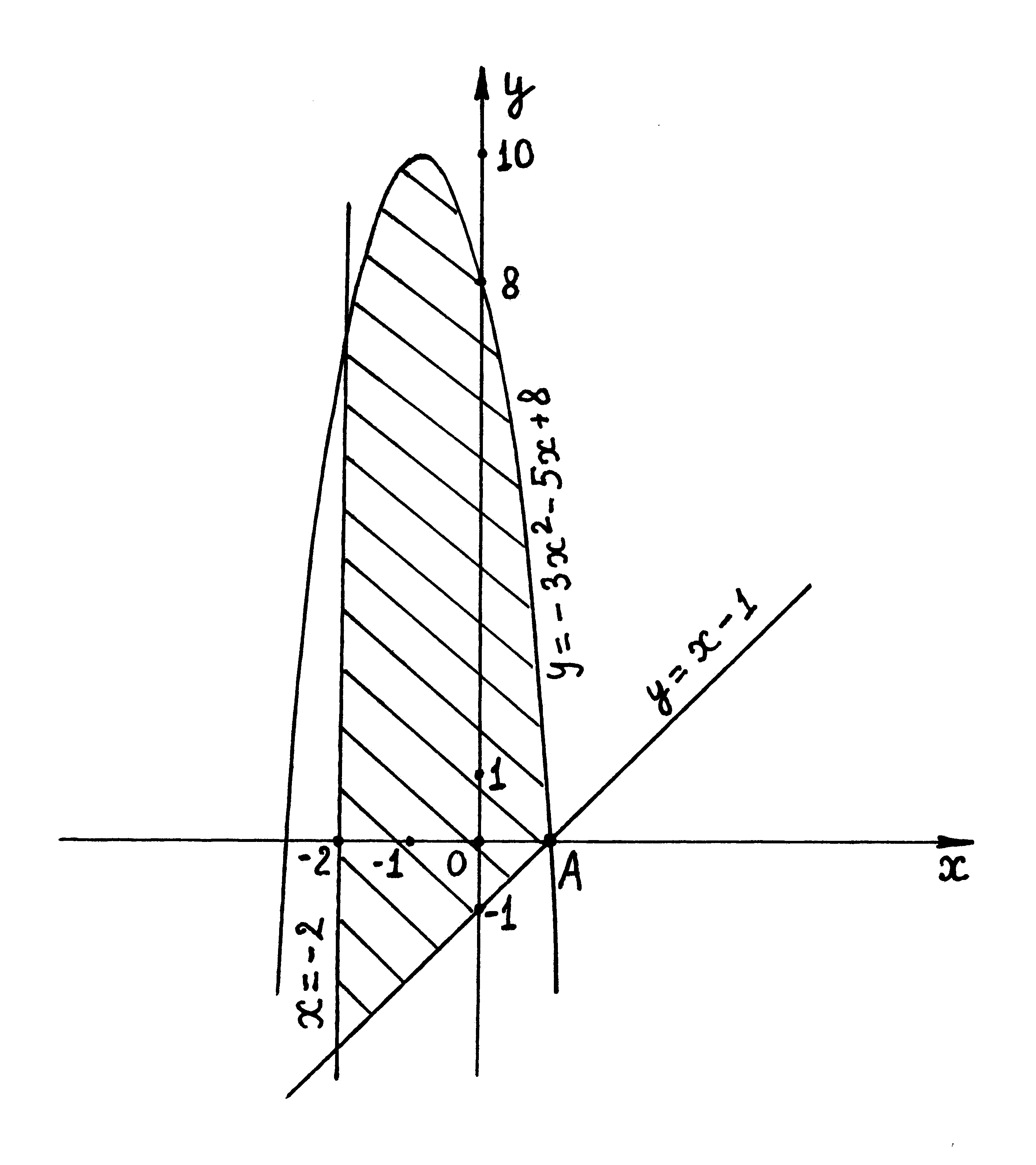Земельный участок изображен заштрихованным. Найдем точку А пересечения параболы с прямой y = x – 1. Для этого решим систему:

.

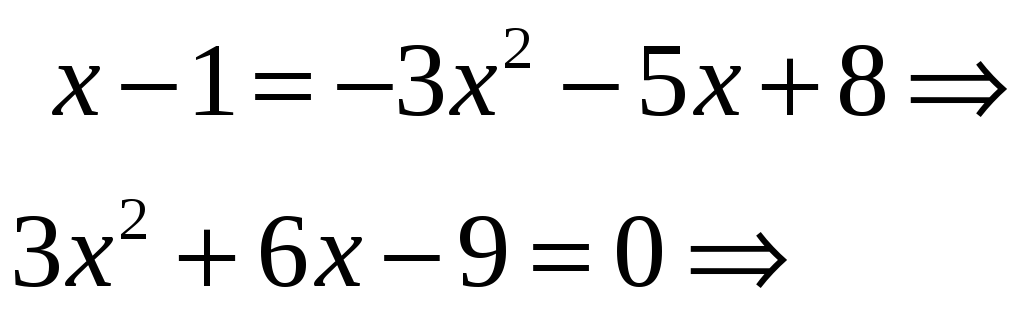
Таким образом,

Рис. 8.3.

Искомую площадь найдем по формуле (8.12):

 Пусть криволинейная трапеция (рис. 8.1) сверху ограничена графиком функции, заданной параметрически 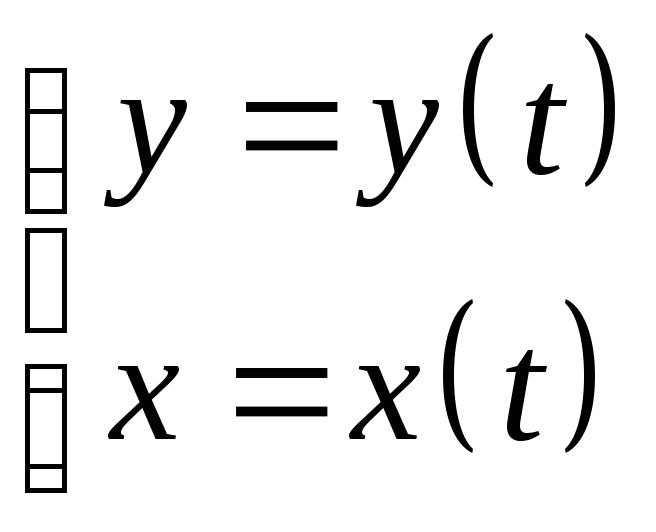на некотором отрезке [t₁; t₂], причем функция y(t) является непрерывной, а функция x(t) – дифференцируемой на данном отрезке. Тогда площадь S криволинейной трапеции находится по формуле:

. (8.13)

Формула (8.13) получена из формулы (8.3), если в последней произвести замену переменной:

.

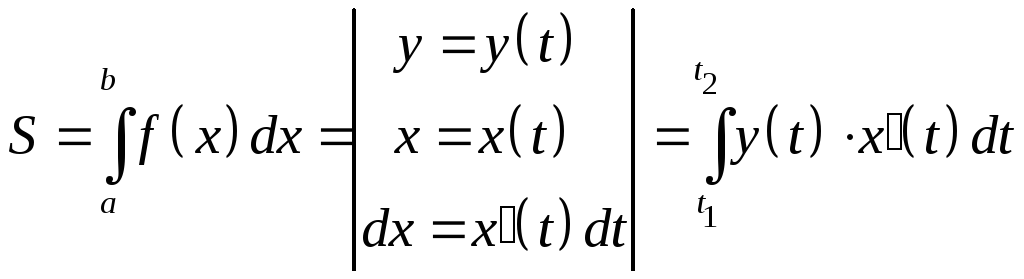Новые пределы интегрирования t₁; и t₂ находятся из систем , . Они соответствуют началу и концу дуги, соответственно.

Пример 8.6. Вычислить площадь, ограниченную первой аркой циклоиды .

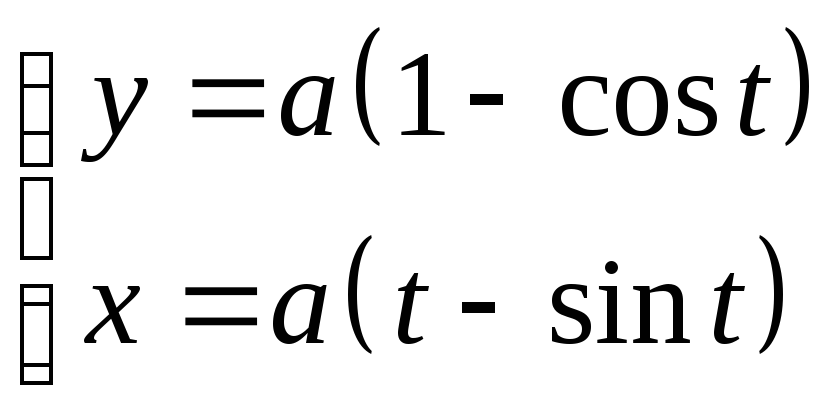Решение. Построим первую арку циклоиду по точкам:

t	0
x	0	0.57a	3.14a	5.71a	6.28a
y	0	a	2a	a	0

Таким образом, началу арки (точ-

Рис 8.4. ке А) соответствует значение параметра t₁ = 0, вершине (точке В) – значение t₂ = , и концу (точке С) – значение t₃ = 2 . Площадь всей арки циклоиды можно найти, вычислив площадь половины арки S₁ (рис. 8.4). По формуле 8.13 получим

.
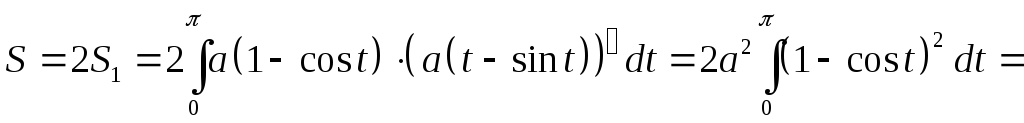
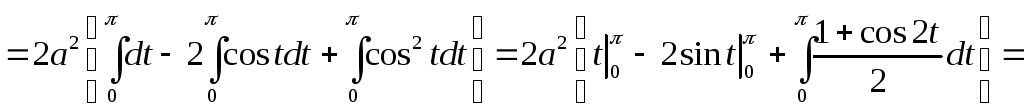
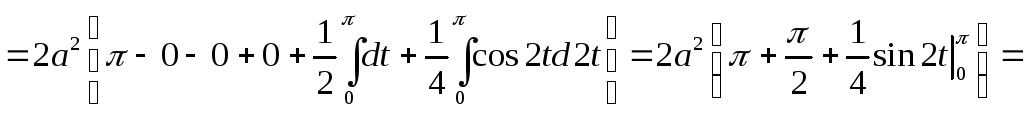