
- •Часть II
- •Введение
- •Глава 6. Полное исследование функции и построение графика
- •§6.1. Экстремум функции. Монотонность
- •§6.2. Исследование функции на экстремум
- •Необходимое условие экстремума
- •Первое достаточное условие экстремума
- •§6.3. Направление выпуклости и точки перегиба графика функции
- •§6.4. Асимптоты графика функции
- •§6.5. Полное исследование функции и построение графика
- •Глава 7. Неопределенный интеграл
- •§7.1. Определение и свойства неопределенного интеграла
- •Свойства неопределенного интеграла
- •§7.2. Табличное интегрирование
- •§7.3. Подведение множителя под знак дифференциала
- •§7.4. Замена переменной под знаком неопределенного интеграла
- •§7.5. Метод интегрирования по частям
- •§7.6. Интегрирование выражений, содержащих квадратный трехчлен в знаменателе
- •§7.7. Интегрирование тригонометрических функций
- •Глава 8. Определенный интеграл.
- •§8.1. Задача о площади криволинейной трапеции. Определение определенного интеграла
- •§8.2. Свойства определенного интеграла. Формула Ньютона-Лейбница
- •§8.3. Замена переменной и интегрирование по частям под знаком определенного интеграла
- •§8.4. Приложения определенных интегралов
- •Вычисление площадей плоских фигур
- •Вычисление длины дуги плоской кривой
- •Вычисление объема тела с известным поперечным сечением.
- •Вычисление объема тела вращения
- •§8.5. Несобственные интегралы
- •Глава 9. Функции нескольких переменных
- •§9.1. Область определения функции нескольких переменных. Непрерывность
- •§9.2. Линии уровня функции двух переменных
- •§9.3. Частные производные первого порядка
- •§9.4. Градиент функции нескольких переменных. Производная по направлению
- •§9.5. Дифференциал функции нескольких переменных и его применение к приближенным вычислениям
- •§9.6. Частные производные высших порядков
- •§9.7. Экстремум функции двух переменных
- •Глава 10. Дифференциальные уравнения
- •§10.1. Дифференциальные уравнения первого порядка
- •1. Дифференциальные уравнения с разделяющимися переменными
- •2. Однородные дифференциальные уравнения 1-го порядка
- •3. Линейные дифференциальные уравнения 1-го порядка
- •§10.2. Простейшие случаи понижения порядка дифференциального уравнения
- •1. Дифференциальные уравнения вида .
- •2. Дифференциальные уравнения вида .
- •3. Дифференциальные уравнения вида .
- •§10.3. Линейные дифференциальные уравненния второго порядка с постоянными коэффициентами
- •Литература
§9.5. Дифференциал функции нескольких переменных и его применение к приближенным вычислениям
Если в точке
![]() функция
функция
![]() имеет непрерывные частные производные
имеет непрерывные частные производные
![]() и
и
![]() ,
то ее полное приращение при переходе
от точки М0 к точке
,
то ее полное приращение при переходе
от точки М0 к точке
![]() может быть представлено в виде:
может быть представлено в виде:
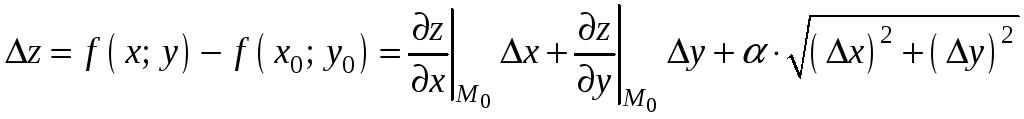 , (9.8)
, (9.8)
где
![]() при
при
![]() ,
,
![]() .
.
Выражение
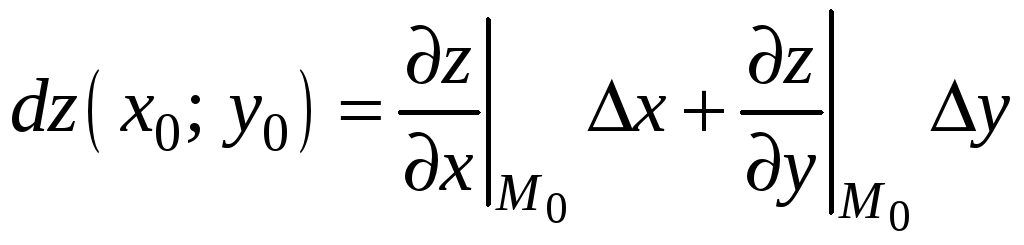 называется полным дифференциалом
функции
называется полным дифференциалом
функции
![]() .
.
Из формулы (9.8) следует, что
дифференциал функции является главной
линейной частью полного приращения
функции
![]() .
При достаточно млых x
и y
выражение
.
При достаточно млых x
и y
выражение
![]() существенно меньше дифференциала и им
можно пренебречь. Такаим образом мы
приходим к следующей приближенной
формуле:
существенно меньше дифференциала и им
можно пренебречь. Такаим образом мы
приходим к следующей приближенной
формуле:
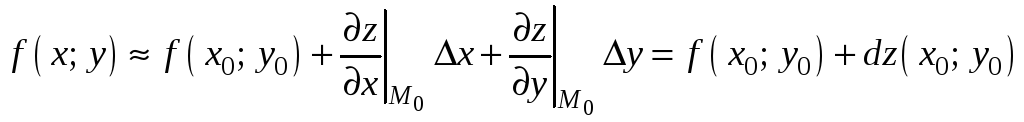 (9.9)
(9.9)
Замечание.
Формулой (9.9) можно пользоваться для
приближенного вычисления значений
функций только в точках
![]() ,
достаточно близких к точке
,
достаточно близких к точке
![]() .
Чем меньше значение
.
Чем меньше значение
![]() ,
тем точнее значение
,
тем точнее значение
![]() ,
найденное по формуле (9.9).
,
найденное по формуле (9.9).
Пример 9.8. Вычислить
![]() приближенно, с помощью дифференциала.
приближенно, с помощью дифференциала.
Решение. Рассмотрим функцию
![]() .
Требуется вычислить значение z1
этой функции в точке (x1;
y1) = (0,09; 6,95).
Воспользуемся приближенной формулой
(9.9), выбрав в качестве точки
.
Требуется вычислить значение z1
этой функции в точке (x1;
y1) = (0,09; 6,95).
Воспользуемся приближенной формулой
(9.9), выбрав в качестве точки
![]() точку (0; 7). Тогда x
= x1
– x0
= 0,09 – 0 = 0,09, y
= y1
– y0
= 6,95 – 7 = – 0,05.
точку (0; 7). Тогда x
= x1
– x0
= 0,09 – 0 = 0,09, y
= y1
– y0
= 6,95 – 7 = – 0,05.
![]() .
.
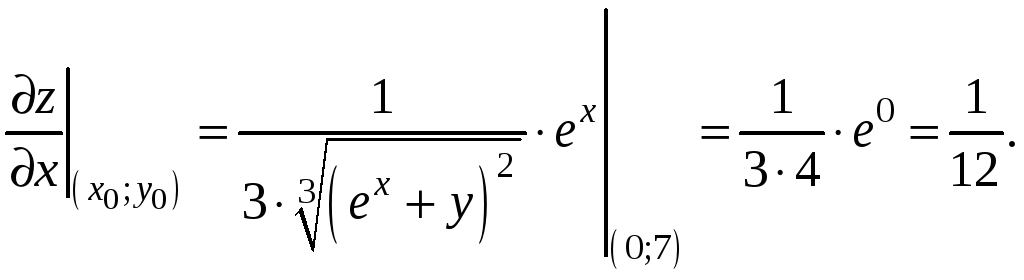
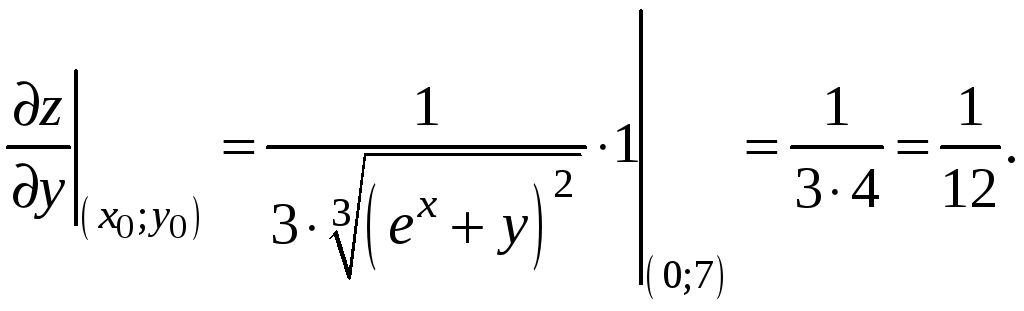
Итак,
![]()
Следовательно,
![]()
§9.6. Частные производные высших порядков
Пусть в области D задана функция
![]() ,
имеющая в этой области непрерывные
частные производные
,
имеющая в этой области непрерывные
частные производные
![]() и
и
![]() .
Таким образом, в области D мы
получили две новые непрерывные функции
двух переменных
.
Таким образом, в области D мы
получили две новые непрерывные функции
двух переменных
![]() и
и
![]() .
Если в некоторой точке
.
Если в некоторой точке
![]() области D функции
области D функции
![]() и
и
![]() имеют частные производные как по
переменной x, так и по переменой
y, то эти производные называются
производными второго порядка функции
имеют частные производные как по
переменной x, так и по переменой
y, то эти производные называются
производными второго порядка функции
![]() .
Они обозначаются следующим образом:
.
Они обозначаются следующим образом:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Если в некоторой точке
![]() области D функция
области D функция
![]() имеет непрерывные смешанные производные
имеет непрерывные смешанные производные
![]() и
и
![]() ,
то в точке
,
то в точке
![]() эти производные равны:
эти производные равны:
![]() .
.
Из данной теоремы следует, что у функции двух переменных, имеющей непрерывные производные второго порядка достаточно найти не четыре, а всего лишь три производные второго порядка.
Пример 9.10. Найти все вторые частные
производные функции
![]() и убедится в том, что смешанные производные
равны
и убедится в том, что смешанные производные
равны
![]() .
.
Решение. 1) Найдем частные производные первого порядка:
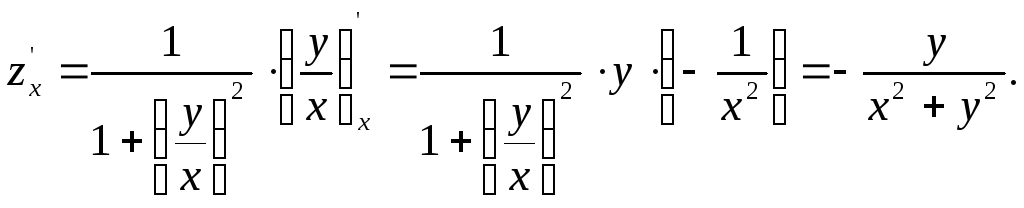
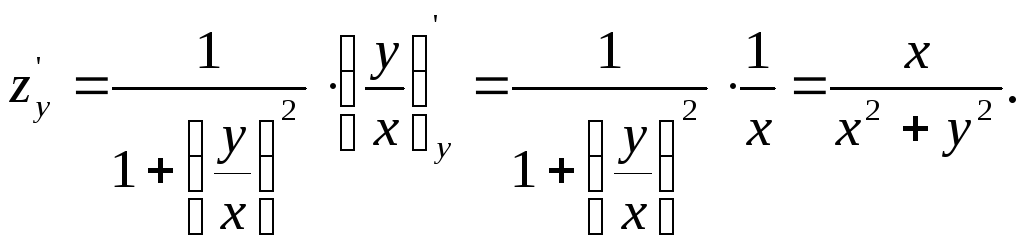
2) Найдем частные производные второго порядка:

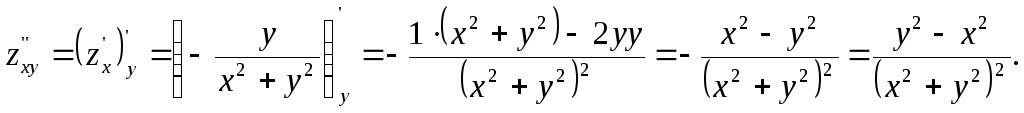

Таким
образом,
![]() .
.
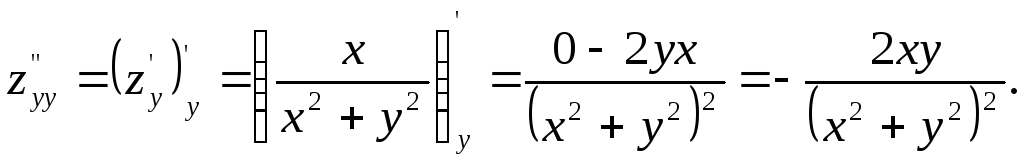
Аналогично тому, как были определены частные производные второго порядка, можно определить частные производные более высоких порядков.
Пример 9.11. Найти частную производную
третьего порядка
![]() функции
функции
![]() .
.
Решение. Последовательно дифференцируя исходную функцию дважды по переменной x, а затем, по переменой y, получим:
![]() ,
,
![]() ,
,
 .
.
§9.7. Экстремум функции двух переменных
Предположим, что в некоторой области
D задана некоторая
непрерывная функция
![]() .
.
Точка
![]() называется точкой максимума (локального
максимума) функции
называется точкой максимума (локального
максимума) функции
![]() ,
если существует такая окрестность U
точки
,
если существует такая окрестность U
точки
![]() ,
целиком лежащая в области D,
во всех точках которой выполнено
неравенство:
,
целиком лежащая в области D,
во всех точках которой выполнено
неравенство:
![]() .
.
Точка
![]() называется точкой минимума (локального
минимума) функции
называется точкой минимума (локального
минимума) функции
![]() ,
если существует такая окрестность U
точки
,
если существует такая окрестность U
точки
![]() ,
целиком лежащая в области D,
во всех точках которой выполнено
неравенство:
,
целиком лежащая в области D,
во всех точках которой выполнено
неравенство:
![]() .
.
Точки максимума и минимума функции
![]() называются точками экстремума.
называются точками экстремума.
Необходимое условие экстремума
функции двух переменных. Пусть в
точке
![]() функция
функция
![]() имеет непрерывные частные производные.
Тогда для того чтобы функция
имеет непрерывные частные производные.
Тогда для того чтобы функция
![]() имела экстремум в точке
имела экстремум в точке
![]() ,
необходимо выполнение условий:
,
необходимо выполнение условий:
 .
(9.10)
.
(9.10)
Если в некоторой точке
![]() выполнены условия (9.10), то точка
выполнены условия (9.10), то точка
![]() называется стационарной (подозрительной
на экстремум) точкой функции
называется стационарной (подозрительной
на экстремум) точкой функции
![]() .
.
Достаточное условие экстремума
функции двух переменных. Пусть в
стационарной точке
![]() функция
функция
![]() имеет непрерывные частные производные
второго порядка
имеет непрерывные частные производные
второго порядка
![]() ,
,
![]() ,
,
![]() .
Обозначим через
.
Обозначим через
![]() – дискриминант функции
– дискриминант функции
![]() в точке
в точке
![]() .
Тогда
.
Тогда
-
если
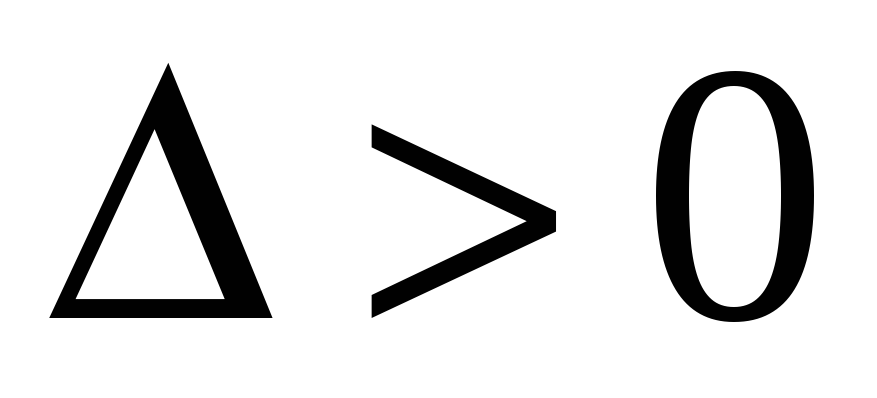 ,
то функция
,
то функция
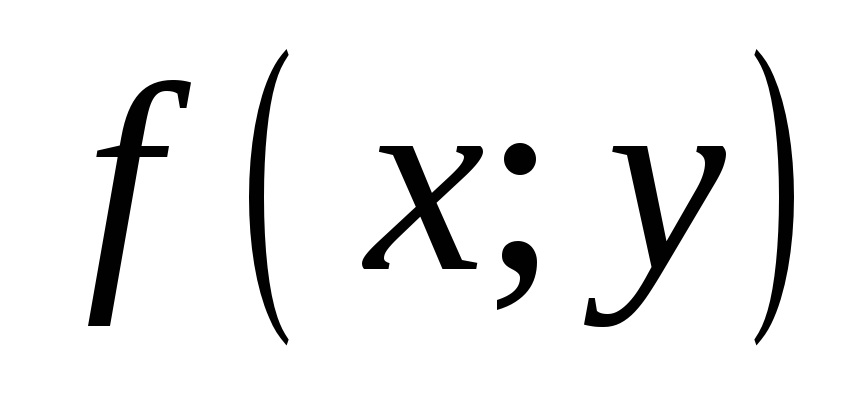 имеет экстремум в точке
имеет экстремум в точке
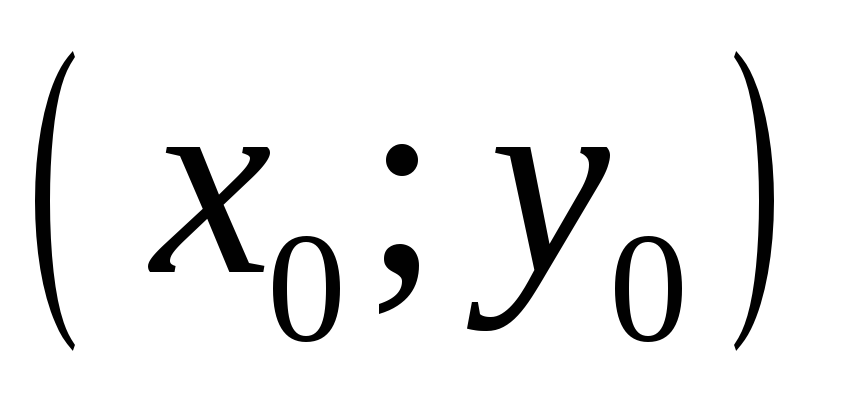 .
А именно максимум, если
.
А именно максимум, если
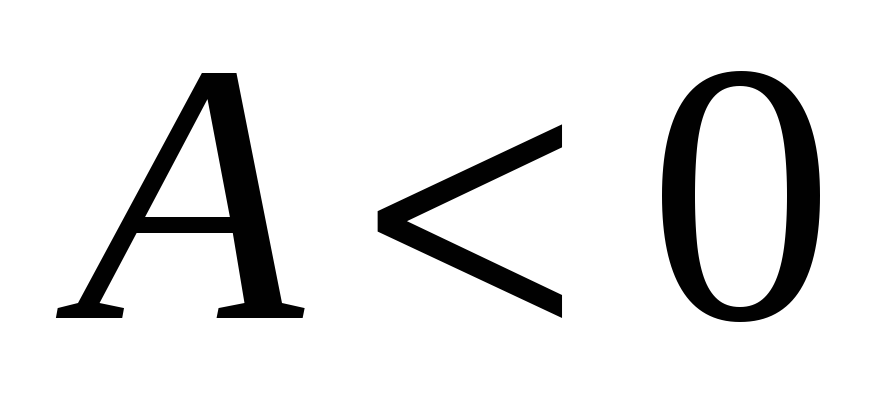 (или
(или
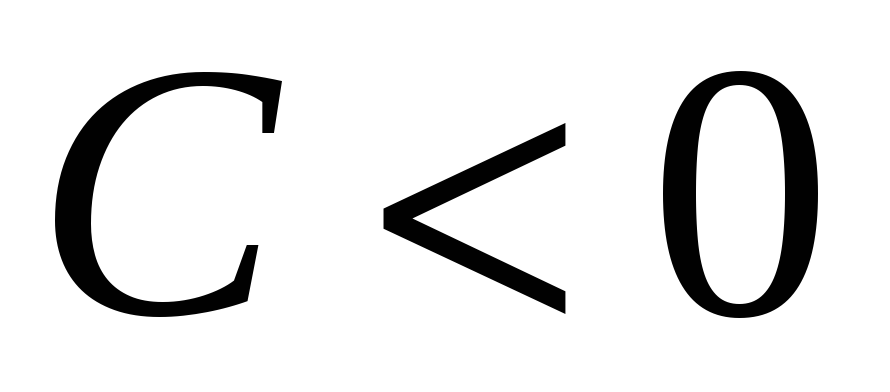 )
и минимум, если
)
и минимум, если
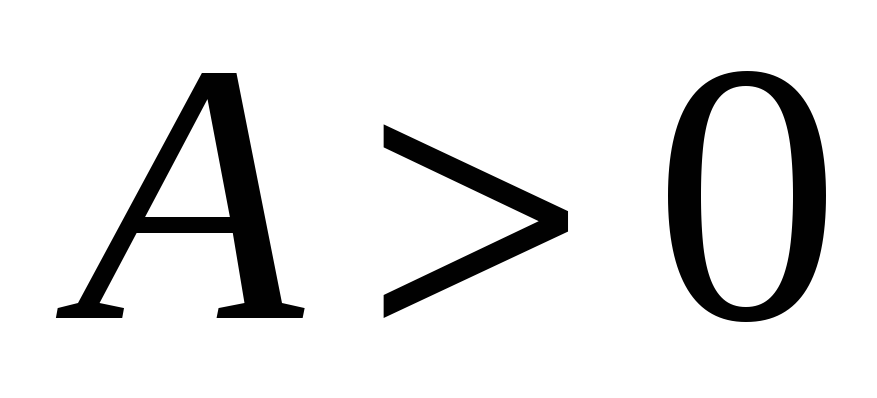 (или
(или
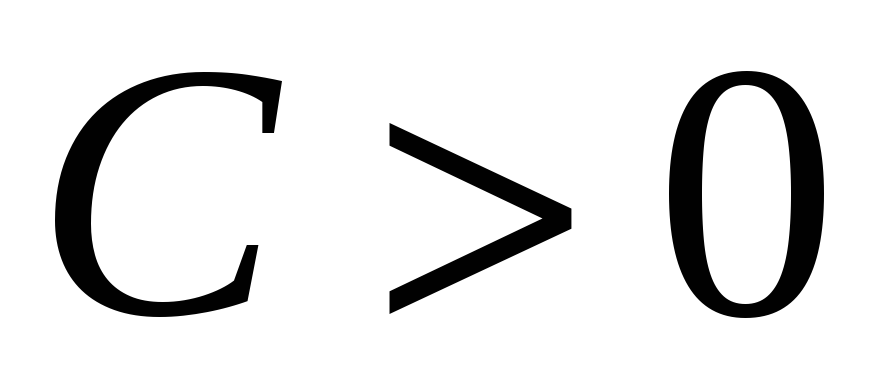 ).
). -
если
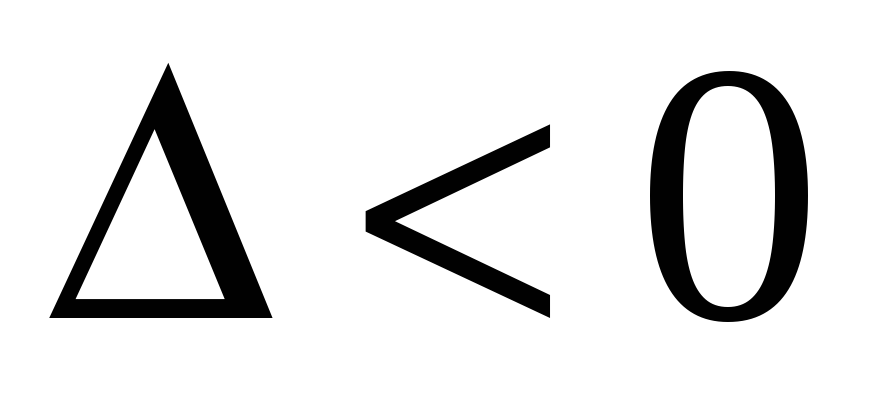 ,
то функция
,
то функция
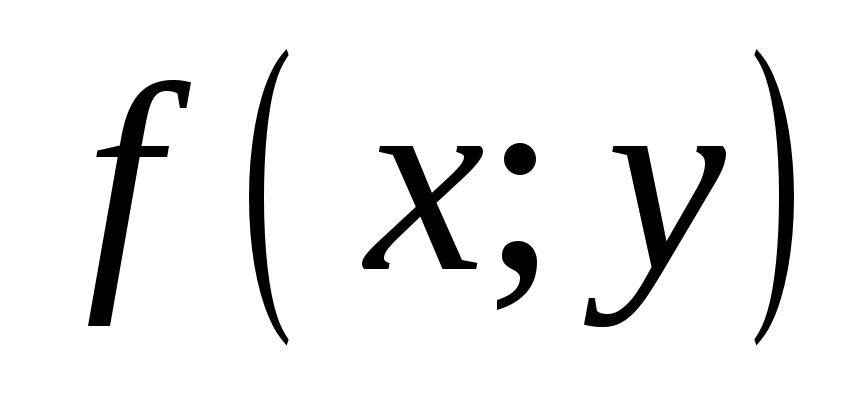 в точке
в точке
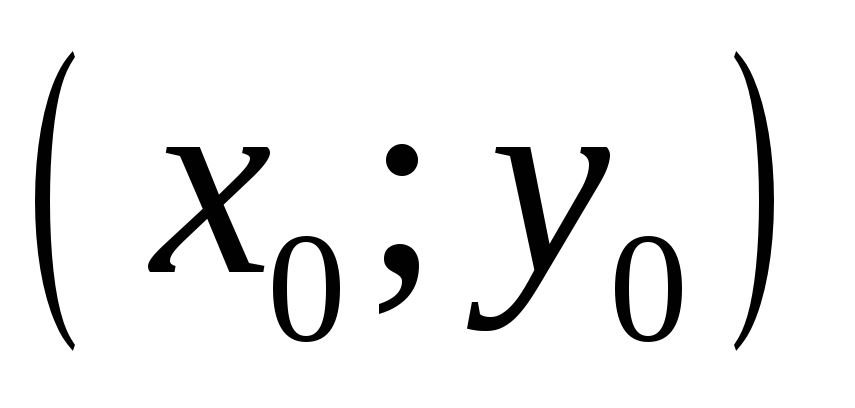 экстремума не имеет.
экстремума не имеет. -
если
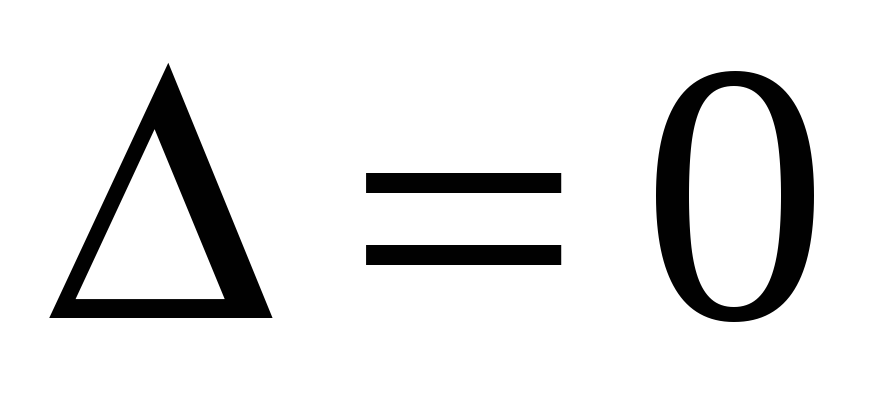 ,
то вопрос о наличии экстремума функции
,
то вопрос о наличии экстремума функции
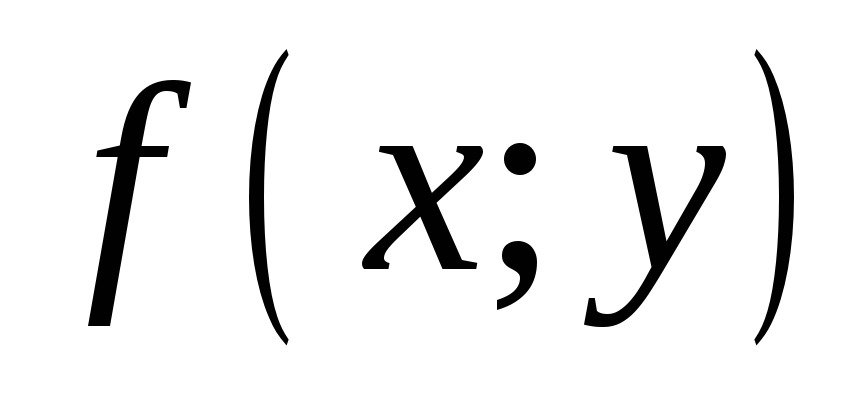 в точке
в точке
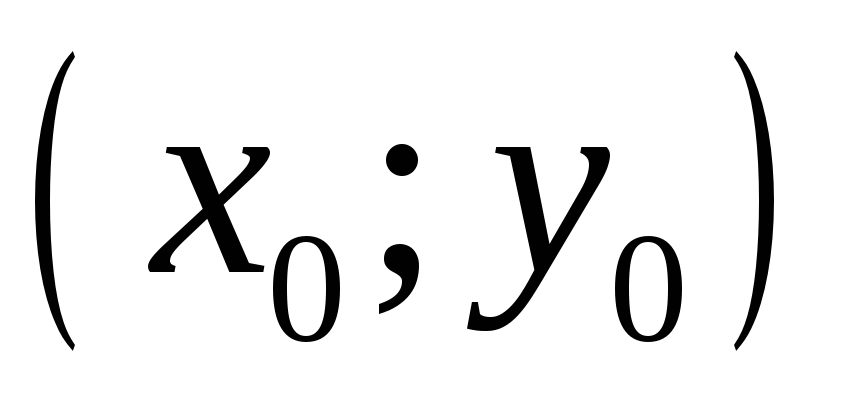 решается с помощью производных более
высокого порядка и формулы Тейлора. В
данном пособии соответствующие
исследования не приводятся.
решается с помощью производных более
высокого порядка и формулы Тейлора. В
данном пособии соответствующие
исследования не приводятся.
Пример
9.12. Найти экстремумы функции
![]() .
.
Решение. Найдем частные производные
первого порядка:
![]() ,
,
![]() .
Приравняем полученные частные производные
к нулю. Получим систему уравнений для
определения точек, подозрительных на
экстремум:
.
Приравняем полученные частные производные
к нулю. Получим систему уравнений для
определения точек, подозрительных на
экстремум:
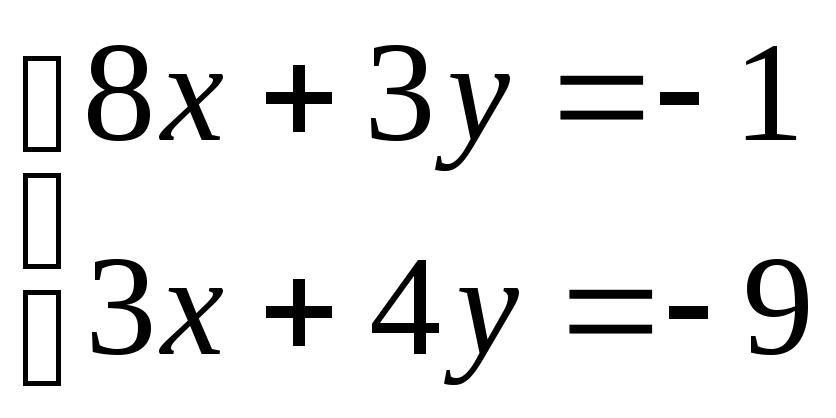 .
Решим данную систему, например, методом
Крамера.
.
Решим данную систему, например, методом
Крамера.
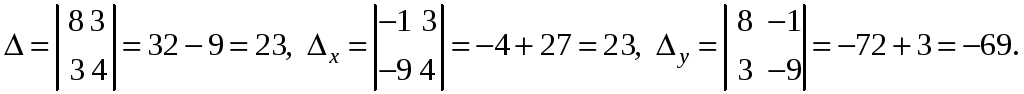
Следовательно,
![]() .
Таким образом, точка М(1; -3) –
является единственной точкой,
подозрительной на экстремум.
.
Таким образом, точка М(1; -3) –
является единственной точкой,
подозрительной на экстремум.
Найдем частные производные второго порядка:
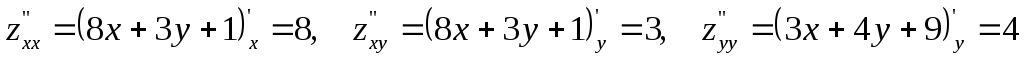 .
.
В точке М
вычислим дискриминант D
по формуле D = AC
– B2, где
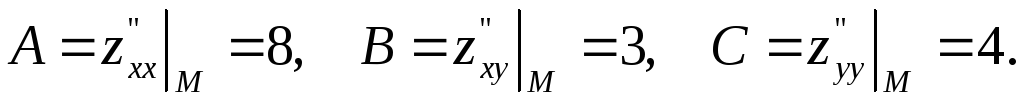 То есть D = 32 – 9 = 23.
То есть D = 32 – 9 = 23.
Так как дискриминант больше нуля, то в точке М функция имеет экстремум. А именно, минимум, поскольку А и С больше нуля. При этом
![]()
