§9.2. Линии уровня функции двух переменных

 Линии на плоскости xOy, заданные уравнениями , где С – произвольная константа, называются линиями уровня функции .

Линии уровня являются линиями пересечения поверхности, заданной функцией и плоскости z = C, параллельной плоскости xOy. С помощью линий уровня можно изучать форму поверхности, заданной функцией .

Пример 9.2. Найти линии уровня и определить форму поверхности, заданной уравнением .

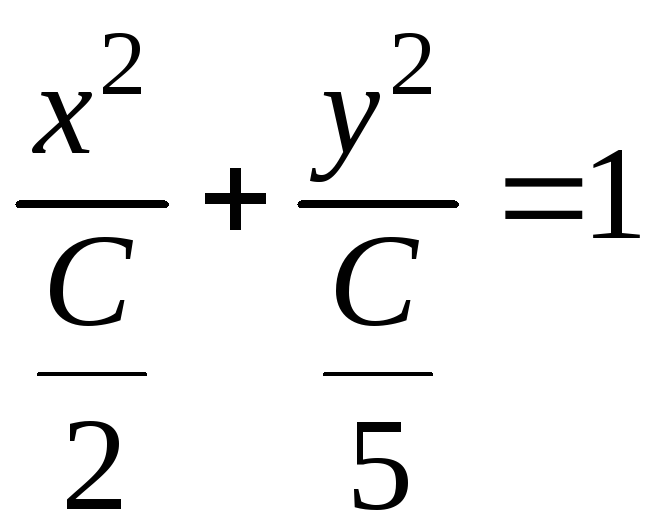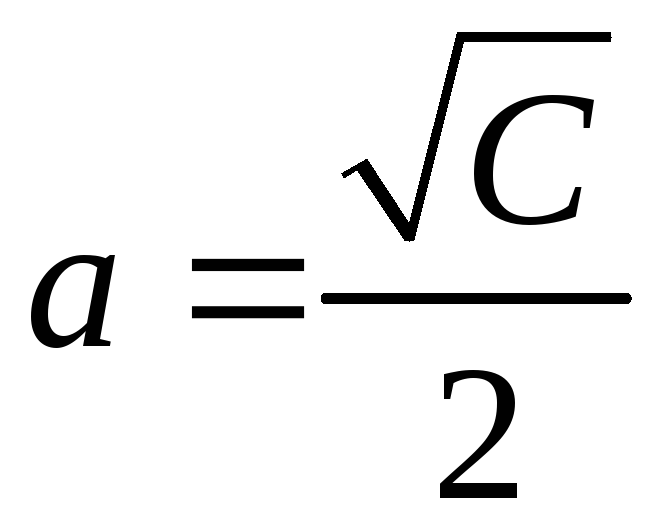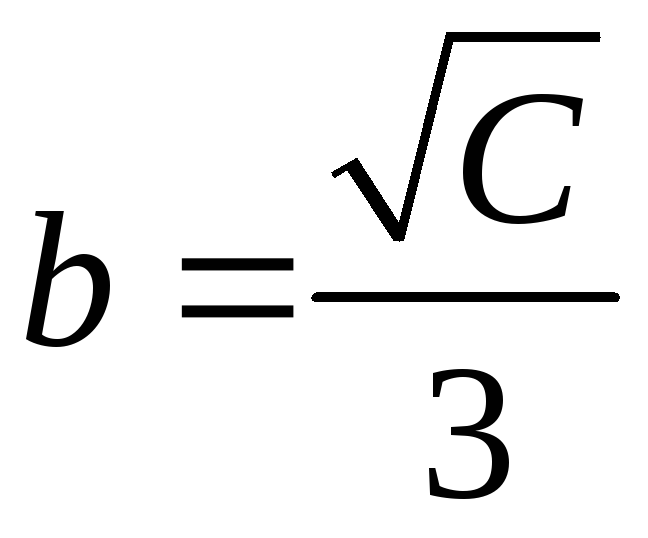Решение. Уравнения линий уровня в данном случае имеют вид . При C < 0 уравнение дает пустое множество решений (следовательно, вся поверхность расположена выше плоскости xOy). При C = 0 уравнению линии уровня удовлетворяет только одна точка x = 0, y = 0 (с плоскостью xOy поверхность пересекается только вначале координат). При C > 0 линии уровня являются эллипсами , с полуосями и . Линии уровня, соответствующие различным значениям С, изображены на рис. 9.3. Поверхность, заданная уравнением , называется эллиптическим параболоидом (рис. 9.4).

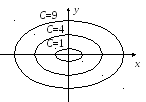
Рис.9.3 Рис. 9.4

§9.3. Частные производные первого порядка

Пусть в некоторой области D плоскости xOy задана функция , и пусть – некоторая точка области D.

 Частной производной функции в точке по переменной x (обозначается или ) называется

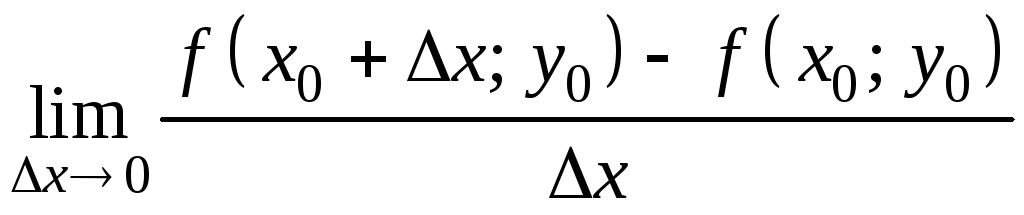, (9.1)

если данный предел существует и конечен.

 Частной производной функции в точке по переменной y (обозначается или ) называется

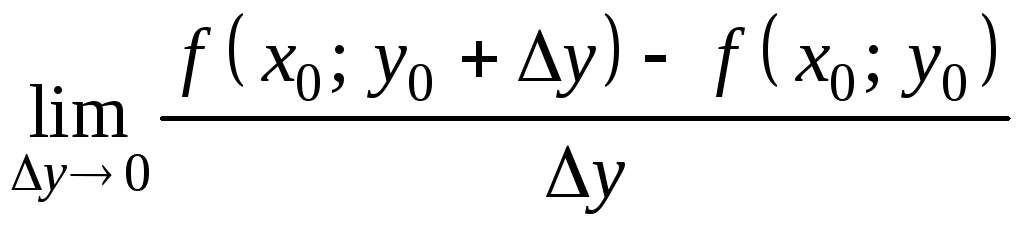, (9.2)

если данный предел существует и конечен.

 Частной производной функции n переменных в точке по переменной x_i называется

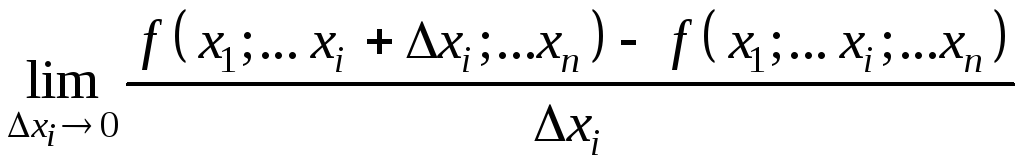, (9.3)

если данный предел существует и конечен.

Как видно из формул (9.1) – (9.3), частные производные определяются аналогично тому, как определялась производная функции одной переменной. При вычислении предела приращение получает только одна из переменных, остальные переменные приращения не получают и остаются постоянными. Следовательно, частные производные можно вычислять по тем же правилам, что и обычные производные, обращаясь со всеми свободными переменными (кроме той, по которой производится дифференцирование) как с константами.

Пример 9.3. Найти частные производные функции

.

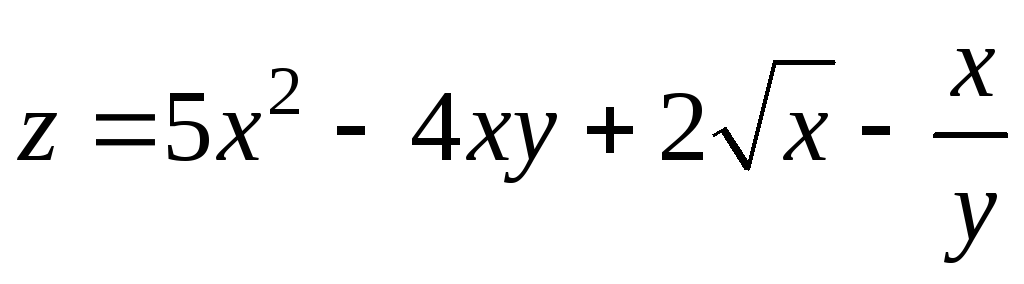Решение. .

.

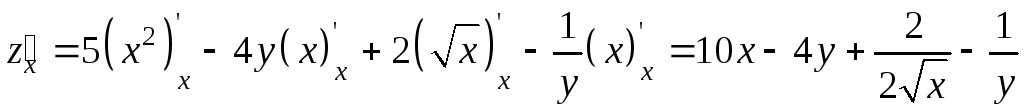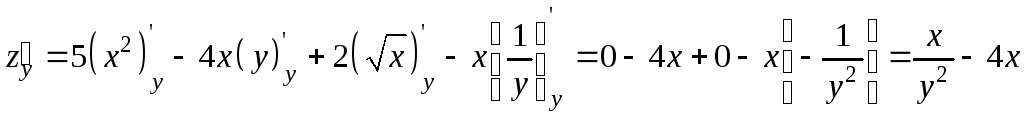Пример 9.4. Найти частные производные функции .

Решение. При дифференцировании данной функции по переменной x мы пользуемся правилом дифференцирования степенной функции, а при нахождении частной производной по переменной y – правилом дифференцирования показательной функции:

,

.

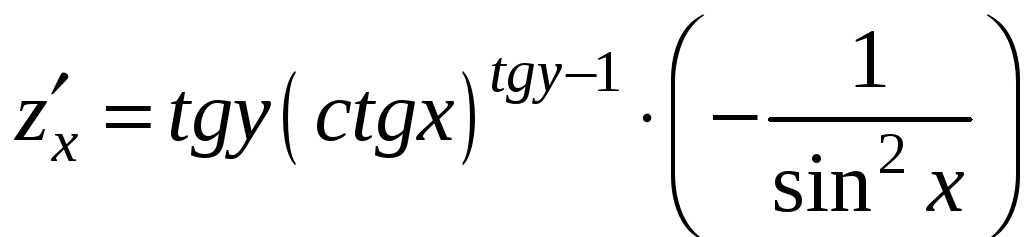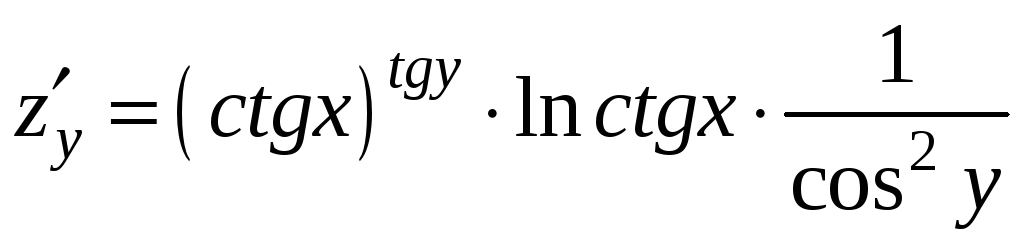Пример 9.5. Вычислить частные производные 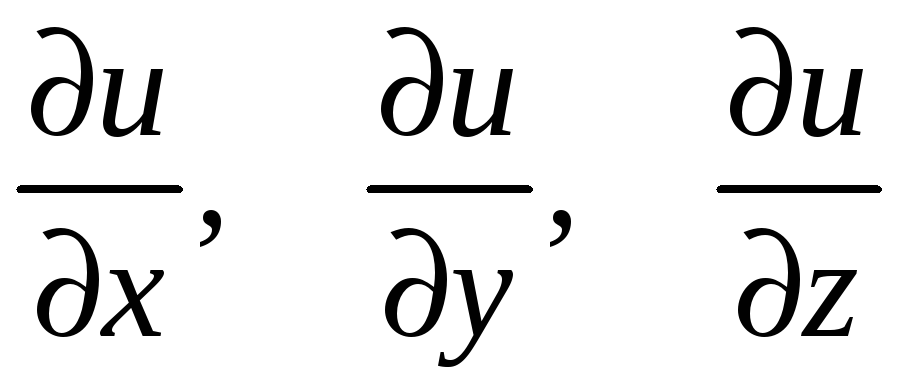функции в точке .

Решение. Применяя правило дифференцирования сложной функции, найдем частные производные

,

,

.

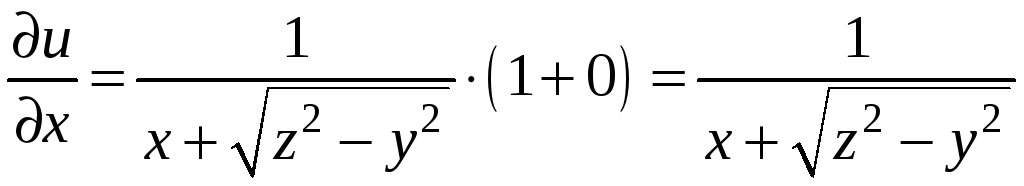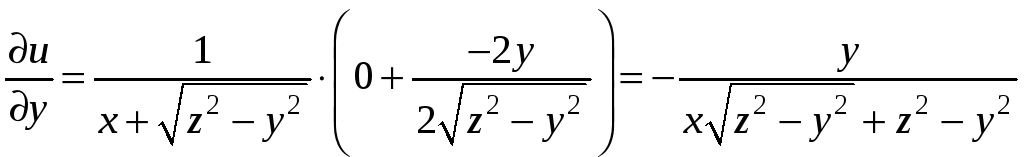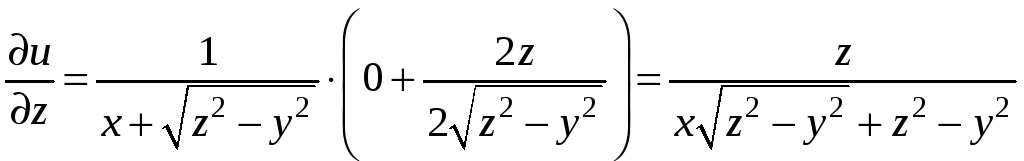Подставляя в частные производные координаты точки М, получим

,

,

.

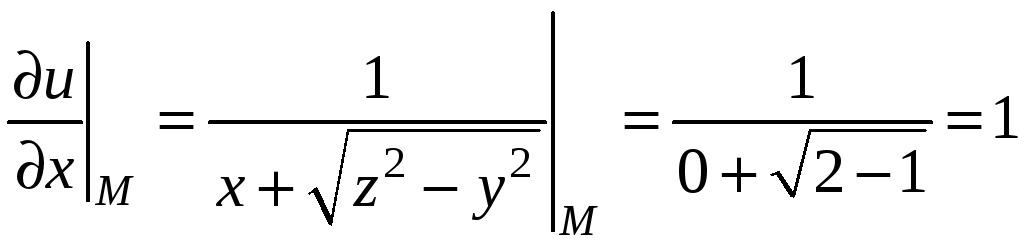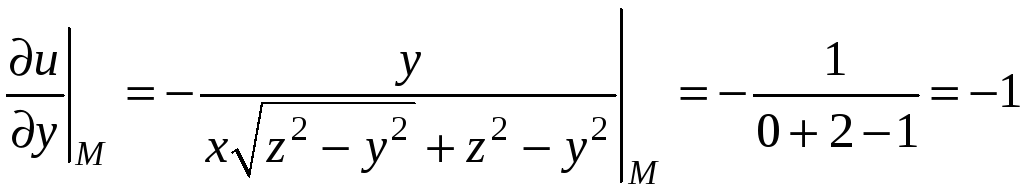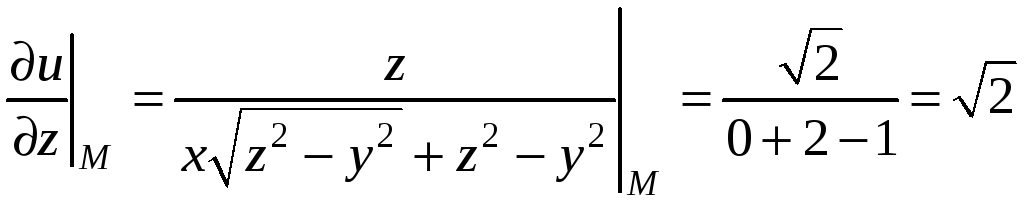§9.4. Градиент функции нескольких переменных. Производная по направлению

 Градиентом функции в точке называется вектор, составленный из частных производных данной функции, вычисленных в данной точке:

. (9.4)

 Если в точке градиент функции отличен от нулевого вектора, то он направлен в сторону наибольшего возрастания данной функции в точке М₀. Это означает, что существует такое достаточно малое число  > 0, что в точке , находящейся от точки на расстоянии r <  (), приращение функции будет максимальным, если направление вектора совпадает с направлением вектора .

 Производной функции в точке по направлению вектора называется проекция вектора градиента данной функции, вычисленного в точке М₀, на данное направление

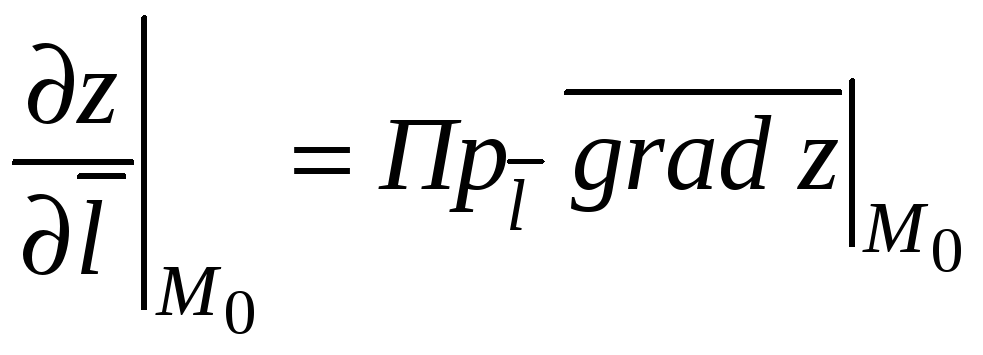. (9.5)

Из формулы (9.5) следует, что по знаку производной по направлению в точке М₀ можно определить поведение функции (возрастание или убывание) в данной точке и в данном направлении. Угол между векторами и острый (функция в данном направлении возрастает), тогда и только тогда, когда производная по направлению вектора в точке М₀ больше нуля. Угол между векторами и тупой (функция в данном направлении убывает), тогда и только тогда, когда производная по направлению вектора в точке М₀ меньше нуля.

Вычисляя проекцию вектора на вектор в соответствие с формулой (2.6) первой части пособия, получим

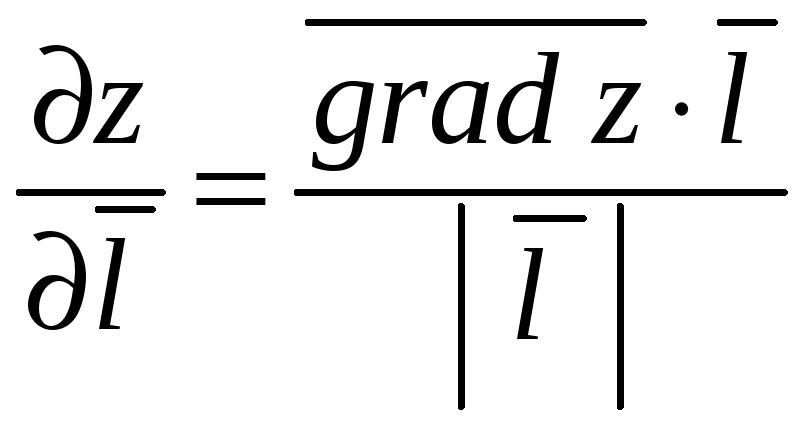. (9.6)

Замечая, что 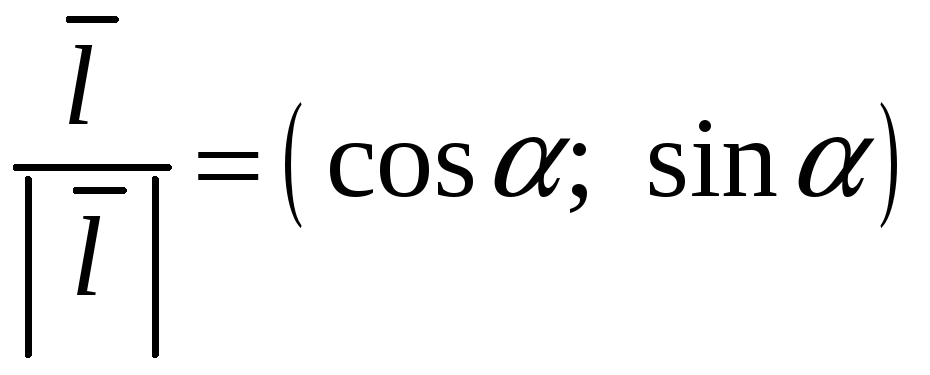, где  – угол, который вектор образует с осью OX, получим еще одну формулу для вычисления производной по направлению вектора

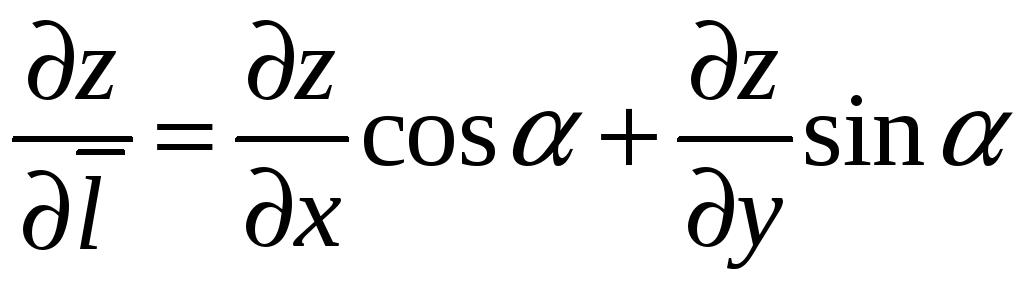. (9.7)

Пример 9.6. Найти градиент функции в точке М₀(4; 2) и производную по направлению вектора

Решение. Найдем частные производные

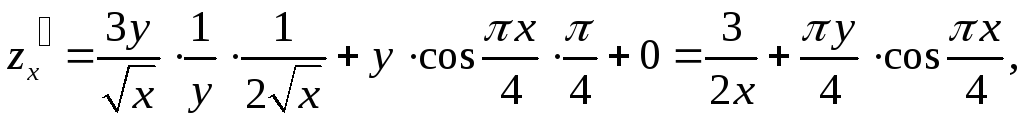
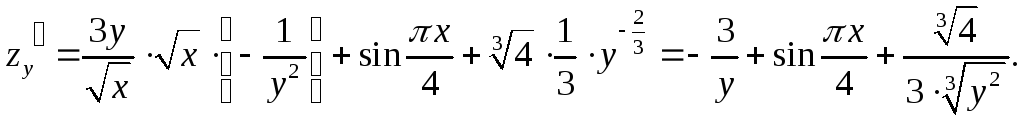
Вычислим значения частных производных в точке М₀:

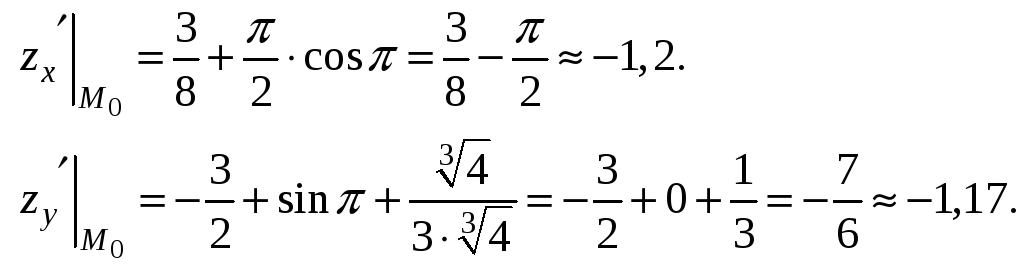
Градиент функции в точке М₀ найдем по формуле (9.4):

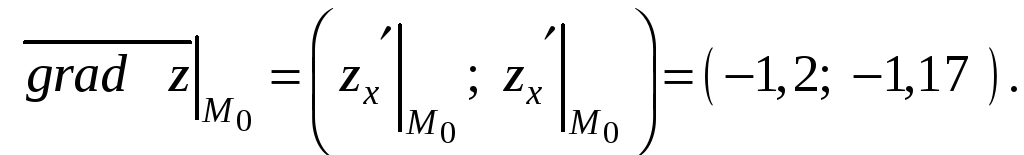
Производную функции в точке М₀ по направлению вектора найдем по формуле (9.6):

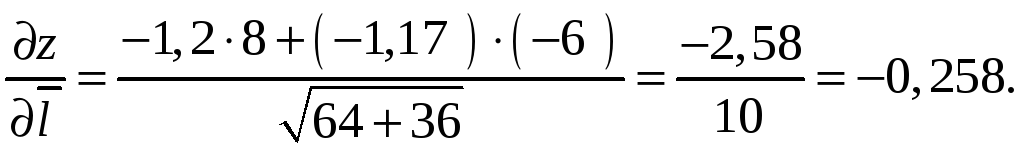
Пример 9.7. В точке М₀(0; 1) вычислить производную функц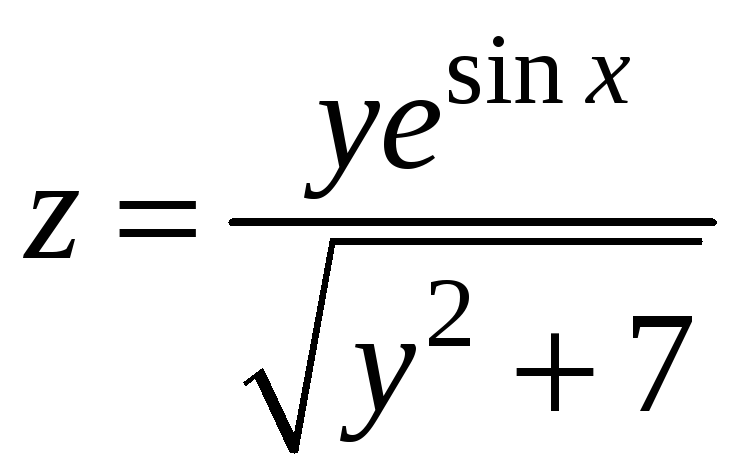ии по направлению биссектрисы второго координатного угла и сделать вывод о поведении функции в данном направлении.

Решение. Найдем частные производные функции :

,

.

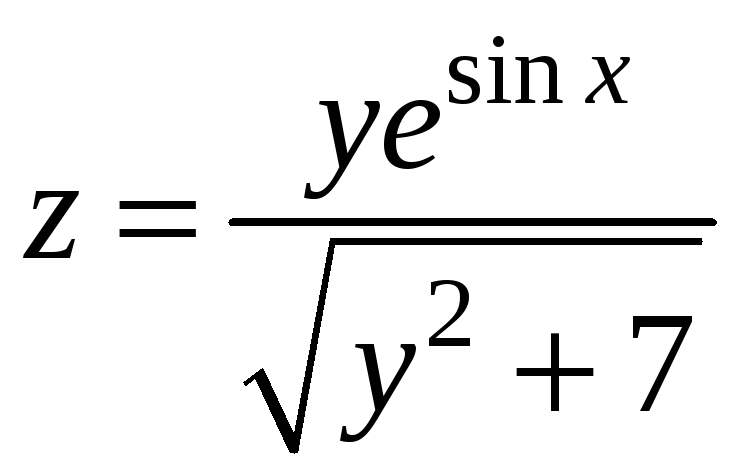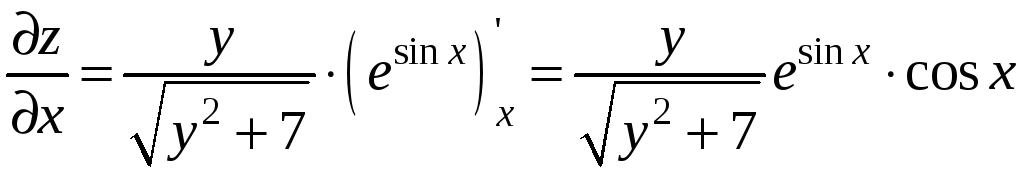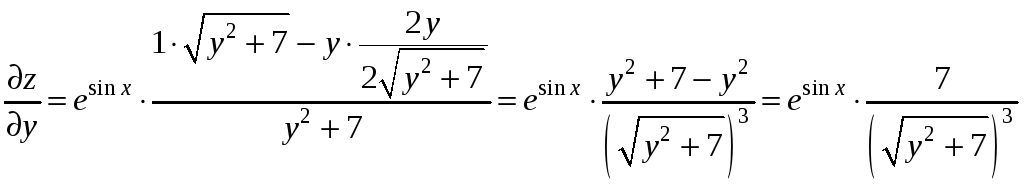Вычислим значения частных производных и градиент функции в точке М₀:

,

,

.

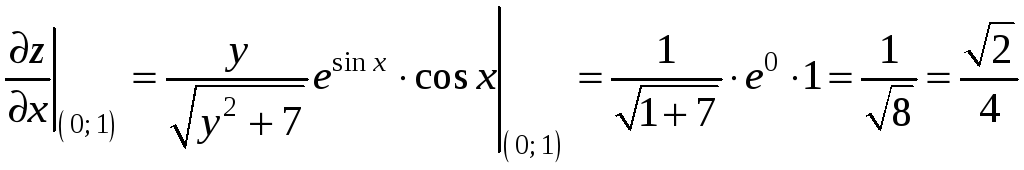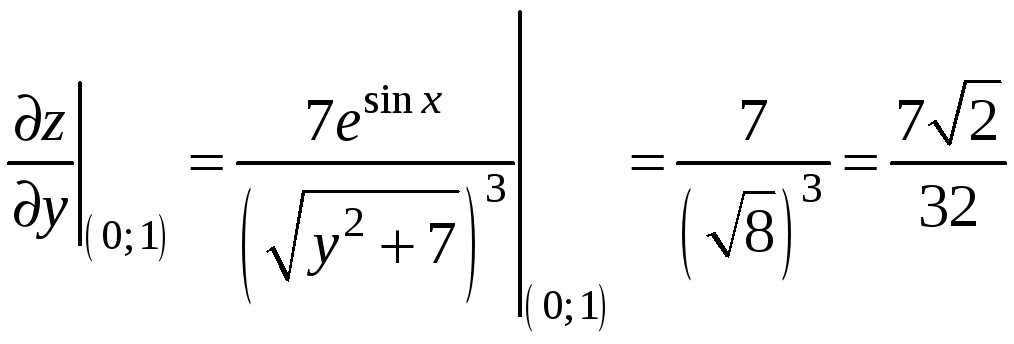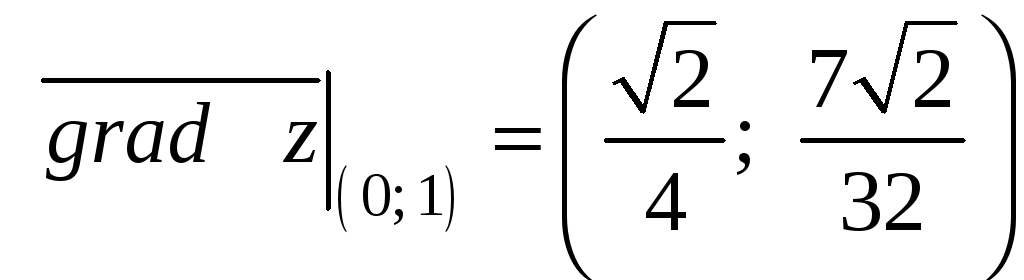Производную функции в точке М₀ по направлению биссектрисы второго координатного угла (данное направление составляет с осью OX угол  = 135) найдем по формуле (9.7):

.

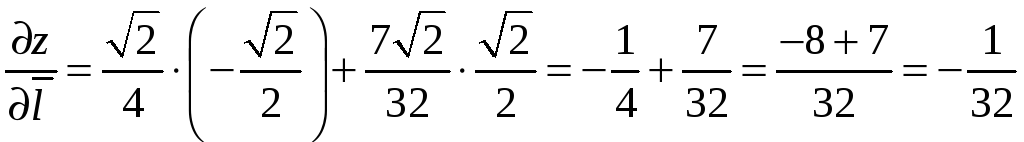Так как прозиводная по данному направлению отрицательна, то, следовательно, в точке М₀ по выбранному направлению функция убывает.