§6.2. Исследование функции на экстремум

Из определения (см. §6.1) следует, что понятие экстремума имеет локальный (местный) характер. Неравенство f(x) < f(x₀) (f(x) > f(x₀)) может, не выполняться для всех значений x, входящих в область определения функции, оно должно выполняться лишь в некоторой окрестности точки x₀. В области определения функция может иметь несколько локальных экстремумов.

Необходимое условие экстремума

 Если в некоторой точке x₀(a; b) функция y = f(x), непрерывная на интервале (a; b), имеет экстремум, то в самой точке x₀ производная данной функции равна нулю или не существует.

Возможны два случая: 1) в точке x₀ существует производная функции f(x), тогда по теореме Ферма f(x₀) = 0, 2) в точке x₀ производная функции не существует.

 Говорят, что в точке x₀(a; b) выполнено необходимое условие экстремума функции y = f(x), если в точке x₀ первая производная равна нулю, или не существует.

 Точки, в которых выполнено необходимое условие экстремума называют критическими точками первого рода или точками, подозрительными на экстремум. Те критические точки, в которых f(x) = 0, называют стационарными. В стационарных точках касательная, проведенная к графику функции, параллельна оси OX.

Замечание. Необходимое условие экстремума не является достаточным. Например, в точке x = 0 выполнено необходимое условие экстремума функции y = x³ (f(0) = 0). Однако, в точке x = 0, как и в остальных точках числовой оси, функция возрастает (и, следовательно, не имеет экстремума). С более сложными примерами мы познакомимся позднее.

Первое достаточное условие экстремума

 Пусть функция дифференцируема в некоторой -окрестности точки x₀ за исключением, быть может, самой точки x₀ (в самой точке x₀ она предполагается, как минимум – непрерывной). Если f(x) > 0 x(x₀ – ; x₀) и f(x) < 0 x(x₀; x₀ + ), то есть производная меняет знак с плюса на минус при переходе через точку x₀, то в точке x₀ функция имеет локальный максимум. Если производная меняет знак с минуса на плюс,– то минимум. Если же производная при переходе через точку x₀ знака не меняет, то в точке x₀ функция экстремума не имеет.

Рассмотрим случай, когда при переходе через точку x₀ производная меняет знак с плюса на минус. Выберем произвольно x(x₀ – ; x₀). Применим формулу Лагранжа (6.2) к функции f(x) на промежутке [x; x₀]:

. (6.3) Так как по условию f(x) > 0 x(x₀ – ; x₀), то f(с) > 0, кроме того, x₀ – x > 0. Из формулы (6.3) видно, что f(x₀) – f(x) > 0 или f(x₀) > f(x).

Выберем теперь произвольную точку x(x₀; x₀ + ) и применим формулу Лагранжа к функции f(x) на промежутке [x₀; x]:

. (6.4) По условию на интервале (x₀; x + δ) f(x) < 0 и, следовательно, f(с) < 0. Кроме того, x – x₀ > 0. Из формулы (6.4) следует, что f(x) – f(x₀) < 0 или, как и в предыдущем случае, f(x₀) > f(x). Таким образом, мы доказали, что в точке x₀ функция имеет локальный максимум.

Аналогично доказываются остальные утверждения теоремы.

Пример 6.1. Исследовать на экстремум функцию .

Решение. Найдем производную данной функции и определим критические точки первого рода.

.

Очевидно, что первая производная исходной функции обращается в ноль в точке x₀ = 1 и не существует в точке x₁ = 0. Однако из этих двух найденных точек, подозрительной на экстремум является только точка x₀ = 1. Точка x₁ = 0 не входит в область определения исходной функции и, следовательно, не является критической. Исследуем знак первой производной на всей области определения функции , т.е. при всех x > 0 (рис. 6.1):

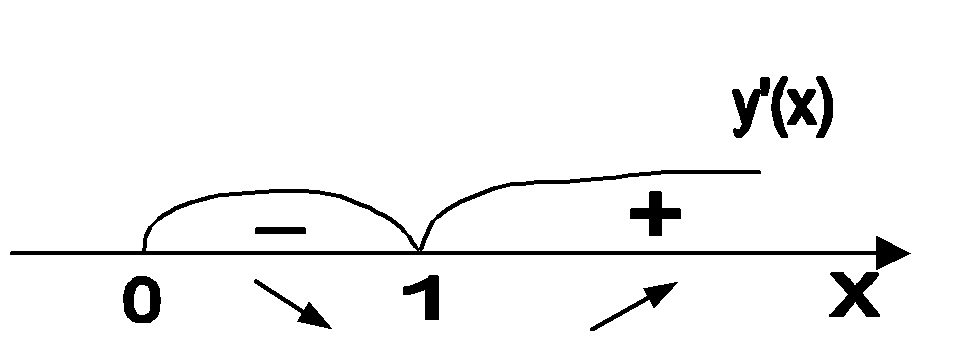
Рис. 6.1.

На промежутке x(0; 1) первая производная меньше нуля, следовательно функция убывает (обозначается y(x)). При x(1; +) производная больше нуля, следовательно, функция возрастает (обозначается y(x)). В точке x = 1 функция имеет минимум, причем y_min = y(1) = 1 – ln1 = 1.

Пример 6.2. Исследовать на экстремум функцию .

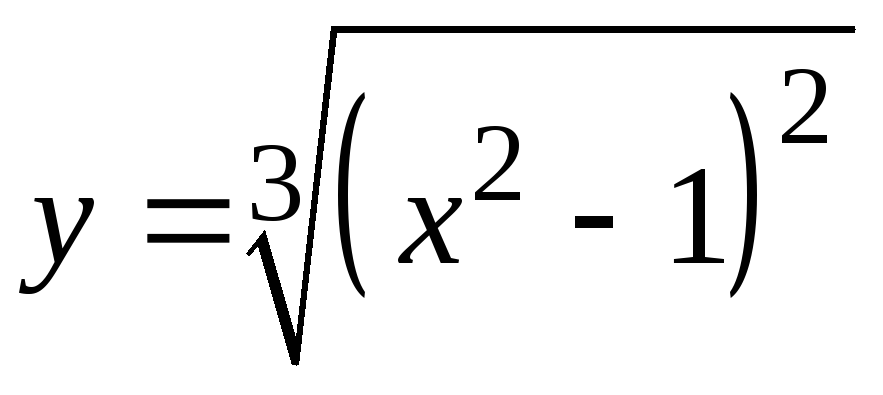Решение. Найдем производную данной функции и определим критические точки первого рода.

.

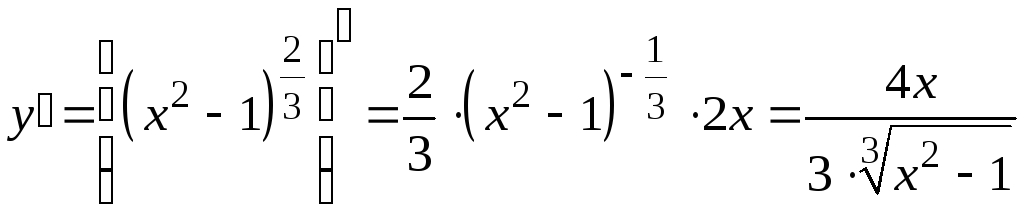Критическими точками первого рода данной функции являются точка x₁ = 0, в которой первая производная обращается в 0, и точки x₂ = 1 и x₃ = –1, в которых первая производная данной функции не существует. Заметим, что во всех найденных точках исходная функция определена и, следовательно, может иметь экстремум. Исследуем знак первой производной на всей области определения исходной функции 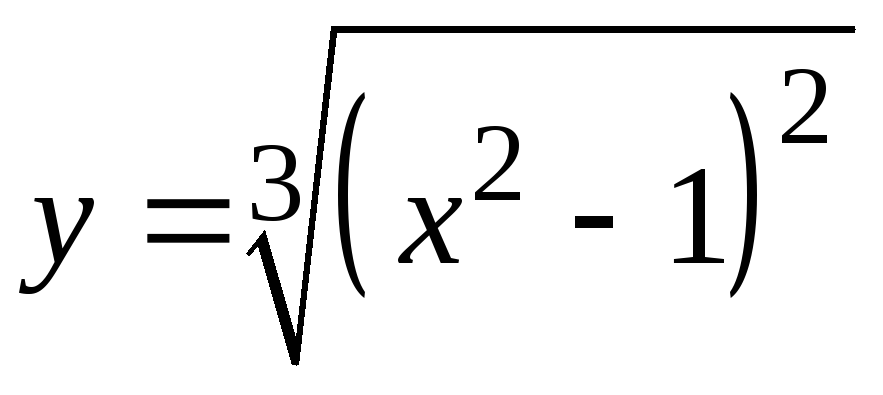, т.е. при всех действительных x (рис. 6.2):

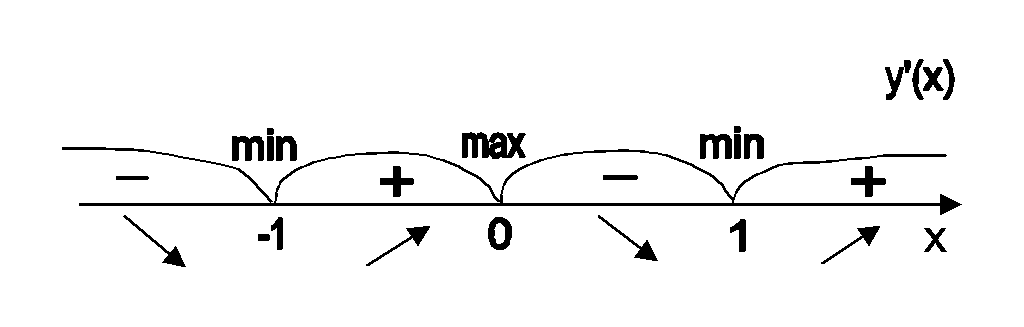
Рис. 6.2.

В точках первая производная меньше нуля, следовательно, функция убывает. В точках производная больше нуля, следовательно, функция возрастает. В точках x = 1 первая производная меняет знак с минуса на плюс, следовательно, функция в этих точках имеет минимум (y_min = y(1) = 0). В точке x = 0 первая производная меняет знак с плюса на минус, следовательно, функция имеет максимум (y_max = y(0) = 1).

Заметим, что в приведенном примере функция имеет минимумы в тех точках, в которых первая производная не существует, т.е. не является гладкой. График исходной функции в этих имеет изломы (рис. 6.6).