- •Часть II
- •Введение
- •Глава 6. Полное исследование функции и построение графика
- •§6.1. Экстремум функции. Монотонность
- •§6.2. Исследование функции на экстремум
- •Необходимое условие экстремума
- •Первое достаточное условие экстремума
- •§6.3. Направление выпуклости и точки перегиба графика функции
- •§6.4. Асимптоты графика функции
- •§6.5. Полное исследование функции и построение графика
- •Глава 7. Неопределенный интеграл
- •§7.1. Определение и свойства неопределенного интеграла
- •Свойства неопределенного интеграла
- •§7.2. Табличное интегрирование
- •§7.3. Подведение множителя под знак дифференциала
- •§7.4. Замена переменной под знаком неопределенного интеграла
- •§7.5. Метод интегрирования по частям
- •§7.6. Интегрирование выражений, содержащих квадратный трехчлен в знаменателе
- •§7.7. Интегрирование тригонометрических функций
- •Глава 8. Определенный интеграл.
- •§8.1. Задача о площади криволинейной трапеции. Определение определенного интеграла
- •§8.2. Свойства определенного интеграла. Формула Ньютона-Лейбница
- •§8.3. Замена переменной и интегрирование по частям под знаком определенного интеграла
- •§8.4. Приложения определенных интегралов
- •Вычисление площадей плоских фигур
- •Вычисление длины дуги плоской кривой
- •Вычисление объема тела с известным поперечным сечением.
- •Вычисление объема тела вращения
- •§8.5. Несобственные интегралы
- •Глава 9. Функции нескольких переменных
- •§9.1. Область определения функции нескольких переменных. Непрерывность
- •§9.2. Линии уровня функции двух переменных
- •§9.3. Частные производные первого порядка
- •§9.4. Градиент функции нескольких переменных. Производная по направлению
- •§9.5. Дифференциал функции нескольких переменных и его применение к приближенным вычислениям
- •§9.6. Частные производные высших порядков
- •§9.7. Экстремум функции двух переменных
- •Глава 10. Дифференциальные уравнения
- •§10.1. Дифференциальные уравнения первого порядка
- •1. Дифференциальные уравнения с разделяющимися переменными
- •2. Однородные дифференциальные уравнения 1-го порядка
- •3. Линейные дифференциальные уравнения 1-го порядка
- •§10.2. Простейшие случаи понижения порядка дифференциального уравнения
- •1. Дифференциальные уравнения вида .
- •2. Дифференциальные уравнения вида .
- •3. Дифференциальные уравнения вида .
- •§10.3. Линейные дифференциальные уравненния второго порядка с постоянными коэффициентами
- •Литература
§6.4. Асимптоты графика функции
Асимптотой графика функции y = f(x) называется прямая линия, к которой неограниченно приближаются точки графика функции при их неограниченном удалении от начала координат. При этом график функции может пересекать асимптоту не более чем конечное число раз.
Различают вертикальные, горизонтальные и наклонные асимптоты.
Прямая линия x = x0
является вертикальной асимптотой
графика функции y =
f(x)
слева (справа), если соответствующий
односторонний предел в точке x0
(ч. 1, гл. 4) равен бесконечности
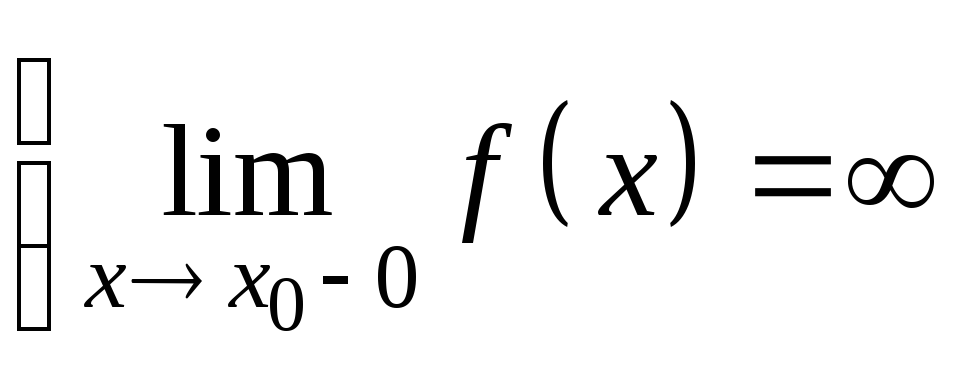 или
или
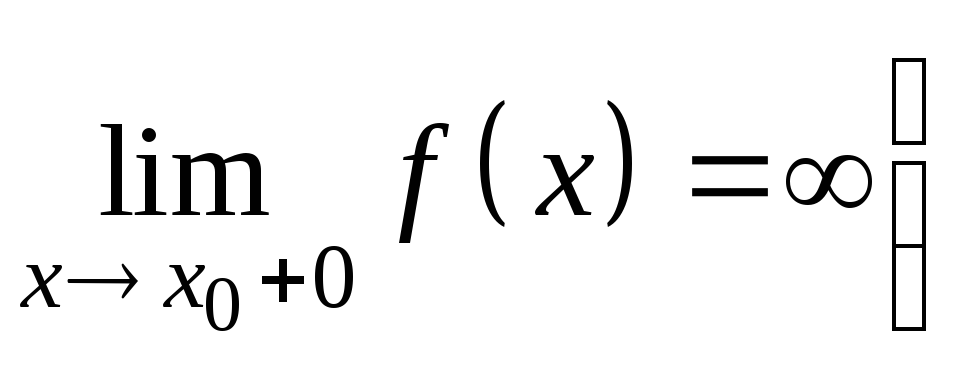 .
.
Если прямая линия x = x0 является вертикальной асимптотой графика функции y = f(x), то, очевидно, что x0 является точкой разрыва второго рода данной функции.
Прямая линия y = y0
является горизонтальной асимптотой
графика функции y =
f(x)
при
![]() (
(![]() ),
если
),
если
![]() (
(![]() ).
).
Если существуют и конечны пределы
 и
и
![]() ,
(6.5)
,
(6.5)
то прямая линия y =
k1x
+ b1 является
наклонной асимптотой графика функции
y = f(x)
при
![]() .
.
Если существуют и конечны пределы
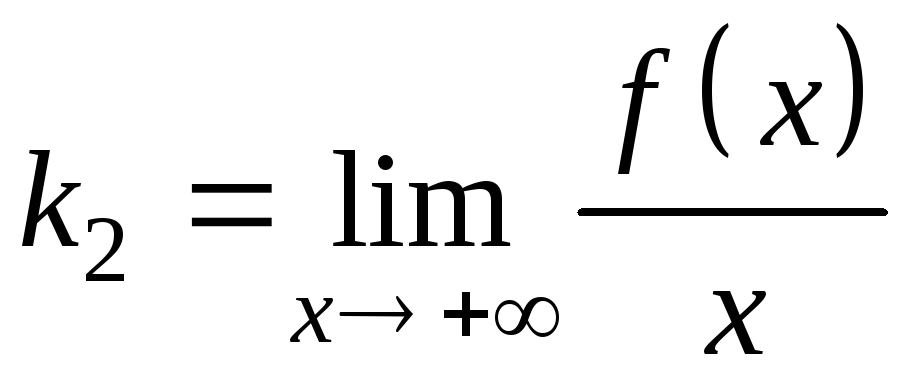 и
и
![]() ,
(6.6)
,
(6.6)
то прямая линия y =
k2x
+ b2 является
наклонной асимптотой графика функции
y = f(x)
при
![]() .
.
Очевидно, что горизонтальные асимптоты являются частным случаем наклонных (при k = 0).
Пример 6.4. Найти асимптоты графика
функции
![]() .
.
Решение. 1) Найдем односторонние
пределы в точке разрыва данной функции:
![]() ,
,
![]() .
Так как оба предела равны бесконечности,
то прямая линия x = 3
является вертикальной асимптотой
графика функции (как слева, так и справа).
.
Так как оба предела равны бесконечности,
то прямая линия x = 3
является вертикальной асимптотой
графика функции (как слева, так и справа).
-
Очевидно, что
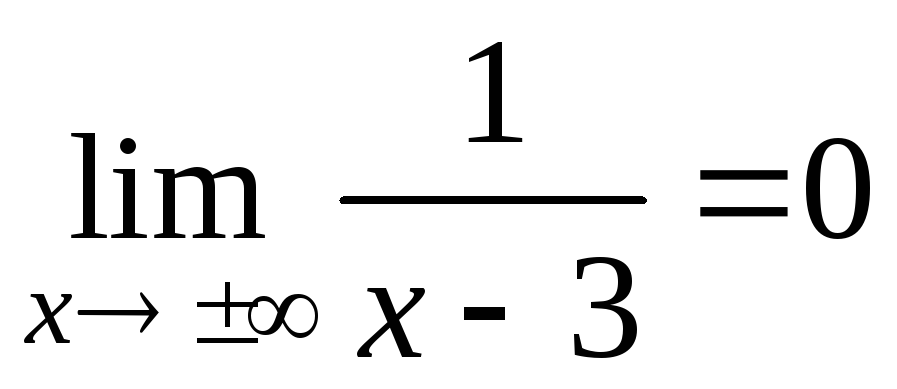 ,
следовательно, прямая линия y
= 0 (ось OX) является
горизонтальной асимптотой. График
данной функции схематически изображен
на рис. 6.7.
,
следовательно, прямая линия y
= 0 (ось OX) является
горизонтальной асимптотой. График
данной функции схематически изображен
на рис. 6.7.
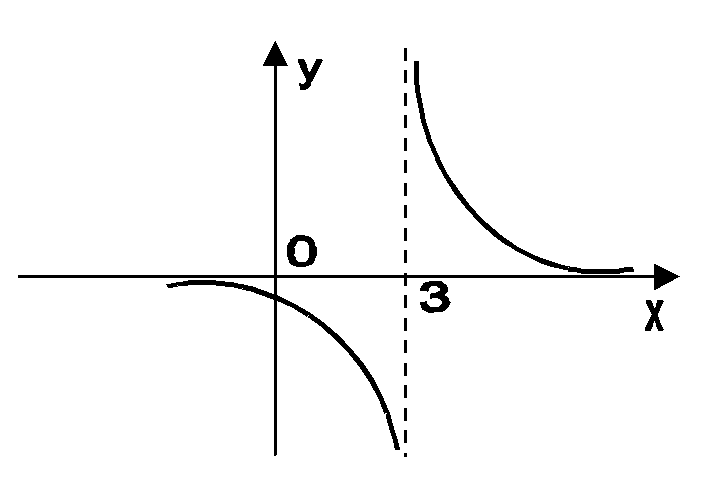
Рис. 6.7.
Пример 6.5. Найти асимптоты графика
функции
![]() .
.
Решение. 1) Найдем односторонние пределы в точке разрыва данной функции (в точке x = 0).
Если
![]() ,
то
,
то
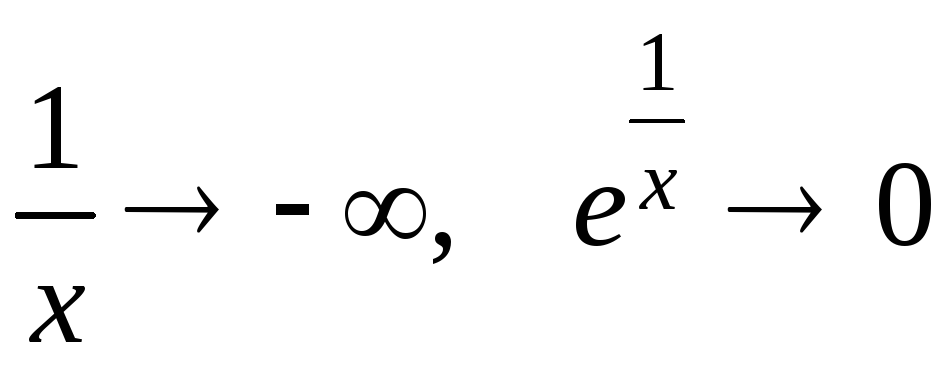 и, следовательно,
и, следовательно,
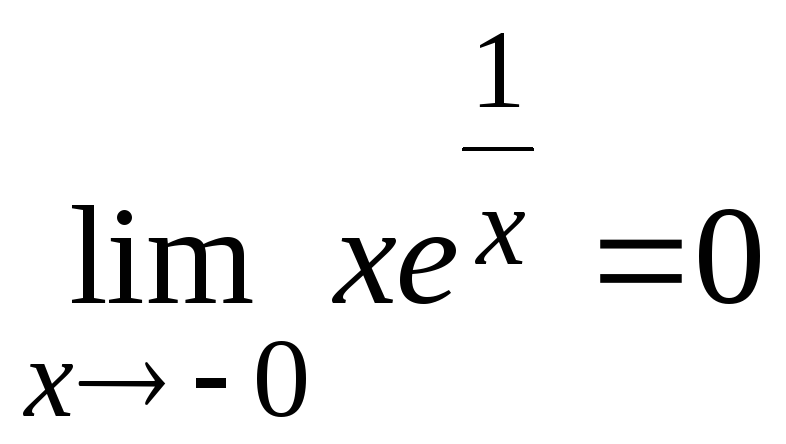 .
.
Если
![]() ,
то
,
то
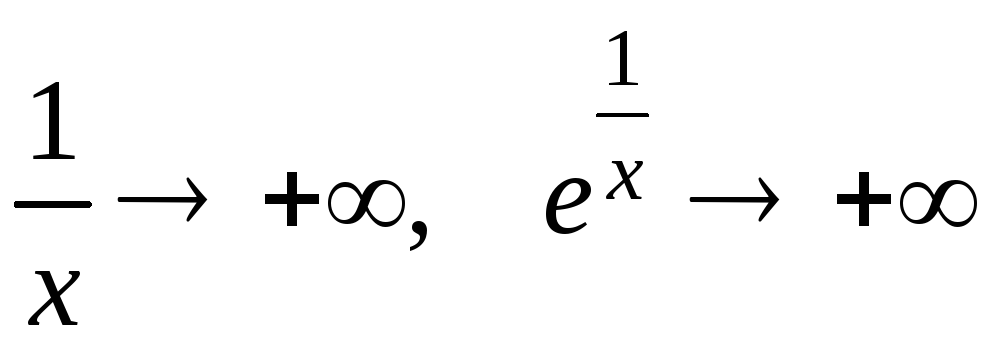 .
В этом случае предел вычисляем по
правилу Лопиталя:
.
В этом случае предел вычисляем по
правилу Лопиталя:
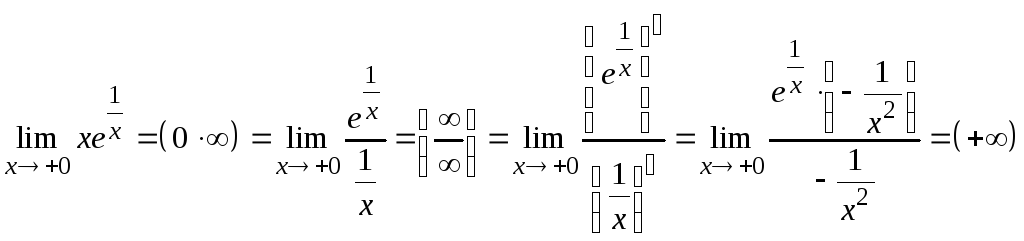 .
.
Следовательно, прямая линия y = 0 является вертикальной асимптотой графика исходной функции справа.
2) Наклонные асимптоты будем искать, используя формулы (6.5) – (6.6).
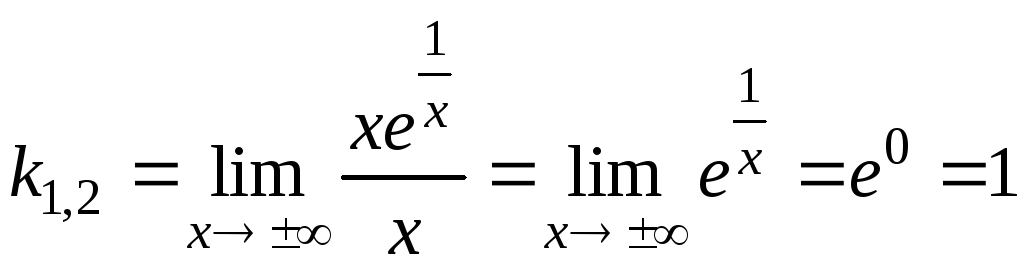 ,
,
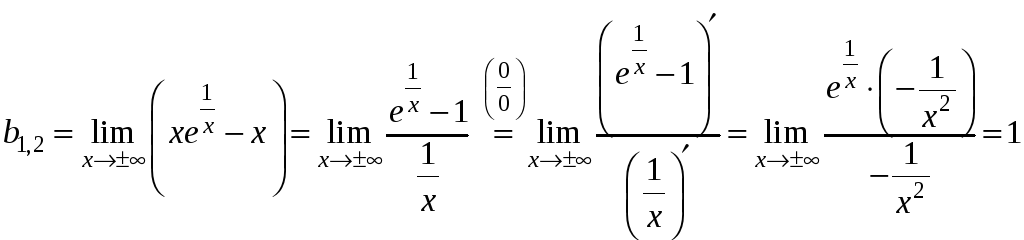 .
.
Следовательно, прямая линия y
= x + 1 является наклонной
асимптотой графика исходной функции
(при
![]() и при
и при
![]() ).
График функции
).
График функции
![]() постройте самостоятельно (в качестве
упражнения).
постройте самостоятельно (в качестве
упражнения).
§6.5. Полное исследование функции и построение графика
Схема общего исследования функции:
-
Найти область определения функции
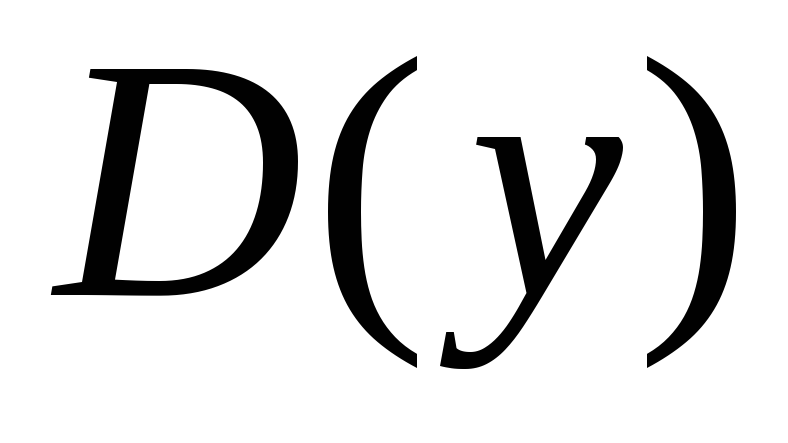 .
. -
Найти область значений функции
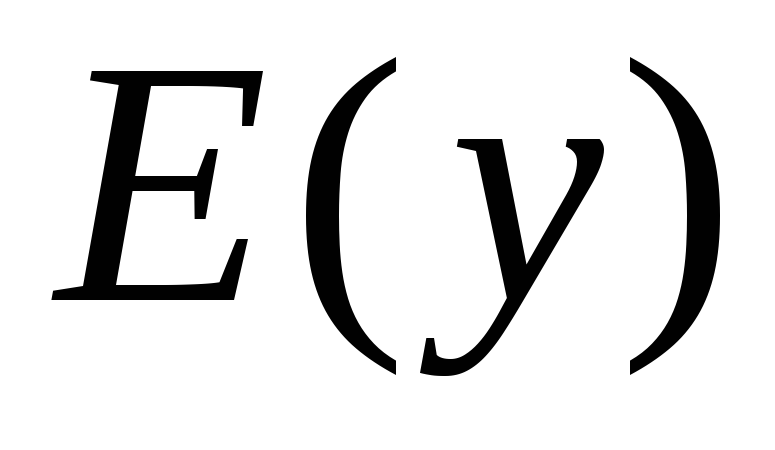 (если это возможно), точки пересечения
графика функции с осями координат,
участки знакопостоянства.
(если это возможно), точки пересечения
графика функции с осями координат,
участки знакопостоянства. -
Определить вид функции (четная, нечетная, общего вида).
-
Определить периодичность функции.
-
Исследовать функцию на непрерывность. Найти вертикальные, наклонные или горизонтальные асимптоты графика функции.
-
Найти критические точки первого рода.
-
Найти критические точки второго рода.
-
Заполнить таблицу исследования.
-
По результатам исследования построить график функции.
Пример 6.6. Провести полное исследование
и построить график функции
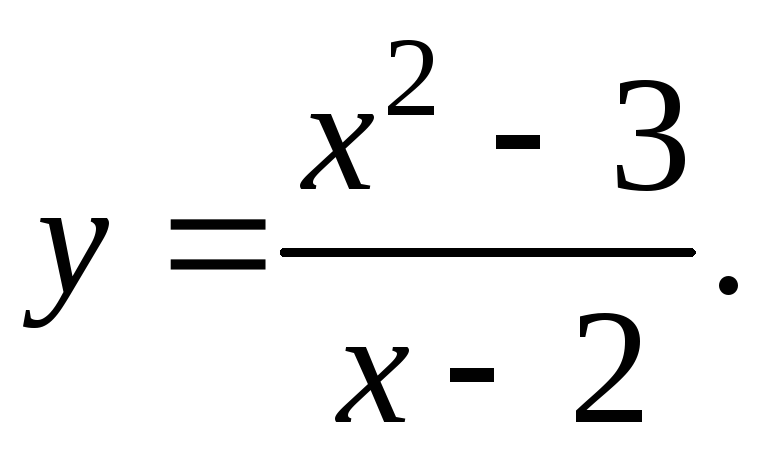
Решение.
-
Область определения
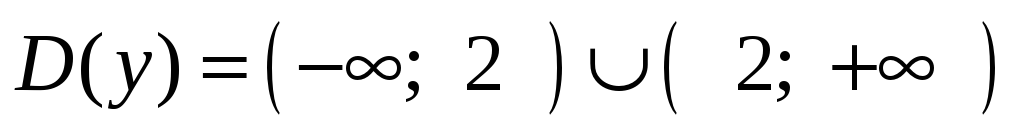 .
. -
Пусть x = 0, тогда y = 1,5. Пусть y = 0, тогда x =
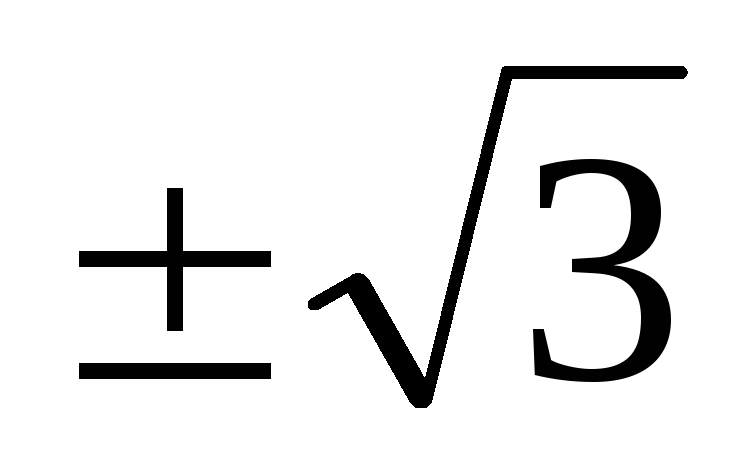 .
То есть точки (0; 3/2) и (
.
То есть точки (0; 3/2) и (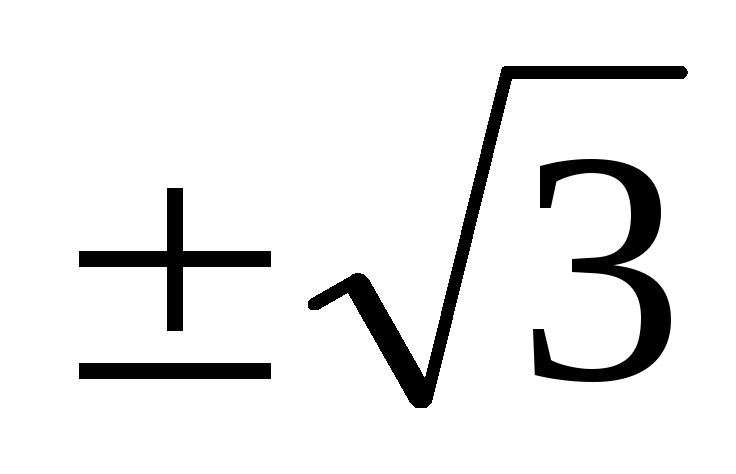 ;
0) – являются точками пересечения
графика функции с осями координат.
Если
;
0) – являются точками пересечения
графика функции с осями координат.
Если
 ,
то y(x)
< 0. Если
,
то y(x)
< 0. Если
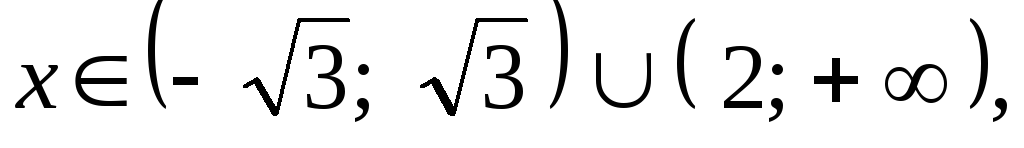 то y(x)
> 0.
то y(x)
> 0. -
Функция общего вида, т. е. не является ни четной, ни нечетной. Действительно,
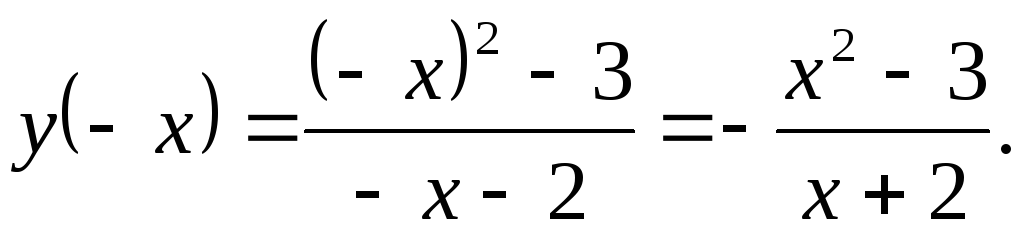 То есть y(-x)
y(x)
и y(-x)
- y(x).
То есть y(-x)
y(x)
и y(-x)
- y(x). -
Функция не является периодической, так как она имеет только одну точку разрыва.
-
Функция непрерывна в области определения, так как является дробно-рациональной. Для исследования типа разрыва в точке x = 2, найдем односторонние пределы
![]()
Следовательно, точка x = 2 является точкой разрыва второго рода, и прямая линия x = 2 является вертикальной асимптотой графика функции.
Уравнения наклонных (горизонтальных) асимптот графика функции будем искать в виде: y=kx+b, где k и b определяются по формулам (6.5) – (6.6):
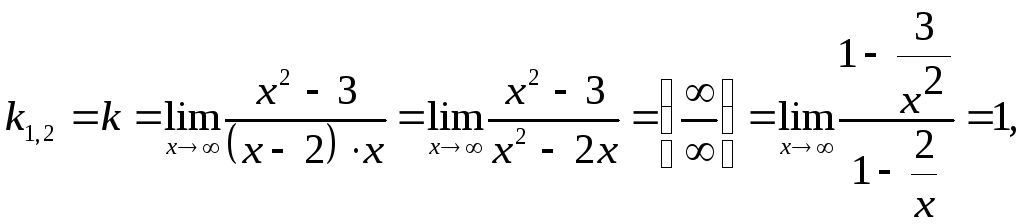
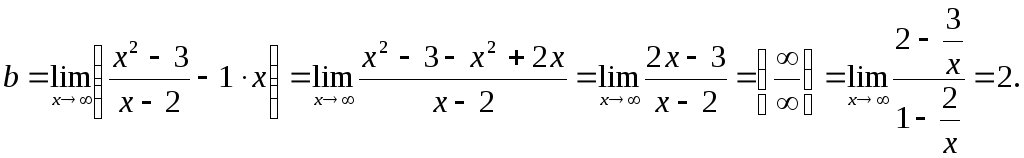
Таким образом, прямая y = x + 2 является наклонной асимптотой.
-
Найдем первую производную функции:
![]()
![]()
Итак, критическими точками 1-го рода являются точки x = 1 и x = 3. Точка x=2 критической не является, т. к. она не принадлежит области определения функции.
-
Найдем вторую производную функции:
![]()
![]()
Критических точек второго рода функция не имеет.
-
Составим таблицу исследования функции:
|
x |
(–; 1) |
1 |
[1; 2) |
2 |
(2; 3) |
3 |
(3; ) |
|
y(x) |
+ |
0 |
– |
Не сущ. |
– |
0 |
+ |
|
y(x) |
– |
– |
– |
Не сущ. |
+ |
+ |
+ |
|
y(x) |
|
max y = 2. |
|
Не сущ. |
|
min y= 6. |
|
-
Построим график функции (рис.6.8):
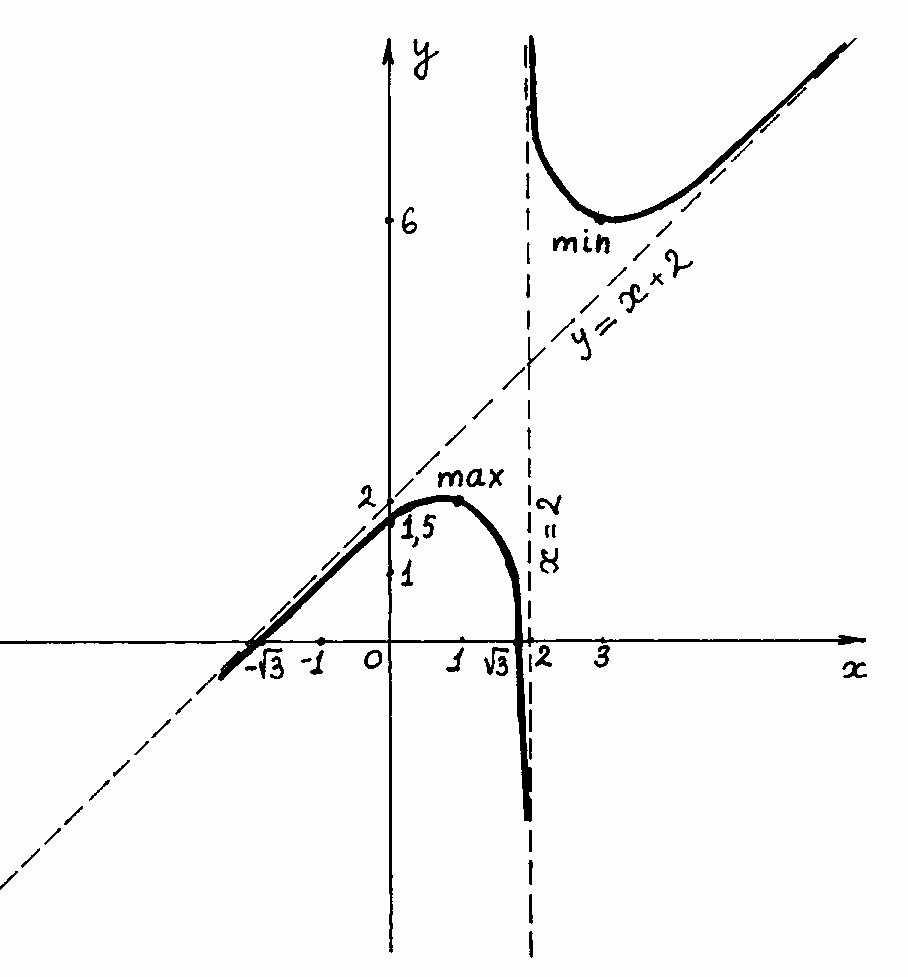
Рис. 6.8.