§10.3. Линейные дифференциальные уравненния второго порядка с постоянными коэффициентами

 Линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами дазываются дифференциальные уравнения вида

. (10.9)

В данном пособии мы ограничимся рассмотрением только линейных однородных дифференцыальных уравнений второго порядка с постоянными коэффициентами, т.е. уравнений вида

. (10.10)

 Характеристическим уравнением дифференциального уравнения (10.10) называется квадратное уравнеие

, (10.11)

которое получается из уравнения (10.10) путем заиены n – ой производной функции на соответствующую степень k.

 Если уравнение (10.11) имеет два различных действительных корня , то общим решением дифференциального уравнения (10.10) является

.

 Если уравнение (10.11) имеет два равных действительных корня , то общим решением дифференциального уравнения (10.10) является

.

 Если уравнение (10.11) не имеет действительных корней, а имеет два комплексно-сопряженных корня (где i² = – 1), то общим решением дифференциального уравнения (10.10) является

.

Пример 10.8. Найти общее решение дифференциального уравнения:

.

Решение. Найдем корни характеристического уравнения .

.

Следовательно, общим решением дифференциального уравнения является:

.

Пример 10.9. Решить задачу Коши

.

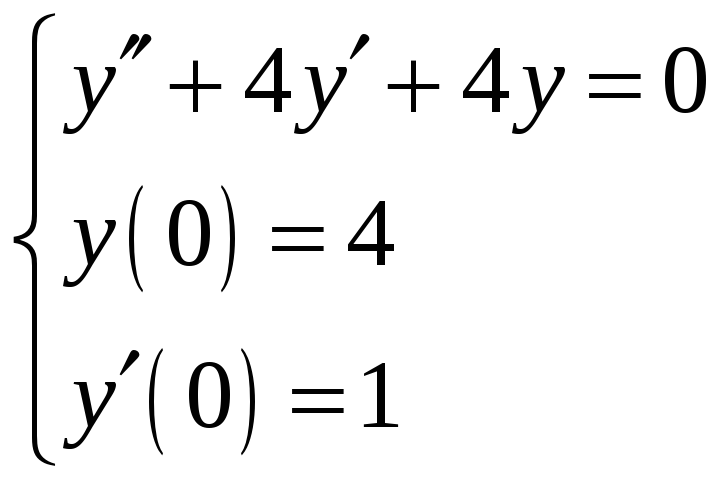Решение. Найдем корни характеристического уравнения .

.

Следовательно, общим решением дифференциального уравнения является .

Найдем производную и подставим в и начальные условия:

.

Решая данную систему, мы найдем значения констант , при которых решение дифференциального уравнения удовлетворяет начальным условиям.

Таким образом, мы нашли решение исходной задачи Коши:

.

Пример 10.10. Найти общее решение дифференциального уравнения

.

Решение. Найдем корни характеристического уравнения .

.

Следовательно, общим решением дифференциального уравнения является:

.

Литература

1. Демидович Б.П. Краткий курс высшей математики / Б.П. Демидович, В.А. Кудрявцев. – М.: Астель. АСТ, 2001. – 655 с.

2. Минорский В.П. Сборник задач по высшей математике: Учеб. пособие для втузов / В.П. Минорский. – 14-е изд. – М.: Изд-во физ.-мат. лит., 2001. – 366 с.

3. Шипачев В.С. Основы высшей математики: Учеб. пособие для втузов / В.С. Шипачев; Под ред. акад. А.Н. Тихонова. – 2-е изд. стереотипное– М.: Высш. шк., 1994.– 352 с.

4. Шипачев В.С. Сборник задач по высшей математике: Учеб. пособие / В.С. Шипачев. – М.: Высш. шк., 1994.– 192 с.

5. Шипачев В.С. Высшая математика: Учебник для студ. втузов / В.С. Шипачев. – 5-е изд., стереотипное – М.: Высш. шк., 2000.– 479 с.

6. Письменный Д.Т. Конспект лекций по высшей математике: Тридцать шесть лекций / Д.Т. Письменный. – М: Айрис-пресс, 2000,– Ч. 1.– 279 с.

7. Гусак А.А. Высшая математика: Учеб. для студ. втузов: В 2 т. / А.А. Гусак. – 3-е изд., стереотипное – Минск: Тетра Системс, 2001. – Т. 2.– 447 с.

Составители: доц. Фетисов Юрий Михайлович,

ст. преп. Уксусов Сергей Николаевич.

Редактор: Бунина Т.Д.