Глава 10. Дифференциальные уравнения

 Дифференциальным уравнением называется уравнение вида

, (10.1)

где x – независимая переменная, y(x) – неизвестная функция y⁽ⁱ⁾(x) – производная функции y(x) i-го порядка. Порядок старшей производной, входящей в уравнение (10.1), называется порядком дифференциального уравнения.

 Функция y(x), обращающая дифференциальное уравнение (10.1) в тождество, называется решением дифференциального уравнения. Как правило, дифференциальное уравнение имеет бесчисленное множество решений. Множество всех решений уравнения (10.1) называют общим решением дифференциального уравнения. Конкретный представитель общего решения (обычно удовлетворяющий какому-нибудь дополнительному требованию) называют частным решением дифференциального уравнения. Общее или частное решение дифференциального уравнения, полученное в виде неявной функции, называют соответственно общим или частным интегралом дифференциального уравнения.

С простейшими дифференциальными уравнениями вида мы сталкивались, решая задачу интегрирования функции.

Пример 10.1. Найти общее решение дифференциального уравнения: .

Решение. Очевидно, что – общее решение дифференциального уравнения, некоторые частные решения.

§10.1. Дифференциальные уравнения первого порядка

В общем случае дифференциальное уравнение первого порядка имеет вид:

(10.2)

 Задача нахождения частного решения дифференциального уравнения (10.2), удовлетворяющего некоторому начальному условию, называют задачей Коши:

(10.3)

Рассмотрим некоторые типы дифференциальных уравнений первого порядка.

1. Дифференциальные уравнения с разделяющимися переменными

 Дифференциальными уравнениями с разделяющимися переменными называются уравнения вида

. (10.4)

Общее решение дифференциальных уравнений с разделяющимися переменными находят с помощью метода, который так и называется «метод разделения переменных»:

1. В уравнении (10.4) производную представим, как частное дифференциалов .

2. Умножим обе части полученного уравнения на dx и разделим на g(y) 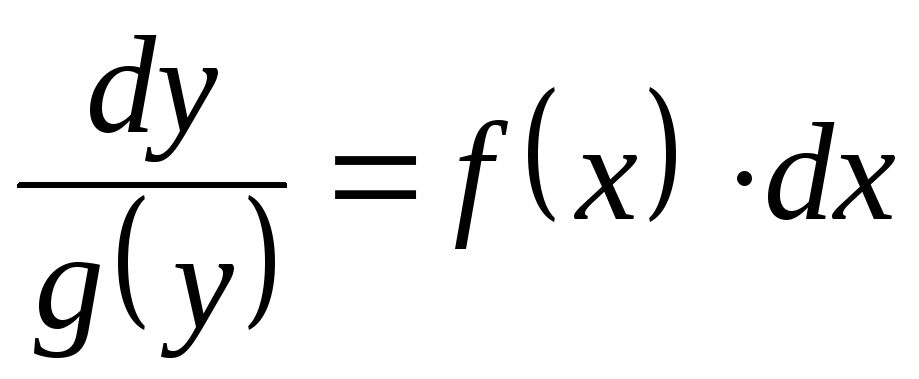(переменные разделились).

3. Интегрируя обе части полученного уравнения, находим общее решение исходного дифференциального уравнения .

Пример 10.2. Найти общее решение дифференциального уравнения: .

Решение. Очевидно, что данное уравнение является уравнением с разделяющимися переменными. Разделяя переменные, получим:

.

Таким образом, мы находим общий интеграл дифференциального уравнения: , или .

2. Однородные дифференциальные уравнения 1-го порядка

 Дифференциальные уравнения первого порядка называются однородными, если является однородной функцией. Т.е. , для любого .

Если – однородное дифференциальное уравнение первого порядка, то оно с помощью замены сводится к дифференциальному уравнению с разделяющимися переменными. При этом .

Пример 10.3. Решить задачу Коши:

Решение. Преобразуем данное дифференциальное уравнение к виду . Для этого разделим обе его части на dx:

, или . Подставляя x вместо x и y вместо y в правую часть полученного уравнения, мы убеждаемся в том, что оно является однородным:

.

Произведем замену переменной , . При этом наше дифференциальное уравнение примет вид:

. Откуда , или . Полученное дифференциальное уравнение является уравнением с разделяющимися переменными. Найдем его общее решение:

.

Откуда . Производя обратную замену , мы получим общий интеграл исходного дифференциального уравнения: , или . Найдем такое значение константы С, при котором общее решение дифференциального уравнения удовлетворяет начальному условию . Для этого подставим в общее решение: . Откуда .

Подставляя найденную константу С в общее решение мы получим искомое решение исходной задачи Коши:

.