§8.5. Несобственные интегралы

 Несобственными интегралами первого рода называются интегралы вида 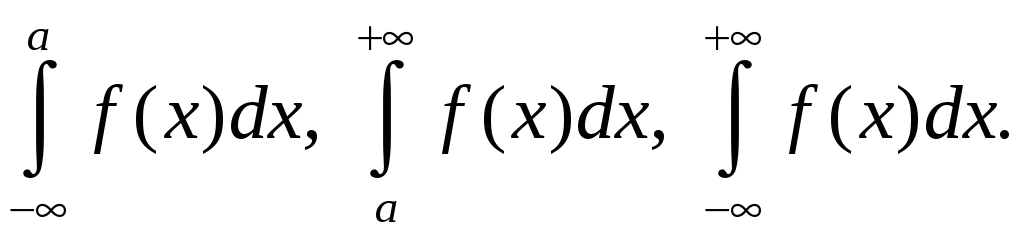Подынтегральная функция предполагается непрерывной на всем участке интегрирования.

 Если существует и конечен преде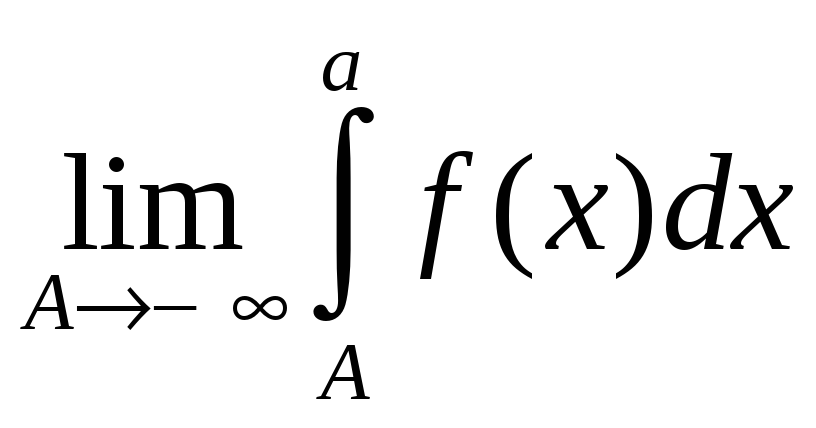л , то говорят, что несобственный интеграл 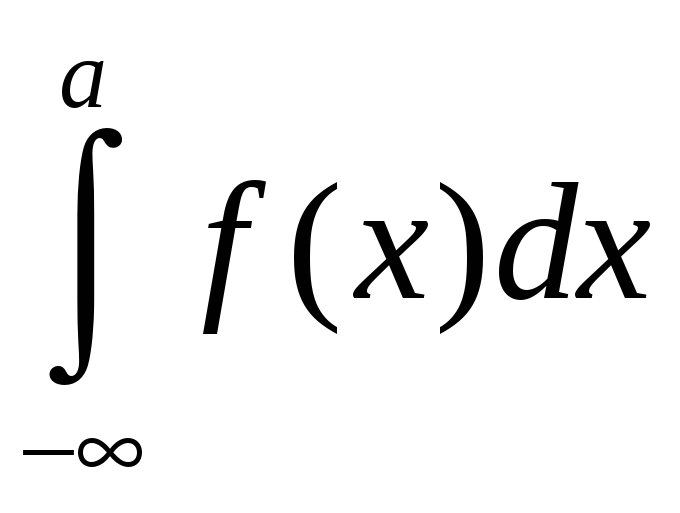сходится и равен

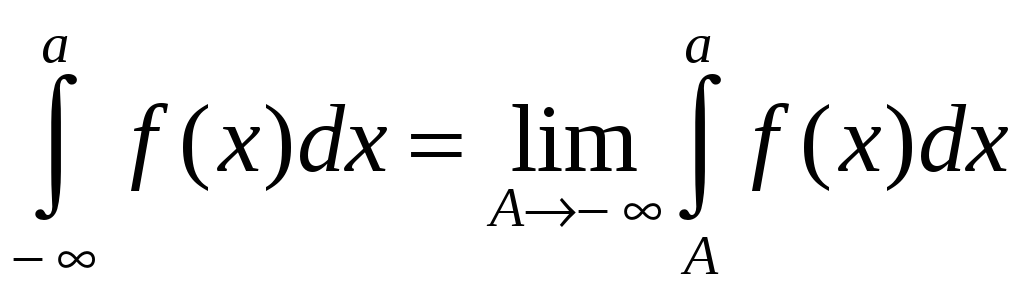. (8.19)

Аналогично определяются интегралы 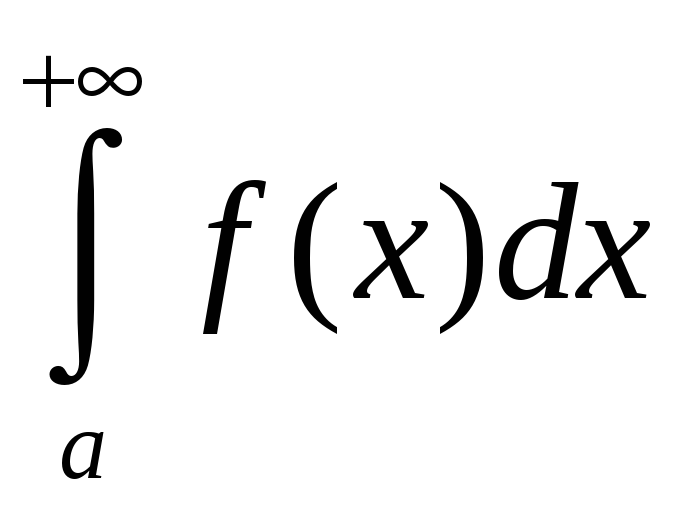и :

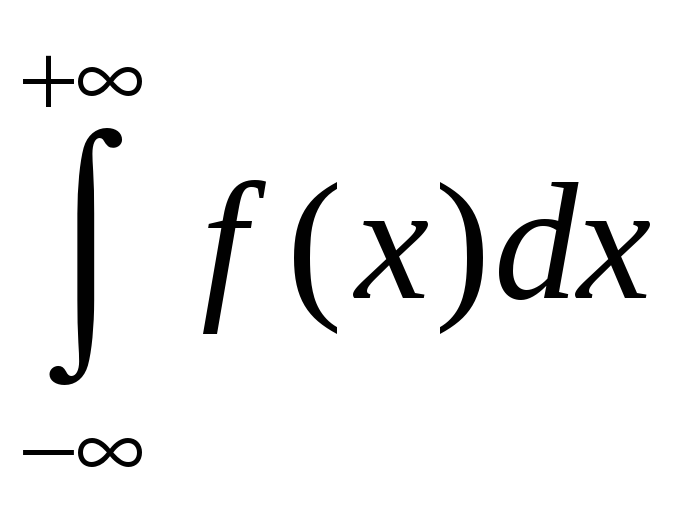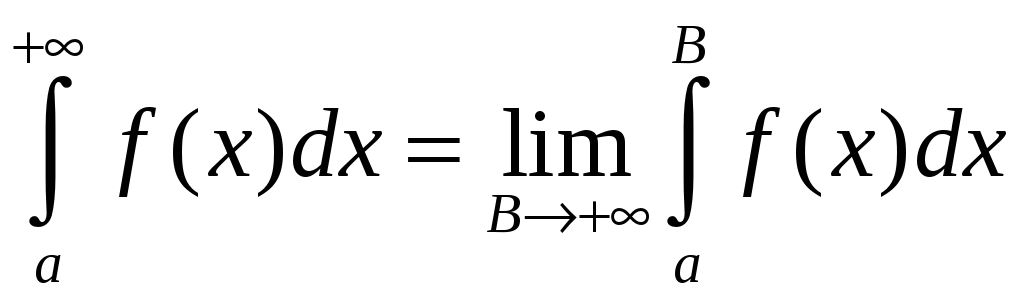, (8.20)

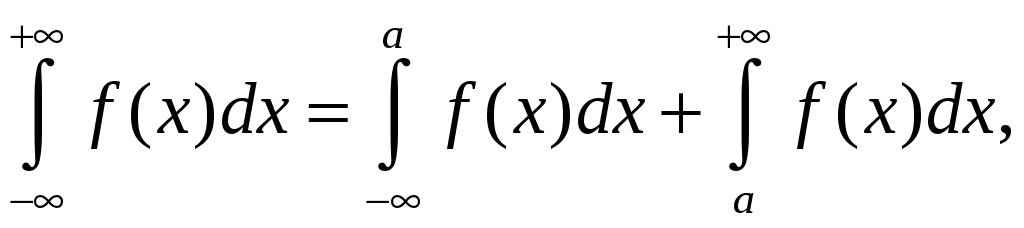(8.21) где а – любое действительное число. Причем про последний интеграл говорят, что он сходится тогда и только тогда, когда сходятся оба составляющих его интеграла.

Пример 8.10. Вычислить несобственный интеграл .

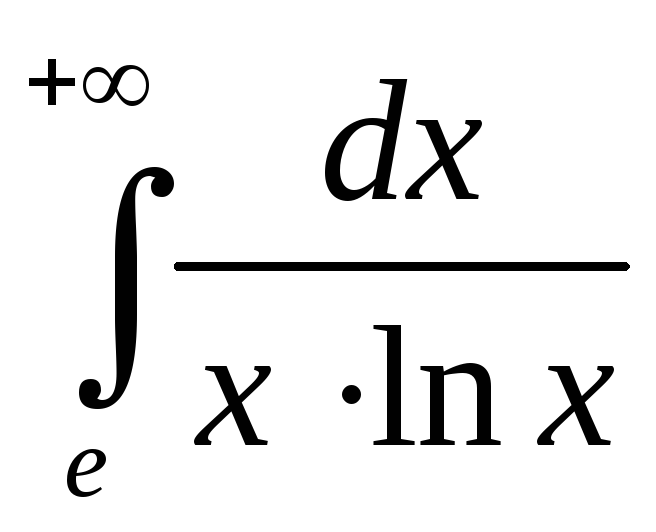Решение.

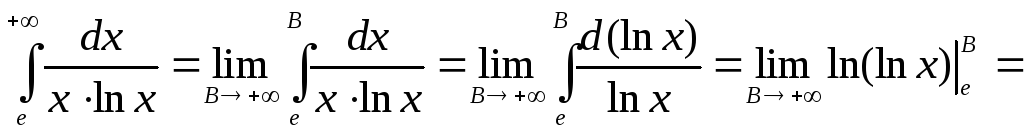
следовательно, интеграл – расходится.

Пример 8.11. Вычислить несобственный интеграл .

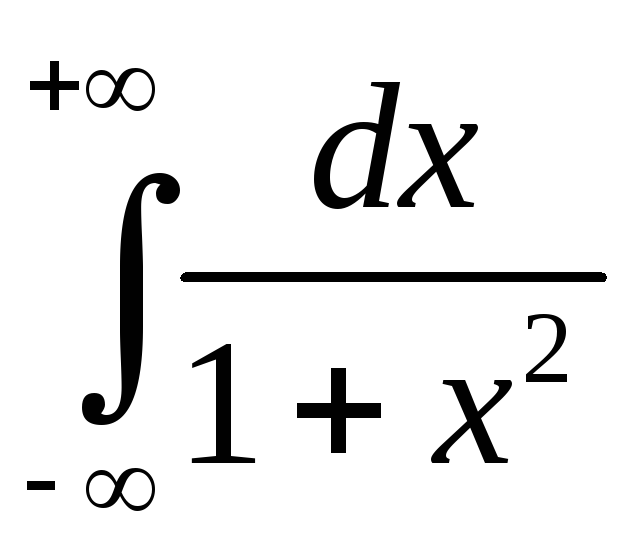Решение.

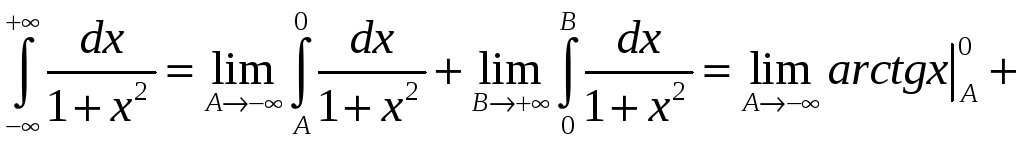
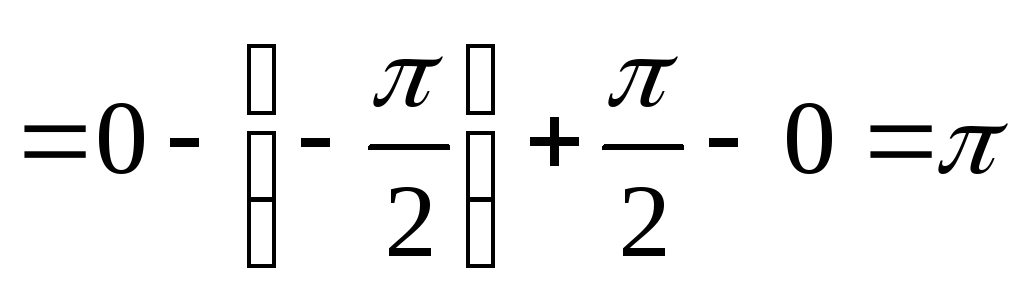. Данный интеграл – сходится.

 Несобственными интегралами второго рода называются интегралы вида: 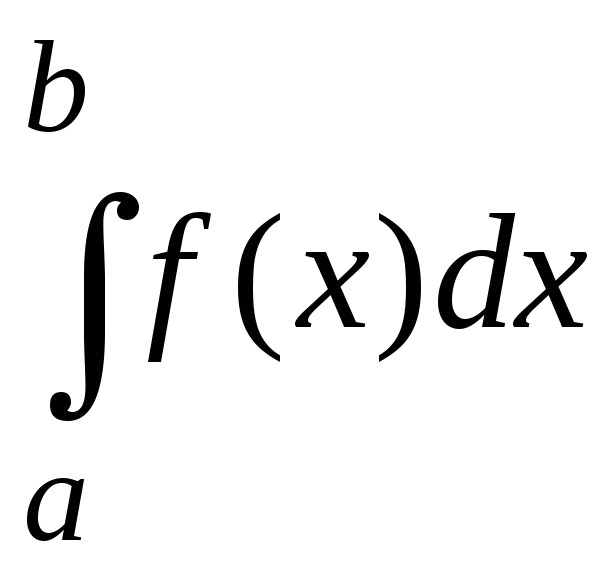, где подынтегральная функция f(x) имеет разрывы второго рода на промежутке [a; b]. Определяются несобственные интегралы второго рода по-разному, в зависимости от расположения точек разрыва на промежутке [a; b].

1. Предположим, что функция f(x) имеет единственную точку разрыва второго рода, лежащую внутри области интегрирования (c(a; b)).

Если существуют и конечны пределы и 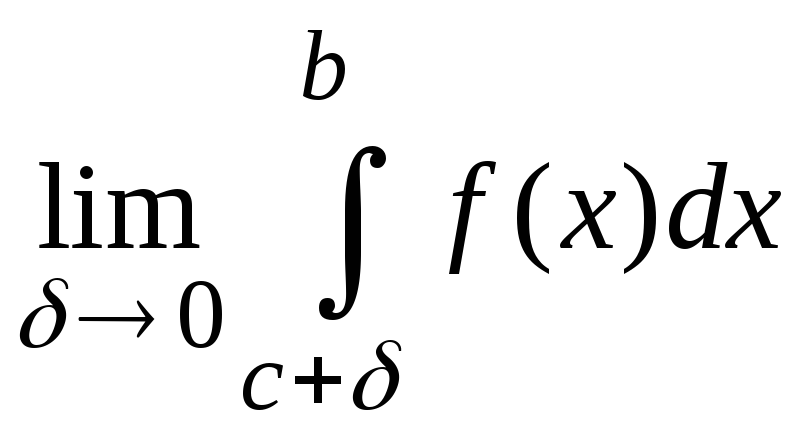, то говорят, что интеграл сходится и равен

. (8.22)

2. Пусть единственная точка разрыва функции f(x) совпадает с точкой а. Тогда, если существует и конечен преде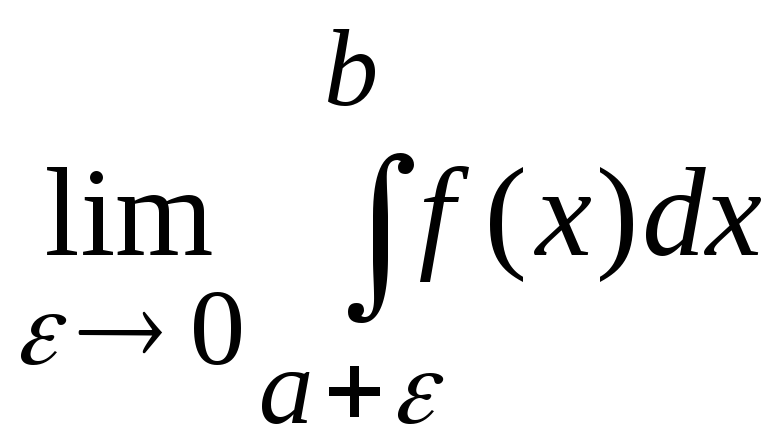л , то говорят, что интеграл 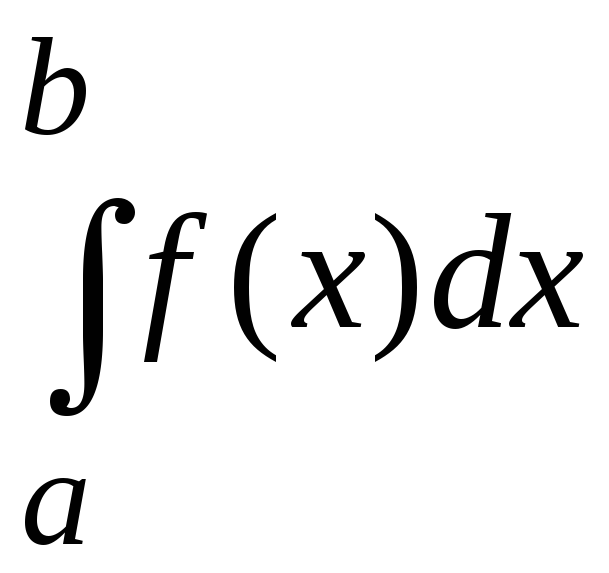– сходится, и равен

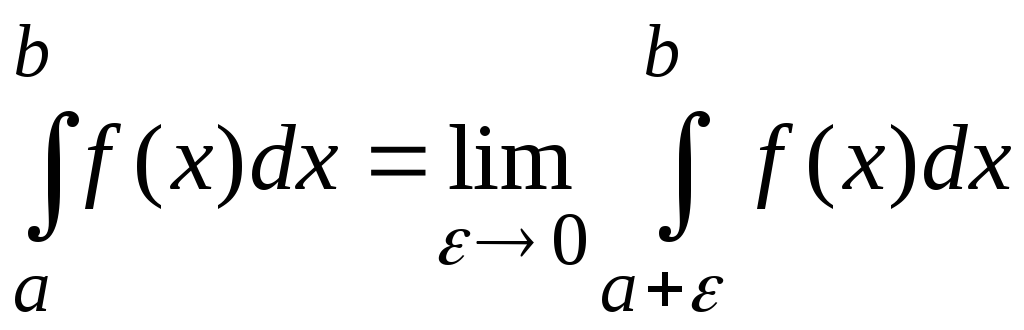. (8.23)

3. Пусть единственная точка разрыва функции f(x) совпадает с точкой b. Тогда, если существует и конечен преде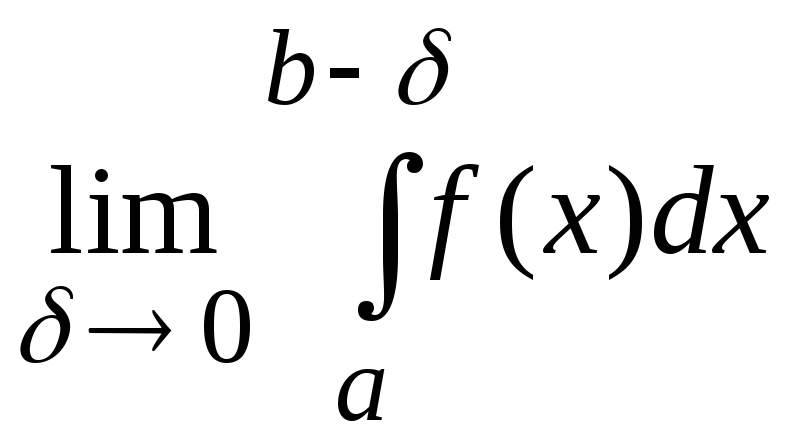л , то говорят, что интеграл 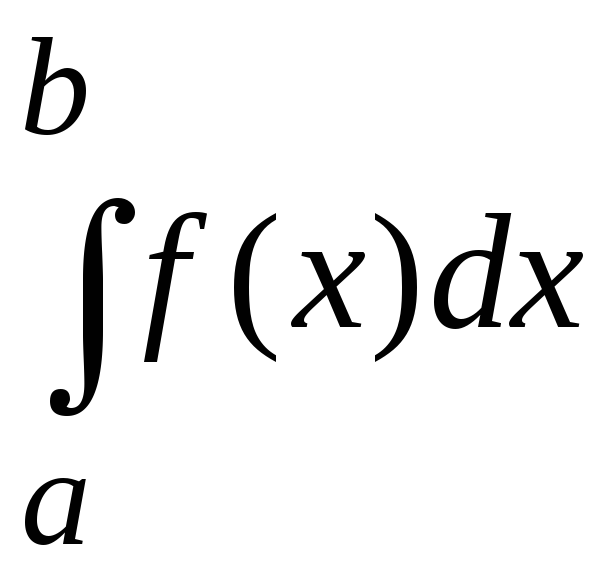сходится, и равен

. (8.24)

Всюду предполагается, что    и   .

Пример 8.12. Вычислить несобственный интеграл .

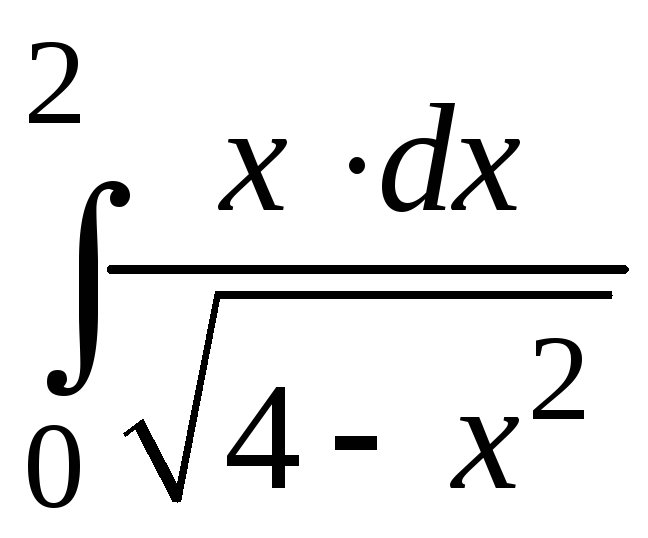Решение. Подынтегральная функция имеет разрыв второго рода в точке x = 2. Следовательно,

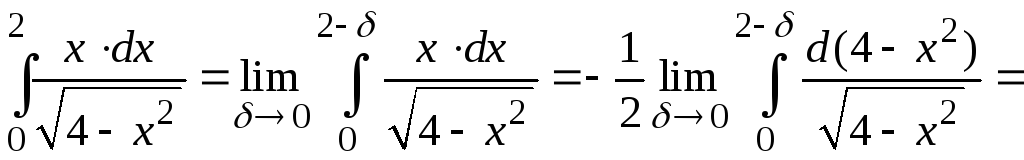
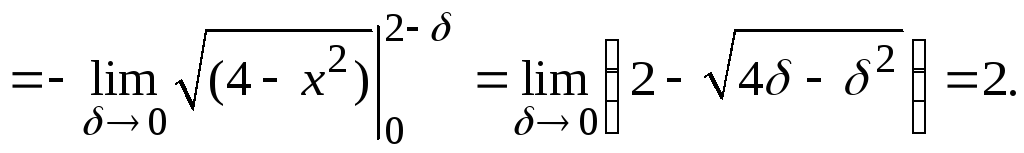
Пример 8.13. Вычислить несобственный интеграл .

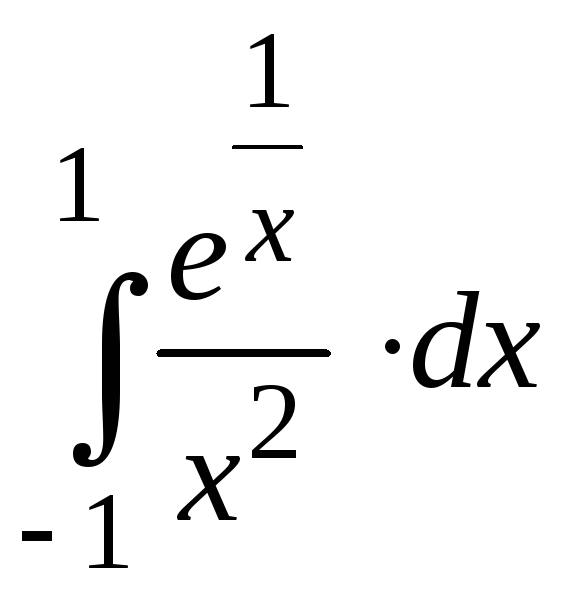Решение. Подынтегральная функция имеет разрыв второго рода в точке x = 0 (внутри области интегрирования). Следовательно,

.

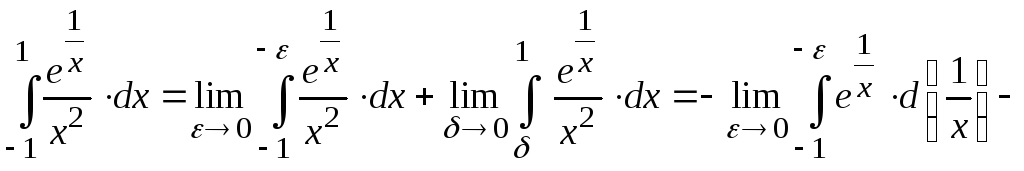
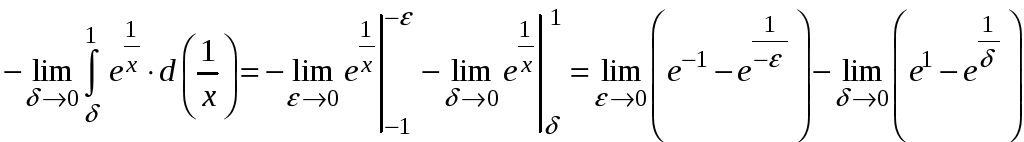Первый предел существует и конечен, но второй предел равен бесконечности ( при ). Следовательно, данный интеграл – расходится.

Глава 9. Функции нескольких переменных

§9.1. Область определения функции нескольких переменных. Непрерывность

 Функцией n переменных называется такое правило (закон) по которому каждому набору, состоящему из n переменных , взятому из некоторой области D n-мерного пространства , ставится в соответствие единственное число z. В частном случае

 Функцией 2-х переменных называется такое правило (закон) по которому каждой точке M(x; y), принадлежащей некоторой области D, плоскости xOy ставится в соответствие единственное число z.

Множество точек в пространстве с координатами образуют некоторую поверхность (рис. 9.1), возвышающуюся над областью D (геометрический смысл функции двух переменных).

 О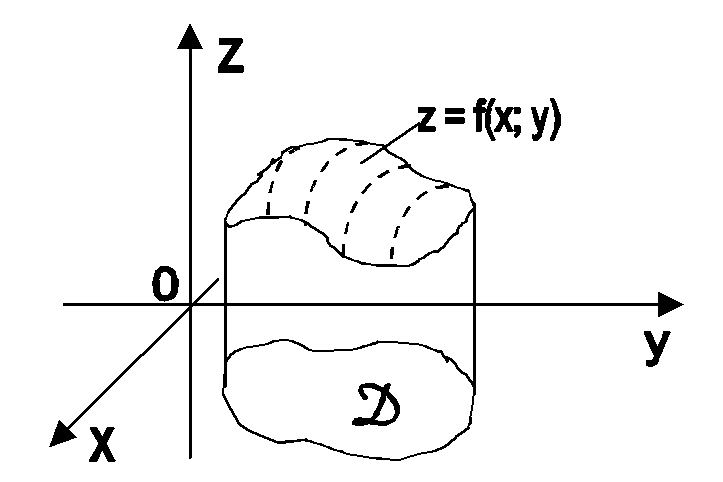бласть D, для которой построено указанное выше соответствие, называется областью опреде-

Рис. 9.1 ления функции .

Пример 9.1. Найти область определения функции

Решение. Искомая область определения является множеством точек на плоскости xOy, удовлетворяющих системе неравенств 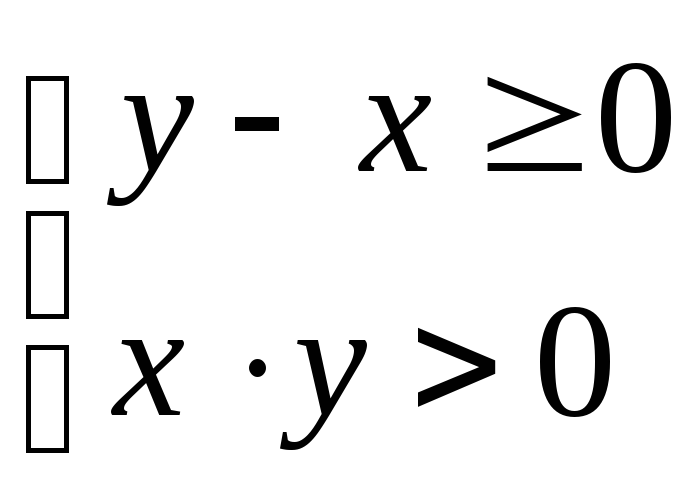. Неравенства и меняют свой знак на противоположный (соответственно) при пересечении следующих линий: x = y и x = 0, y = 0. Эти линии разбивают плоскость xOy на Рис. 9.2 6 областей. Последовательно, подставляя произвольные точки, из каждой области в систему 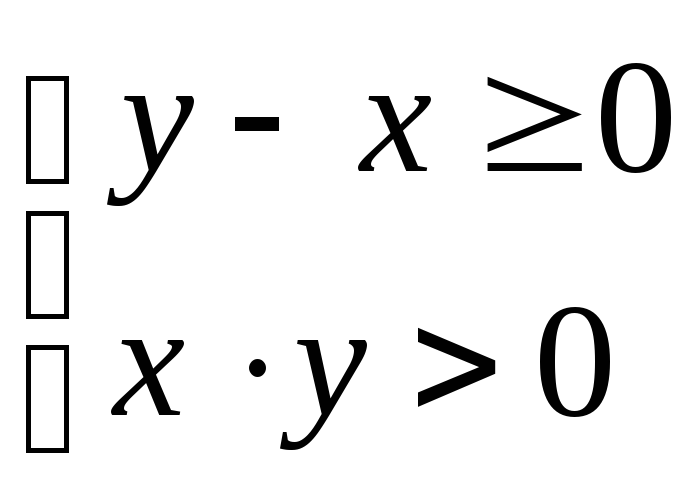, убеждаемся в том, что объединение областей (1) и (3) является областью определения исходной функции. Причем прямая x = y, за исключением точки (0; 0), входит в область определения, а прямые x = 0, и y = 0 – не входят (рис. 9.2).

 Замыканием области называется множество точек пространства , в любой окрестности каждой из которых содержатся точки области D.

Пусть, например, D – некоторая открытая (граница не включается) область на плоскости xOy. Тогда замыкание области получится, если к области D присоединить ее границу Г ().

 Пусть в некоторой области D плоскости xOy задана функция , и пусть – некоторая точка замыкания области D (). Число А называется пределом функции в точке М₀, если для любого числа  > 0 найдется такое число δ > 0, что для всех точек , удаленных от точки М₀ меньше, чем на δ (), выполнено неравенство .

Предел функции двух переменных обозначается .

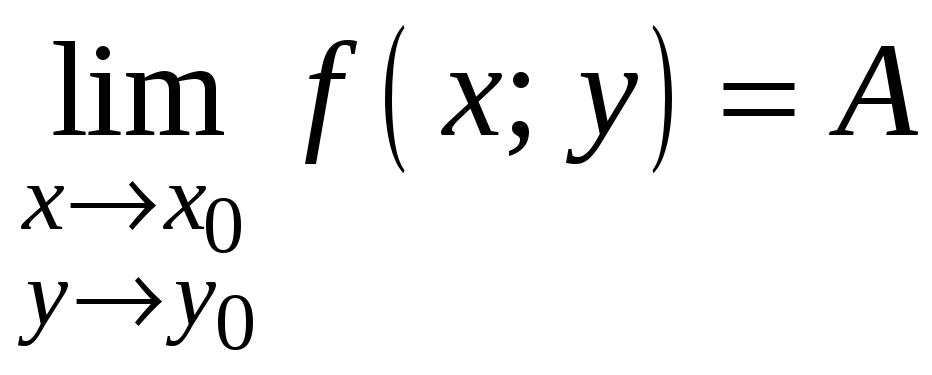 Функция называется непрерывной в точке если она определена в этой точке () и имеет место равенство .
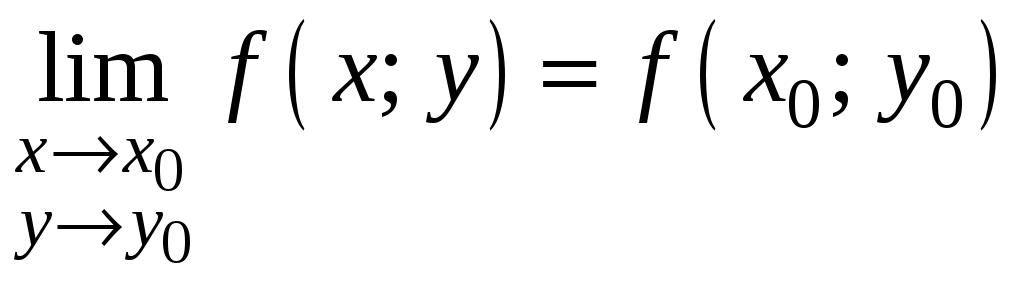