2. Вычисление длины дуги плоской кривой

 Предположим, что на плоскости некоторая дуга (кривая линия) является графиком непрерывно-дифференцируемой функции y = f(x) на отрезке [a; b] (рис. 8.1). В этом случае длину l дуги можно вычислить по формуле:

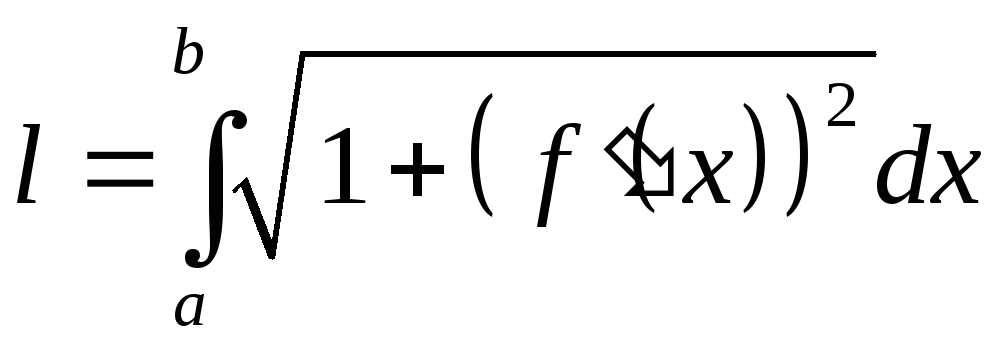. (8.14)

 Предположим, что дуга (рис. 8.1) является графиком функции, заданной параметрически 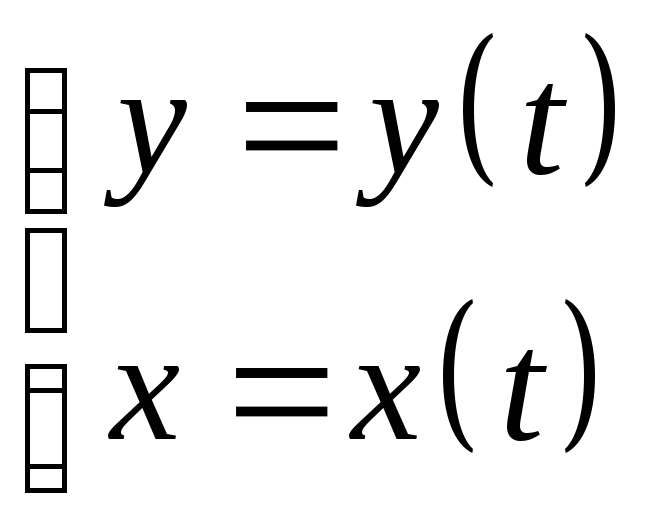на некотором отрезке [t₁; t₂], причем функции y(t) и x(t) непрерывно-дифференцируемы на данном отрезке. Тогда длину l дуги можно вычислить по формуле:

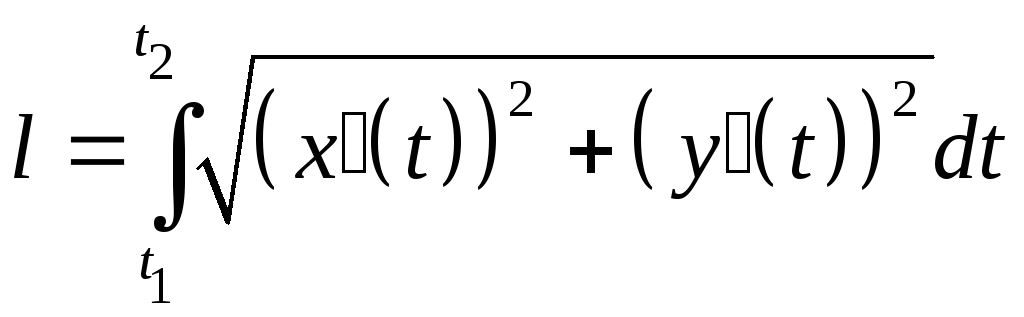. (8.15)

Пример 8.7. Вычислить длину дуги полукубической параболы на промежутке [0; 1] (рис. 8.5):

Р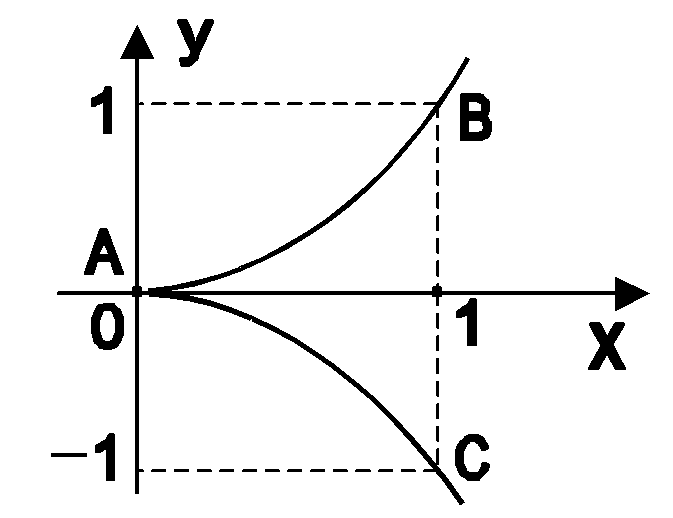ешение. Полукубическая парабола состоит из двух симметричных относительно оси OX ветвей . Искомая длина l равна сумме длин дуг (l₁) и (l₂). Так как длины дуг и совпадают, то l = 2l₁.

Таким образом, по формуле (8.14) мы получим

Рис 8.5.

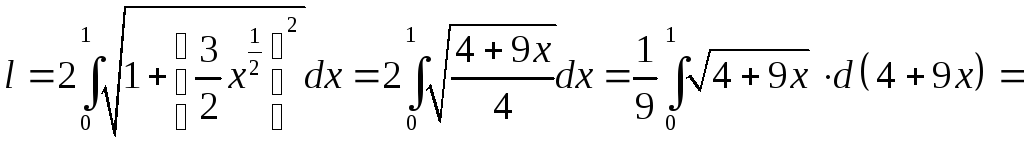
Пример 8.8. Вычислить длину астроиды 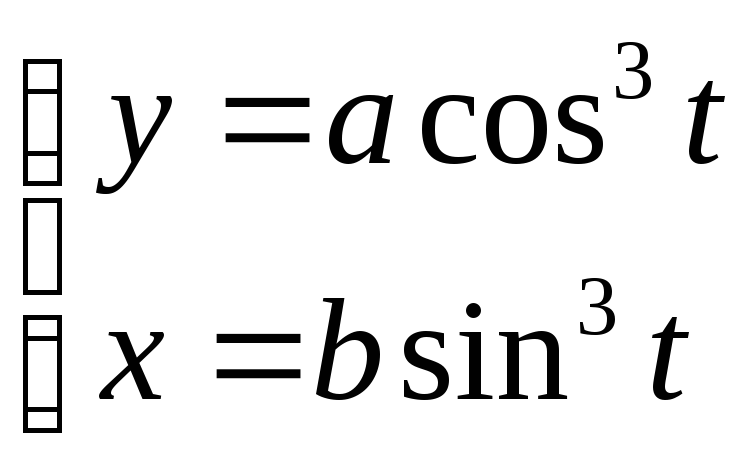(рис. 8.6):

Р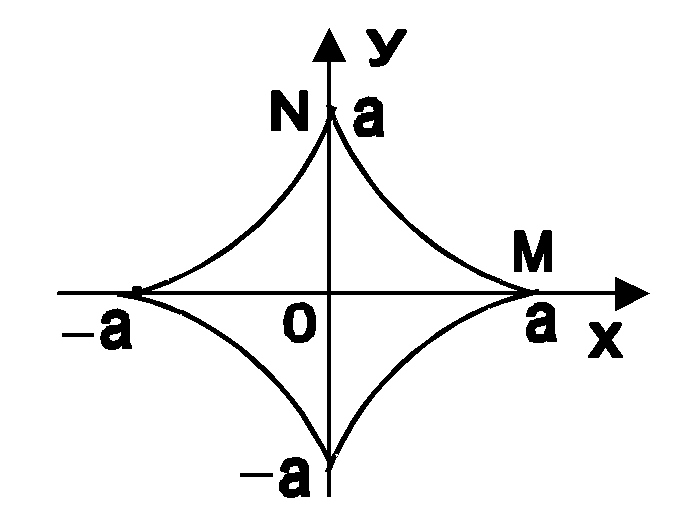ешение. Астроиду, так же как и циклоиду (пример 8.6) можно построить по точкам (в качестве упражнения сделайте это самостоятельно). Астроида состоит из четырех равных по длине частей. Найдем длину дуги астроиды, расположенной в первой четверти, и умножим ее на четыре. Началу дуги (точке M) соответствует значение параметра , концу дуги (точке N)

Рис 8.6. соответствует значение параметра .

Таким образом, по формуле (8.15) находим длину астроиды:

.

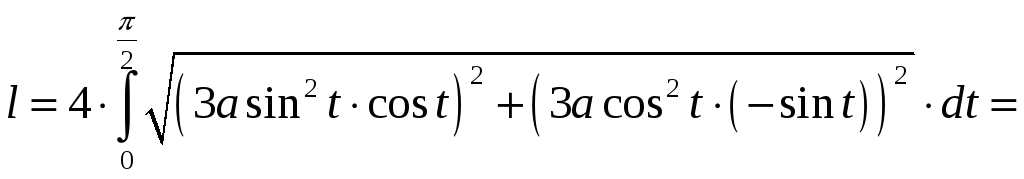
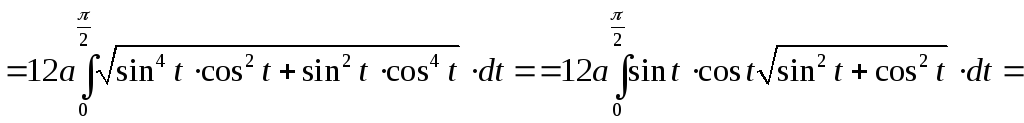
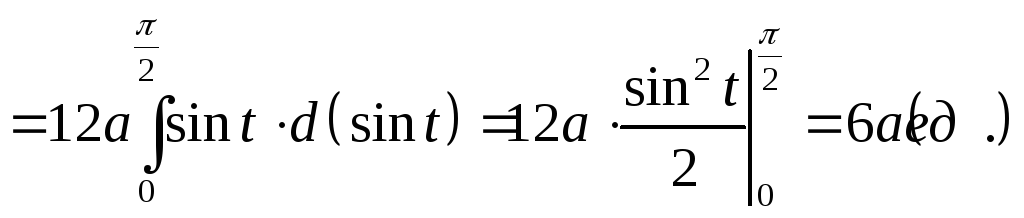3. Вычисление объема тела с известным поперечным сечением.

Предположим, что некоторое тело спроектировано на отрезок [a; b] числовой оси OX (рис. 8.7). Предположим, что в каждой точке x отрезка

[a; b] нам известна площадь S(x) поперечного сечения данного тела. Разобьем отрезок [a; b] точками на n частей и проведем в каждой из полученных точек плоскость, перпендикулярную оси OX. При достаточно большом числе разбиений отрезка [a; b], тело разрезается на большое Рис. 8.7. количество частей (слоев), каждую

из которых приближенно можно считать цилиндром. Высота i-го слоя (цилиндра) равна x_i = x_i – x_{i – 1}.

За площадь основания i-го цилиндра примем , где – произвольная точка i-го отрезка. Тогда объем i-го слоя приближенно равен , следовательно, объем тела равен

. (8.16)

Но сумма в формуле (8.16) является интегральной суммой для определенного интеграла 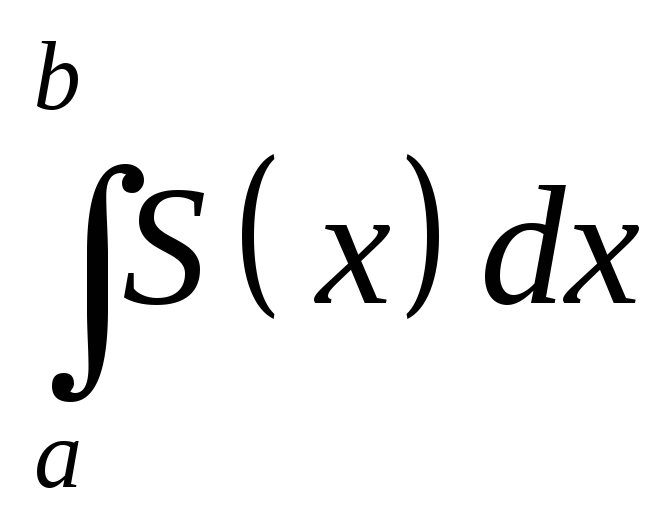. Таким образом, если функция S(x) является непрерывной на отрезке [a; b], то объем тела с известным поперечным сечением S(x) равен

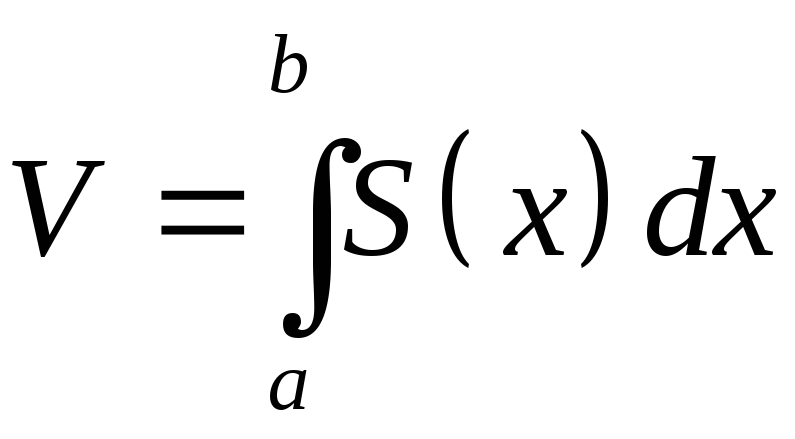. (8.17)

4. Вычисление объема тела вращения

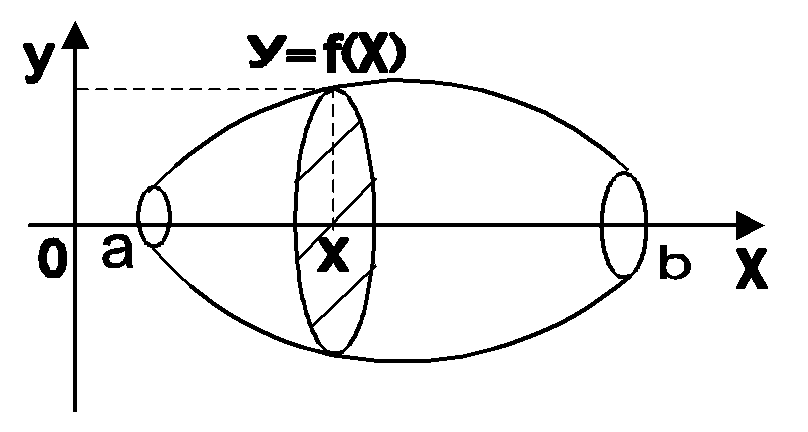
Предположим, что на промежутке [a; b] определена непрерывная функция y = f(x). Найдем объем тела, которое получается при вращении графика данной функции вокруг оси OX на данном промежутке. Любое сечение данного тела плоскостью, перпендикулярной оси OX, является кругом (рис. 8.8). Радиус круга в произвольной точке x[a; b] равен значению функции f(x) в этой точке. Следовательно, площадь круга равна Рис. 8.8. . Подставляя S(x) в формулу (8.17), мы получим формулу объема тела вращения:

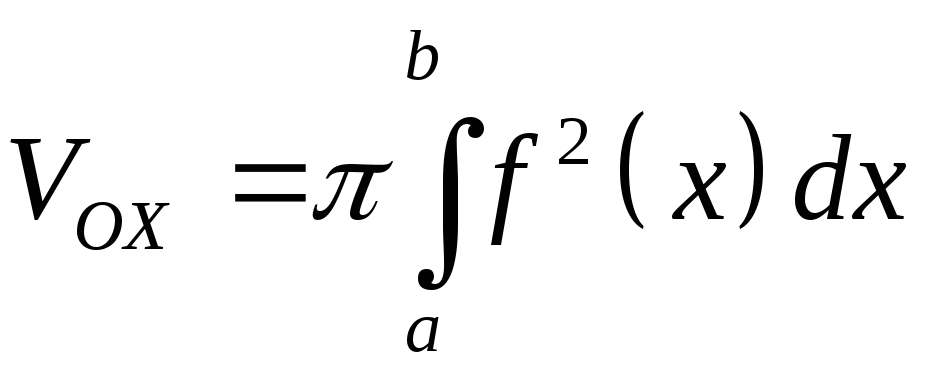. (8.18)

Пример 8.9. Вычислить объем веретена (рис. 8.9), полученного при вращении вокруг оси OX участка синусоиды, расположенного на промежутке [0;  ].

Решение. Искомый объем тела вращения найдем по формуле (8.18):

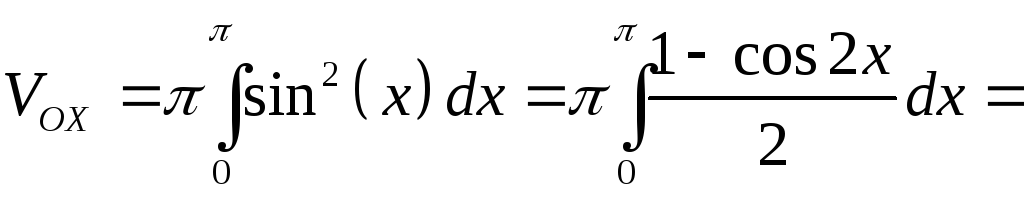
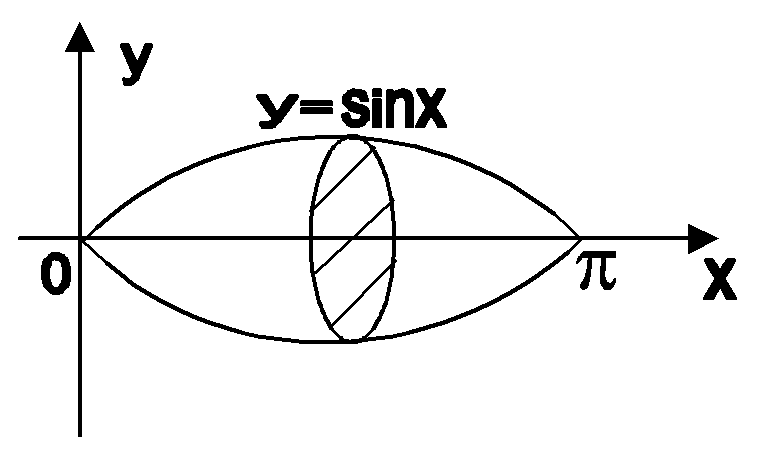Рис. 8.9.