
- •Преодоление дифракционного предела в оптическом диапазоне
- •Г л а в а 2. Плазменные возбуждения в объеме. Плазмоны и поляритоны
- •2.1. Квазичастицы в плазме
- •2.2. Поляритоны в диэлектрике
- •Г л а в а 3. Взаимодействие атомных структур с электромагнитными полями
- •3.1. Полуклассическая теория Бора
- •3.2. Принцип соответствия между классической и квантовой физикой
- •3.3. Сила осциллятора атомного перехода
- •Силы осцилляторов для атома водорода
- •3.4. Динамическая поляризуемость атома
- •3.5. Поглощение и рассеяние света атомом
- •Г л а в а 4. Электромагнитное излучение в среде
- •4.1. Уравнения Максвелла в среде
- •4.2. Линейный отклик среды на электромагнитное воздействие
- •4.3. Распространение электромагнитной волны в среде
- •4.4. Отражение и преломление электромагнитных волн
- •Г л а в а 5. Спектроскопия ближнего поля
- •5.1. Электромагнитное поле в дальней и ближней зонах
- •5.2. Зависимость от расстояния до источника полей в дальней и ближней зонах
- •5.3. Сканирующая оптическая микроскопия ближнего поля
- •Г л а в а 6. Поверхностные плазмоны
- •6.1. Поверхностные плазменные колебания
- •6.2. Определение и закон дисперсии поверхностных плазмонов
- •6.3. Генерация поверхностных плазмонов
- •6.4. Применение поверхностных плазмонов. Транспорт излучения через наноструктуры
- •Г л а в а 7. Метаматериалы
- •7.1. Отрицательное преломление
- •7.2. Электромагнитные процессы в «левой» среде
- •7.3. Композитные материалы с отрицательным преломлением
- •7.4. Другие типы метаматериалов
- •Литература
2.2. Поляритоны в диэлектрике
Рассмотрим теперь другой тип связанного электрон-фотонного возбуждения (или квазичастицы), которое может распространяться в твердом теле. В этом возбуждении, называемом поляритоном, вектор напряженности электрического поля перпендикулярен волновому вектору, т.е. соответствующая волна является поперечной. Как известно, в поперечной электромагнитной волне присутствуют оба поля: электрическое и магнитное, причем при распространении в вакууме их амплитуды равны. Этим поляритон отличается от плазмона, с которым связано только продольное электрическое поле.
Из уравнений Максвелла следует следующий закон дисперсии для поперечной электромагнитной волны:
![]() ,
(2.9)
,
(2.9)
где
![]() – поперечная часть диэлектрической
проницаемости среды, зависящая от
частоты (частотная дисперсия) и волнового
вектора (пространственная дисперсия).
Ясно, что, как и в случае продольной
волны, для определения закона дисперсии
поперечного электромагнитного возмущения
необходимо знать явный вид функции
– поперечная часть диэлектрической
проницаемости среды, зависящая от
частоты (частотная дисперсия) и волнового
вектора (пространственная дисперсия).
Ясно, что, как и в случае продольной
волны, для определения закона дисперсии
поперечного электромагнитного возмущения
необходимо знать явный вид функции![]() ,
который, вообще говоря, неизвестен.
Поэтому воспользуемся модельной
диэлектрической проницаемостью вещества
следующего вида:
,
который, вообще говоря, неизвестен.
Поэтому воспользуемся модельной
диэлектрической проницаемостью вещества
следующего вида:
![]() .
(2.10)
.
(2.10)
Модель (2.10)
предполагает, что основной частотно-зависимый
вклад в диэлектрическую проницаемость
дает одно квантовое возбуждение среды
с собственной частотой
![]() и силой осциллятора
и силой осциллятора![]() .
Это возбуждение может быть связано,
например, с электронным переходом в
примесных центрах, концентрация которых
.
Это возбуждение может быть связано,
например, с электронным переходом в
примесных центрах, концентрация которых![]() определяет плазменную частоту,
фигурирующую в правой части равенства
(2.10):
определяет плазменную частоту,
фигурирующую в правой части равенства
(2.10):![]() .
Не зависящее от частоты слагаемое
.
Не зависящее от частоты слагаемое![]() связано с вкладом в диэлектрическую
проницаемость основного вещества. В
модели (2.10) пренебрежено пространственной
дисперсией диэлектрической проницаемости,
что оправдано для случая примесного
центра в твердом теле, размер которого
много меньше, чем длина волны
рассматриваемого возбуждения.
связано с вкладом в диэлектрическую
проницаемость основного вещества. В
модели (2.10) пренебрежено пространственной
дисперсией диэлектрической проницаемости,
что оправдано для случая примесного
центра в твердом теле, размер которого
много меньше, чем длина волны
рассматриваемого возбуждения.
Решение уравнения (2.9) с диэлектрической проницаемостью (2.10) дает две дисперсионные зависимости для поперечных электромагнитных волн в среде:
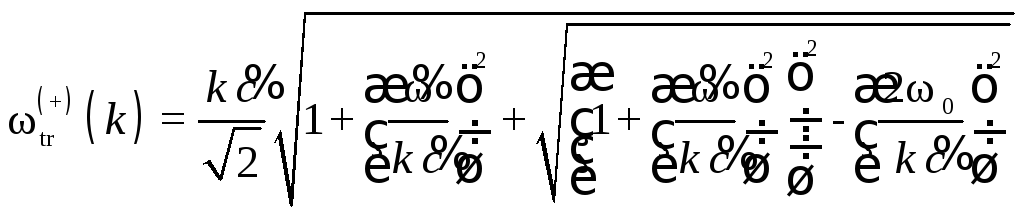 ,
(2.11)
,
(2.11)
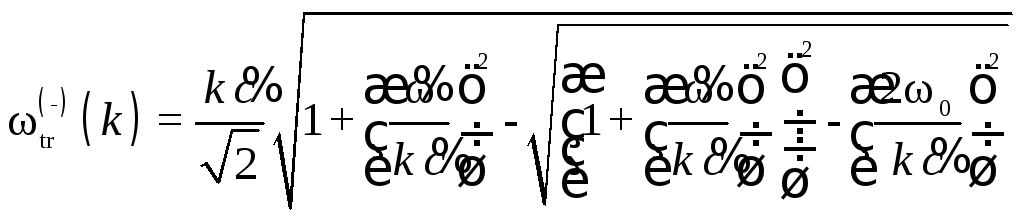 ,
(2.12)
,
(2.12)
где
![]() и
и![]() .
.
Графики функций
(2.11) – (2.12) приведены на рис. 2.2 для
следующих значений параметров:
![]() ,
,![]() ,
,![]()
![]() ,
тогда
,
тогда![]() и
и![]() .
.
Из рис. 2.2 видно,
что асимптотами дисперсионных кривых
являются прямые 3, 4 и 5. Зависимость 3
представляет собой линейный закон
дисперсии в среде без квантового
возбуждения. Линия 4 описывает квантовое
возбуждение среды и не зависит от
волнового вектора излучения. Наконец,
прямая 5 соответствует частоте
![]() ,
которая включает в себя эффект
перенормировки энергии квантового
возбуждения среды за счет взаимодействия
с электромагнитным полем. Чем больше
это взаимодействие, пропорциональное
разности
,
которая включает в себя эффект
перенормировки энергии квантового
возбуждения среды за счет взаимодействия
с электромагнитным полем. Чем больше
это взаимодействие, пропорциональное
разности![]() ,
тем сильнее отличие дисперсионных
кривых от ломаных прямых линий.
,
тем сильнее отличие дисперсионных
кривых от ломаных прямых линий.
Таким образом, законы дисперсии поперечных электромагнитных волн (2.11) – (2.12) описывают макроскопическое электромагнитное поле, связанное с квантовым возбуждением среды.
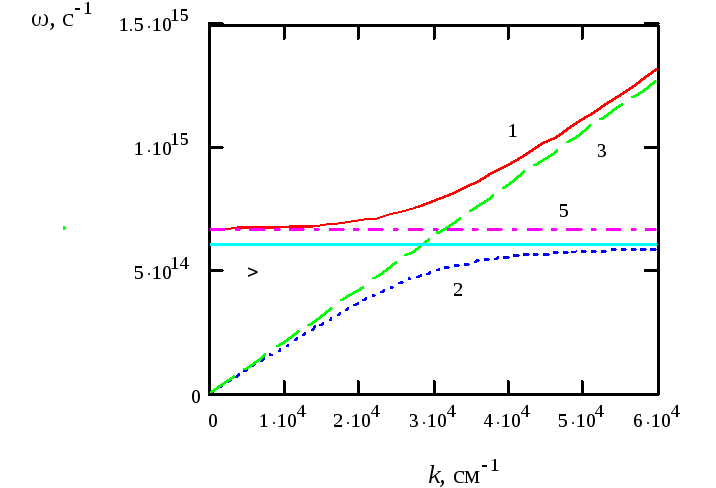 Рис.
2.2. Дисперсия поперечных волн в среде
при наличии одного квантового возбуждения:
1 –
Рис.
2.2. Дисперсия поперечных волн в среде
при наличии одного квантового возбуждения:
1 –
![]() ;
2 –
;
2 –![]() ;
3 –
;
3 –![]() ;
4 –
;
4 –![]() ;
5 –
;
5 –![]()
Существенно, что групповая скорость поляритона на верхней дисперсионной ветви стремится к нулю с уменьшением волнового вектора, а групповая скорость на нижней дисперсионной кривой стремится к нулю в пределе больших волновых векторов (см. рис. 2.2). Это говорит о том, что верхняя кривая в пределе малых длин волн описывает фотон в среде, а в пределе длинных волн – возбуждение примесного центра. Нижняя кривая, наоборот, для больших длин волн отвечает фотону в среде, а для малых длин волн соответствует возбуждению примесного центра.
Важно отметить,
что в частотном интервале
![]() распространяющееся макроскопическое
поле отсутствует, поскольку в нем
диэлектрическая проницаемость среды
отрицательна. Таким образом, промежуток
распространяющееся макроскопическое
поле отсутствует, поскольку в нем
диэлектрическая проницаемость среды
отрицательна. Таким образом, промежуток![]() может быть названполяритонной
запрещенной зоной
по аналогии с энергетическим спектром
электронов в твердом теле.
может быть названполяритонной
запрещенной зоной
по аналогии с энергетическим спектром
электронов в твердом теле.
