4.3. Распространение электромагнитной волны в среде

Рассмотрим монохроматическое излучение, напряженность электрического и магнитного поля в котором представляет собой плоскую волну:

, (4.28)

, (4.29)

где и– комплексные амплитуды напряженностей электрического и магнитного полей. Подставляя выражения (4.28) – (4.29) в уравнения Максвелла (4.6) – (4.7) и (4.15) – (4.16), получаем систему алгебраических уравнений для комплексных амплитуд электромагнитного поля:

, (4.30)

, (4.31)

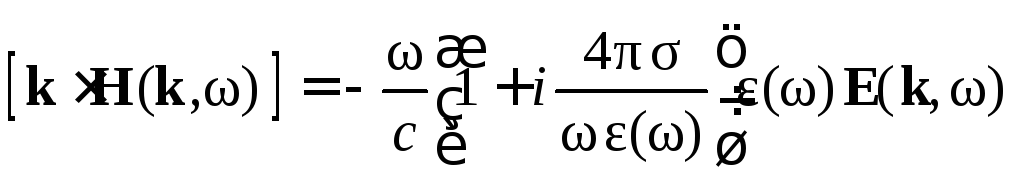, (4.32)

. (4.33)

Если выполняется неравенство

, (4.34)

то можно пренебречь вторым слагаемым в круглых скобках правой части равенства (4.32) по сравнению с единицей, и вместо (4.32) получаем

. (4.35)

Условие (4.34) является критерием «диэлектричности» среды, что соответствует пренебрежению током проводимости по сравнению с током смещения. В противоположном пределе, когда среда является проводником, из уравнения (4.32) находим

. (4.36)

Рассмотрим сначала случай диэлектрической среды. Исключая из уравнений (4.30) и (4.35) напряженность магнитного поля, получаем алгебраическое уравнение на комплексную амплитуду электрического поля в плоской волне:

. (4.37)

При выводе левой части этого равенства была использована известная формула для двойного векторного произведения: .

Пусть вектор напряженности электрического поля перпендикулярен волновому вектору, т.е. имеет место случай поперечного поля . Тогда уравнение (4.37) дает

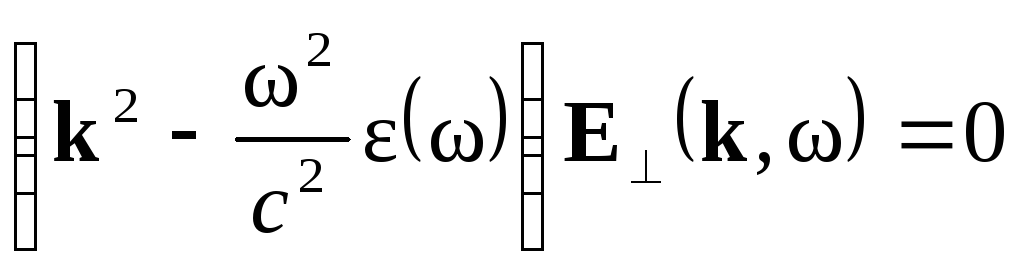. (4.38)

Отсюда получаем закон дисперсии поперечных электромагнитных волн в диэлектрической среде:

. (4.39)

Как видно из последнего равенства, волновой вектор электромагнитного поля в среде, вообще говоря, есть комплексная величина: . В дальнейшем предполагаем, что, тогда можно записать:

, . (4.40)

Здесь введены действительная и комплекснаячасти показателя преломления средыс учетом их зависимости от частоты. Подставляя (4.40) в (4.39) и отделяя действительную и мнимую части, получаем следующую систему уравнений для действительной и мнимой частей комплексного показателя преломления:

, (4.41)

. (4.42)

Решение системы (4.41) – (4.42) имеет вид

, (4.43)

. (4.44)

Если, как это часто бывает в случае диэлектрической среды, и, то решение (4.43) – (4.44) приближенно равно

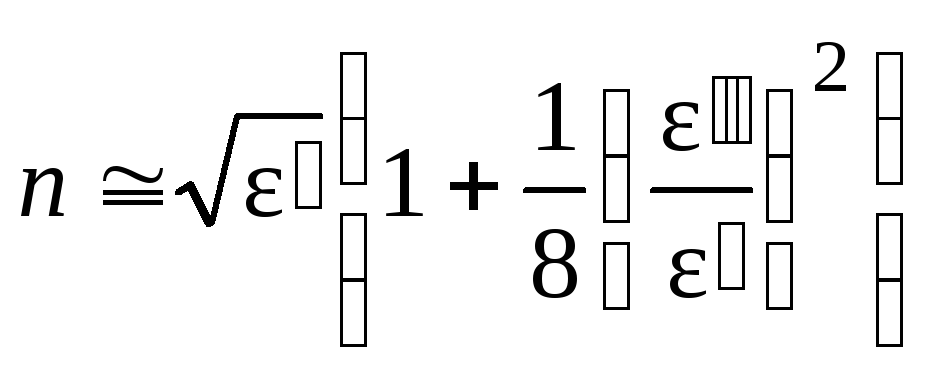, (4.45)

. (4.46)

Итак, в случае малой величины мнимой части диэлектрической проницаемости комплексный показатель преломления среды дается приближенными равенствами (4.45) – (4.46).

Подставляя волновой вектор (4.40) в уравнение (4.30), находим для комплексной амплитуды напряженности магнитного поля:

. (4.47)

Из этого равенства вытекает соотношение между амплитудами и фазами напряженностей электрического и магнитного полей в среде.

Из равенства (4.28) с учетом выражения для волнового вектора (4.40) находим для напряженности электрического поля в плоской волне, распространяющейся в среде:

, (4.48)

где предположено, что , т.е. электромагнитная волна распространяется в положительном направлении оси. Из полученного выражения (4.48) следует, что фазовая скорость плоской волны в среде с показателем преломленияравна

, (4.49)

если же , то, как это видно из формулы (4.48), исчезает зависимость фазы поля от координаты.

Поскольку интенсивность излучения пропорциональна квадрату модуля напряженности электрического поля, то для зависимости интенсивности от координаты(в направлении распространения излучения) можно получить следующее выражение:

, (4.50)

т.е. имеет место затухание излучения с коэффициентом экстинкции (extinction) , равным

. (4.51)

Случай диэлектрической среды и проводника можно рассматривать единообразно, если произвести следующую замену диэлектрической проницаемости:

. (4.52)

Для металлов справедливо неравенство, обратное к (4.34), в таком случае, принимая во внимание замену (4.52), можно считать, что

и . (4.53)

В этом случае из (4.43) – (4.44) следует

. (4.54)

Затухание электромагнитной волны при распространении в среде не обязательно связано с истинным поглощением энергии поля, чему соответствует наличие мнимой части у диэлектрической проницаемости. Коэффициент , описывающий затухание интенсивности согласно (4.50), может быть не равен нулю и при, если только. Тогда из уравнений (4.41) – (4.42) следует, чтои. Такая ситуация имеет место при отражении излучения от плазмы, когда для частотдиэлектрическая проницаемость плазмы является действительной отрицательной величиной (см. формулу (4.27)). Если же, то диэлектрическая проницаемость плазмы (4.27) – действительная положительная величина, так что излучение распространяется в плазме без ослабления. Такая ситуация имеет место при прохождении ультрафиолетового излучения через металлы –ультрафиолетовая прозрачность металлов. Дело в том, что в металлах вклад электронов проводимости, обладающих нулевыми собственными частотами, в диэлектрическую проницаемость как раз описывается плазменной формулой (4.27). Отражение излучения видимого диапазона от металлов связано с тем, что плазменная частота (4.27) для электронов проводимости лежит выше частотной границы видимого и ультрафиолетового спектров излучения.

Запишем выражение для вектора Пойтинга в среде:

, (4.55)

где и– действительные напряженности полей. Модуль вектора Пойтинга равен интенсивности электромагнитного излучения, т.е. количеству энергии поля, протекающему в единицу времени через единицу площади. Формула (4.55) совпадает с выражением для вектора Пойтинга в вакууме с той разницей, что в (4.55) фигурируют макроскопические поля в среде, так что связь между напряженностью магнитного и электрического полей дается формулой (4.47). Интенсивность монохроматического поля в среде с учетом сказанного равна

, (4.56)

где – действительная амплитуда напряженности электрического поля в монохроматическом излучении заданной частоты.

Вычислим дивергенцию от вектора Пойтинга (4.55), воспользовавшись уравнениями Максвелла в среде (4.6), (4.15) и формулой векторного анализа . В результате, предполагая, что свободные заряды отсутствуют, получим следующее выражение:

. (4.57)

Поскольку левая часть равенства (4.57) описывает изменение энергии электромагнитного поля за счет выхода излучения за границу выделенного объема, (что следует из формулы ГауссаОстроградского), то правую часть равенства (4.57) можно отождествить с изменением энергии электромагнитного поля в единицу времени в единичном объеме. Иными словами, величина

(4.58)

представляет собой мгновенную мощность электромагнитного поля в единице объема, связанную с уменьшением или увеличением энергии поля.

Вычислим с помощью формулы (4.58) среднюю за период мощность, рассеиваемую монохроматическим излучением в среде. Для этого выразим действительные функции времени, фигурирующие в правой части равенства (4.58), через соответствующие комплексные величины по формуле

(4.59)

и воспользуемся формулой (4.18) для электрической индукции. После усреднения по периоду поля останутся отличными от нуля только произведения величин, содержащих комплексно-сопряженные мнимые экспоненты. В результате для мощности в единице объема получаем следующее выражение:

. (4.60)

Итак, мощность монохроматического излучения, поглощаемая в среде, пропорциональна мнимой части диэлектрической проницаемости (или восприимчивости) вещества. (Магнитные среды, в которых и, мы не рассматриваем.)

Подчеркнем, что поглощение имеет место, если . Эти неравенства всегда справедливы для термодинамически равновесной среды в силу закона возрастания энтропии. В случае же термодинамически неравновесной (инвертированной) среды данные неравенства могут иметь обратный знак, тогда электромагнитное излучение будетусиливаться средой.

Определим условия усиления излучения, когда для диэлектрической проницаемости среды справедливо выражение (4.26). Для простоты рассмотрим вклад в восприимчивость атомов одного типа. Обобщим выражение для динамической поляризуемости основного состояния атома (3.48) на случай атома, находящегося в m-м состоянии:

. (4.61)

Тогда с учетом заселенности m-го состояния атома для восприимчивости среды имеем выражение

, , (4.62)

где – полная концентрация атомов. Пусть частота электромагнитного излучения близка к одной из собственных частот атома:

, , (4.63)

причем – дипольно-разрешенный переход, т.е.. Тогда из формул (4.61), (4.62) следует выражение для резонансной восприимчивости среды:

. (4.64)

При выводе формулы (4.64) было использовано равенство

, (4.65)

которое следует из соотношения между силами осцилляторов взаимно обратных переходов: . С помощью формул (4.61) и (4.64) и выражения для силы осциллятора (3.39) находим для мнимой части резонансной восприимчивости среды:

, (4.66)

где – спектральная форма линии, которая в случае однородно уширенного перехода дается формулой (3.61).

Таким образом, условие усиления резонансного излучения в среде имеет вид

при . (4.67)

Выполнение этого критерия означает инвертированность среды, а величина называетсяинверсией населенности.

Отношение мощности электромагнитного излучения, выделяемой (диссипируемой) в единице объема среды, к интенсивности излучения имеет размерность обратной длины и называется коэффициентом усиления (поглощения):

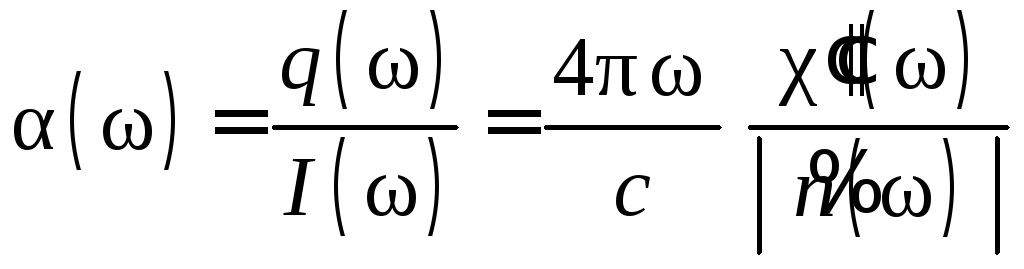. (4.68)

Заметим, что это выражение совпадает с формулой (4.51) для коэффициента экстинкции, если в нем положить , что соответствует предположению, сделанному при выводе (4.51). В резонансных условиях (4.63) с помощью формулы (4.66) находим для коэффициента усиления (поглощения) монохроматического электромагнитного поля в среде:

, (4.69)

где – сечение резонансного перехода:

. (4.70)

Таким образом, как это следует из полученных выражений (4.68) – (4.70), резонансное излучение в среде усиливается, если имеет место инверсия населенностей (4.67) на активном переходе . В противном случае, излучение будет ослабляться за счет поглощения на этом переходе.