все

Задача 1. Система состоит из N >> 1 независимых частиц, каждая из которых может находиться в одном из двух квантовых состояний с энергиями – и . Определить энтропию S состояния с энергией Определить температуру Т этого состояния. Вычислить энтропию при Т = 0. Найти равновесное число частиц в верхнем состоянии, а также равновесную энергию и теплоемкость как функции температуры Т.

Решение. Пусть 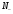- число частиц на нижнем уровне двухуровневой системы, а - число частиц на верхнем уровне, так что Энергия всей системы тогда равна Следовательно, Такое состояние можно достичь

(1)

способами (число сочетаний). Это – статистический вес состояния с энергией Е. Энтропия системы равна логарифму статистического веса (числа состояний): Согласно формуле Стирлинга для больших чисел

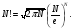(2)

Пренебрегая фактором , получим для энтропии

. (3)

Статистическая температура определяется соотношением

(4)

Подставляя (3) в (4), находим:

(5)

Должно быть Т > 0 (нормальная система): в противном случае статистическая сумма обратится в бесконечность. Следовательно, согласно (5) должно быть n < 0. Если , то согласно (5) При этом все частицы находятся на нижнем уровне (одно квантовое состояние). Согласно (3) при этом энтропия стремится к нулю (теорема Нернста). Далее, из (5) находим равновесное число частиц на верхнем уровне

(6)

Этот же результат можно получить независимо и из распределения Гиббса 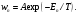Рассмотрим одну частицу, которая может находиться на нижнем или на верхнем уровнях. В данном случае энергия квантового состояния для верхнего уровня , а нормировочный множитель .

Из (6) далее определяем энергию при заданной температуре Т:

(7)

Наконец, из (7) находим теплоемкость:

(8)

На рис. 1 представлен согласно (7) график в зависимости от величины . При большой температуре эта энергия стремится к нулю (равнозаселенность уровней). Напротив, при нулевой температуре энергия равна (все частицы на нижнем уровне).

>

Рис. 1.

На рис. 2 представлен график C/N в зависимости от величины . Видно, что теплоемкость (так называемая теплоемкость Шоттки) содержит резкий (и неочевидный) максимум при значении вблизи единицы.

>

_{Рис. 2.}

Задача 2. Найти теплоемкость идеального одноатомного газа, помещенного в гравитационное поле в сосуде высотой h.

Решение. Энергия атома в гравитационном поле имеет вид

(1)

Вычисляем классическую статистическую сумму сначала для одного атома. Координатная часть ее имеет вид

(2)

Здесь - площадь сосуда.

Импульсная часть статистической суммы равна

(3)

Итак,

. (4)

Статистическая сумма для N частиц равна (используя формулу Стирлинга)

(5)

Выразим свободную энергию через найденную статистическую сумму

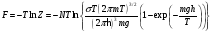. (6)

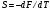Далее определим энергию системы Учитывая, что при фиксированном объеме , получим и Подставляя в это соотношение выражение (6) для свободной энергии, находим

(7)

Теплоемкость при постоянном объеме определяется как

. (8)

Если , из (8) следует, что Если, наоборот, , то из (8) следует, что В последнем случае это означает, что гравитационными силами можно пренебречь. При увеличении высоты сосуда теплоемкость растет, так как растет потенциальная энергия атомов.

На рис. 1 представлена зависимость как функция 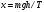согласно (8). Видно, что выход на значение достигается при достаточно большом значении параметра > 10.

>

Рис. 1.

Задача 3. Классический газ магнитных диполей находится в магнитном поле Н при температуре Т. Найти намагниченность М и магнитную восприимчивость .

Решение. Нас интересует только координатная часть статистической суммы, так как импульсная часть не зависит от магнитного поля. Энергия магнитного диполя в магнитном поле равна . Статистическая сумма для одного диполя равна

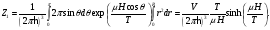(1)

Здесь - объем, в котором находится диполь. Статистическая сумма для N диполей равна . Свободная энергия равна

. (2)

Намагниченность (магнитный момент единицы объема среды) определяется по формуле , так как именно свободная энергия определена при заданной температуре и объеме. При этом N - число диполей в единице объема. Из (2) получим

(3)

Магнитная восприимчивость определяется как 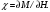Подставляя (3), находим

(4)

В слабом магнитном поле, из (4) получим Напротив, в сильном магнитном поле, из (4) получим При этом согласно (3) , т.е. все диполи выстраиваются вдоль магнитного поля. График функции в зависимости от безразмерного параметра согласно (4) представлен на рис. 1.

>

Рис. 1.

Задача 4. Идеальный газ атомов с полным моментом J, спином S и орбитальным моментом L помещен в слабое магнитное поле с напряженностью Н, так что температура и расщепление уровней в магнитном поле малы по сравнению с энергетическим расстоянием от основного состояния до ближайшего возбужденного состояния. Найти магнитную восприимчивость и исследовать случаи и Найти также изменение температуры при адиабатическом выключении магнитного поля от Н до нуля.

Решение. Энергия атома в слабом магнитном поле равна

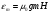. (1)

Здесь - магнетон Бора, фактор Ланде

,

m – проекция полного момента J на направление магнитного поля, Статистическая сумма для одного атома имеет вид

(2)

Вычисляем эту сумму (геометрическая прогрессия)

. (3)

Статистическая сумма для N атомов равна Подставляя (3), находим свободную энергию Получим

. (4)

Намагниченность (магнитный момент единицы объема) равна (N – тогда число атомов в единице объема). Подставляя (4), находим

. (5)

При (сильное магнитное поле) отсюда получим (все атомы выстроены вдоль магнитного поля). Если, напротив, (слабое магнитное поле), то из (5) следует, что

. (6)

Таким образом, газ парамагнитен, а восприимчивость обратно пропорциональна температуре (закон Кюри).

В общем случае восприимчивость 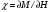согласно (5) равна

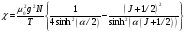. (7)

В сильном магнитном поле отсюда получим экспоненциально малую восприимчивость

(8)

На рис. 1 показан график восприимчивости в зависимости от согласно выражению (7) при J = 2. Значение при Н = 0 соответствует выражению (6).

>

Рис. 1.

Теперь обратимся ко второй части задачи. При адиабатическом процессе сохраняется энтропия, т.е. Вычислим энтропию, используя выражение (4) для свободной энергии:

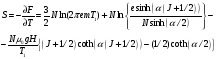(9)

Здесь был добавлен еще вклад энтропии кинематического движения свободного атома в отсутствие магнитного поля. Соответствующий вклад в статистическую сумму равен 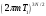, а в свободную энергию: Величина .

При Н = 0 энтропия принимает вид

(10)

Приравнивая величины (9) и (10) друг другу, находим

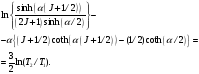(11)

Отсюда находим окончательно связь между температурами

(12)

Как должно быть, при Н = 0 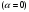отсюда получим, что Температура не меняется и в присутствии магнитного поля, но при J = 0. Это также очевидно. Если , то из (12) следует простое соотношение

(13)

На рис. 2 представлена зависимость (12) как функция снова для случая J = 2.

>

Рис. 2

Видно, что имеет место охлаждение газа, причем в случае сильного магнитного поля (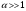) выполняется простое соотношение (13).

Задача 5. Определить разность теплоемкостей в переменных а) V,T; б) P,T. Определить для а)идеального больцмановского газа: б) газа Ван-дер-Ваальса; в) идеального вырожденного ферми-газа при ; г) фотонного газа.

Решение. По определению

Итак,

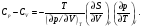(1)

Упрощаем правую часть этого соотношения, используя выражение для дифференциала свободной энергии . Следовательно,

(2)

Подставляя это соотношение в (1), окончательно находим

(3)

Теперь рассмотрим примеры.

а) уравнение Клапейрона для идеального газа имеет вид Следовательно,

Подставляя эти соотношения в (3), находим простое хорошо известное соотношение

(4)

б) уравнение Ван-дер-Ваальса имеет вид

Следовательно,

Подставляя эти соотношения в (3), находим

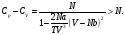(5)

Отметим, что при а = 0 отсюда получим снова соотношение (3) для идеального газа, хотя b может быть отлично от нуля.

в) перепишем (3) с учетом (2) в виде

(6)

Энтропия газа Ферми при равна

Уравнение состояния газа Ферми при имеет вид

Подставляя эти соотношения в (6), находим малое отличие между теплоемкостями, кубичное по температуре:

(7)

г) фотонный газ (черное излучение). Уравнение состояния имеет вид

Так как , а конечно, то согласно (3) имеем При этом теплоемкость является конечной, а - бесконечной величиной.

д) повторяем рассуждения раздела а) с заменой давления на объем и наоборот:

Итак,

(8)

Для термодинамического потенциала имеем Следовательно,

Подставляя это соотношение в (8), окончательно находим

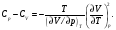(9)

Задача 6. Найти колебательную и вращательную теплоемкости двухатомных молекул, составленных из разных атомов. Исследовать случаи высоких и низких температур.

Решение. Начнем с вращения двухатомных молекул. Энергия вращения имеет вид

Здесь I – момент инерции молекулы, K – вращательное квантовое число. Вращательные уровни вырождены (2K + 1) раз. Вращательная статистическая сумма для одной молекулы имеет вид

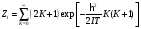(1)

Аналитически она не вычисляется. Для N молекул вращательная статистическая сумма имеет вид Соответствующая свободная энергия равна

Обычная энергия Е определяется как Получаем (для одной молекулы) для энергии и вращательной теплоемкости:

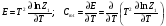(2)

График вращательной теплоемкости показан на рис. 1 в зависимости от безразмерного параметра

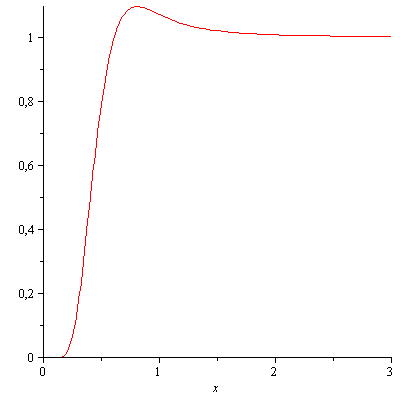
Рис. 1.

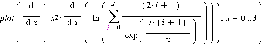
Видно, что вращательная теплоемкость на определенном участке превышает единицу, но стремится к ней при высоких температурах.

Аналитически можно найти теплоемкость при низких и высоких температурах. При низких температурах, когда , оставляем в статистической сумме только два слагаемых В том же приближении свободная энергия равна Вращательная теплоемкость )в расчете на одну молекулу) получается равной

(3)

В случае высоких температур, когда , для вычисления статистической суммы используем формулу Эйлера-Маклорена

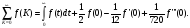
В применении к (1) получим (сохраняя члены 1/x << 1)

Следовательно, свободная энергия имеет вид

Обычная энергия равна

Окончательно для вращательной теплоемкости получим (в расчете на одну молекулу)

(4)

Отсюда следует, что она стремится к единице сверху, как это видно из рис. 1.

Теперь обратимся к колебательной части теплоемкости. Квантовая энергия гармонических колебаний имеет вид

Колебательная статистическая сумма вычисляется элементарно (для одной молекулы)

Свободная энергия равна (для N молекул)

.

Обычная энергия равна

Для колебательной теплоемкости находим (в расчете на одну молекулу)

(5)

Ее график как функция безразмерного параметра представлен на рис. 2.

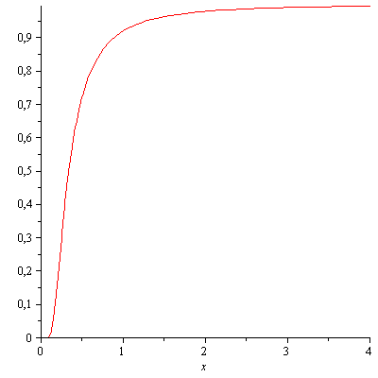
Рис. 2.

При низких температурах 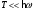теплоемкость согласно (5) экспоненциально мала

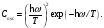
Напротив, при высоких температурах согласно (5) она стремится снизу к единице по закону

.

Задача 7. Найти температурную зависимость вращательной теплоемкости молекул параводорода и ортоводорода.

Решение. В молекуле водорода электронные спины всегда взаимно компенсируются, так что суммарный электронный спин равен нулю. Для молекулы параводорода суммарный ядерный спин равен нулю, а для молекулы ортоводорода – единице. Следовательно, спиновая ядерная волновая функция параводорода антисимметрична, в то время как спиновая ядерная волновая функция ортоводорода – симметрична. Чтобы полная волновая функция была бы антисимметрична в соответствии с принципом Паули, надо, чтобы координатная ядерная волновая функция параводорода была бы симметрична относительно перестановки протонов, т.е. поворота молекулы на 180 градусов, а ортоводорода – антисимметрична. Это вытекает из того факта, что волновые функции сферического ротатора представляют собой шаровые функции, которые и обладают указанной четностью при повороте на 180 градусов. Таким образом, четные вращательные квантовые числа соответствуют симметричным координатным волновым функциям, т.е. они реализуются для параводорода. Напротив, для ортоводорода реализуются нечетные вращательные квантовые числа.

В соответствии со сказанным запишем вращательную статистическую сумму для молекулы параводорода в виде (см. формулу (1) в задаче 6):

(1)

Соответственно для теплоемкости получим (см. формулу (2) в предыдущей задаче 6)

(2)

Ее вид как функция безразмерного параметра 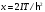показан на рис. 1.

Рис. 1

Из этого рисунка следует неочевидный факт, что теплоемкость имеет максимум, превышающий единицу. При высокой температуре, 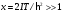, она сверху стремится к единице – классическому пределу, как и в случае разных атомов (задача 6).

Теперь обратимся к ортоводороду. Вращательная статистическая сумма имеет вид

(3)

Теплоемкость, рассчитанная по формуле (2), имеет вид, показанный на рис. 2, как функция безразмерного параметра .

Рис. 2.

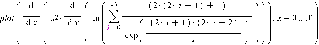
В отличие от параводорода здесь нет максимума, а теплоемкость монотонно растет, достигая единицы в классическом пределе высоких температур, .

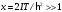Задача 8. Найти флуктуации величин

Решение. Рассмотрим замкнутую статистическую систему. Пусть в ней находится малая статистическая подсистема. В равновесии полную энтропию всей системы обозначим S₀. Она является функцией полной энергии всей системы. При малом отклонении подсистемы от равновесия (флуктуации) полная энтропия меняется на малую величину . При этом процессе идет обмен энергией между малой подсистемой и термостатом (оставшаяся часть всей системы). Таким образом,

Здесь величина относится к малой подсистеме. По определению , где - появившееся при флуктуации число состояний, w – вероятность указанной флуктуации, А – коэффициент пропорциональности. Итак,

.

Здесь мы опустили индекс 0, так как ввиду малости флуктуации значения температуры и давления для подсистемы и термостата совпадают друг с другом.

Рассматривая малое изменение энергии подсистемы как функцию ее энтропии и объема, разложим это изменение в ряд Тейлора

.

Первые два слагаемых являются знакопеременными при флуктуациях, и их можно опустить при усреднении по флуктуациям. Следовательно,

Перепишем это выражение в виде

Так как

то окончательно получим общую формулу для вероятности флуктуации

. (1)

Выберем в качестве независимых переменных V, T. Тогда

так как

. (2)

Далее, аналогично

.

Подставляя эти соотношения в (1), находим

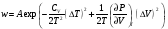
Так как произведение флуктуаций объема и температуры выпало из этого соотношения, то это означает, что указанные флуктуации являются независимыми друг от друга, т.е.

Каждая из флуктуаций описывается формулой Гаусса

(3)

Следовательно, находим:

(4)

Выберем теперь в качестве независимых переменных в (1) давление и энтропию. Тогда

Далее,

.

Так как дифференциал энтальпии равен 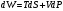, то

Следовательно,

.

Подставляя эти соотношения в (1), находим

Видно, что флуктуации давления и энтропии являются независимыми друг от друга. В соответствии с распределением Гаусса (3) отсюда находим