4.Экстремум функции двух переменных.
(·)M (x0,y0) – наз. (·) локального максимума функции f (x,y), если выполняется неравенство. f(x,y)≤f (x0,y0) (множества (х, у).єИδ(x0,y0) )(1). (·)M (x0,y0) – наз. (·) локального минимума функции f (x,y), если выполняется неравенство. f(x,y)≥f (x0,y0) (множества (х, у).єИδ(x0,y0) )(2). Максимум и минимум её функции наз. её экстремумом. (·)M (x0,y0) в которой достигается экстремум функции наз. (·) экстремума функции.
Теорема 1. (необходимое условие локального экстремума). Если (·)M (x0,y0) явл. (·)локального экстремума, то в этой (·)частной производной часто =0. ð f(x0,y0)/ðx = ð f(x0,y0)/ðy=0; или ходьбы одно из частных не сущ. (·) в которых частный производные = 0, наз. стационарными точками двух переменных функций. То есть если экстремум в (·) М достигается, то она обязательно будет стационарной, однако если (·) М явл. стационарной, то в этой точке не обезательно достигается экстремум. Поэтому должны быть достаточно сформулированы условия сущ. экстремума. А=fxx''; B=fxy''; C=fyy''; Δ=AC-B².
Теорема 2 (достаточный условия экстремума локального). Пусть функция f(x,y) имеет непрерывные частные производные, до 3 порядка включительно в некоторый области содержащие стационарную точку М, тогда если:
1) Δ>0, то (·) М (x0,y0) явл. (·) экстремума для данной функции, причем А<0, (·)максимума и А>0 (·)минимума.
2) Δ<0, то (·) М (x0,y0) экстремума нет.
3) Δ=0, то экстремум может быть, а может и не быть, требуются дополнительные исследования.
Пр. Найти экстремум двух переменных. z=x²+xy+y²-3x-6y
1) ðz/ðx=2x+y-3=0; y=-2x+3; y=-2x+3; x=0;
dz/dy=x+2y-6=0; x+2*(-2x+3)-6=0; -3x=0; y=3; (·) M
2) ð²z/ðz²=2; A=2; ð²z/ðxðy=1; B=1; ð²z/ðy²=2; C=2;
|AC-B²|=|AB; BC|=2*2-1²=3. Если Δ>0, то в (·) М, есть экстремум. Т.к. А=2>0, то в (·) М1 – минимум.
3) z min (M1)=0²+0*3+3²-3*0-6*3=-9;
5.Наименьшее и наибольшее значения функции двух переменных в замкнутой области.
Пусть z= f(x, y) определены в замкнутой области Д с границей Г, дифференцируема во всех внутренних точках, тогда сущ. точки Р1 (x1, x1) (·)P2(x2, x2) в которых функция z прим. наибольшее и наименьшее значение (глобальный экстремум). (·) Р1 и Р2 или среди стационарных точек в нутрии области Д или среди точек принадлежащие границе. Сравнивая значения функции z в этих точках, и выбираем самое большое (наибольшее) и самое маленькое (наименьшее). Пр. найти наибольшее и наименьшее значение f. Z=3x+y-xy, в области Д: y=x; y=4;x=0.
1.
Начертить область Д.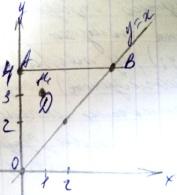 
2. Находим стационарные точки. ðz/ðx=3-y=0; y=3; ðz/ðy=1-x=0; x=1;
Найдём границы области ОА: x=0→ОА/z=y; z'=1≠0.
Исследуем граничные точки.
Границе АВ: y=4→AB; z=3x+4-4x=-x+4; z'=(-x+4)'=-1≠0;
Границе OВ: y=x; z=3x+x –x*x=-x²+4x; z'=-2x+4; z'=0→ -2x+4=0; x=2; y=2.
z min=z(0)=0, z min=z(B)=0; z max=z(A)=4; z max=z(M2)=4; (·)M2(2, 2).
6.Двойной интеграл. Основные понятия. Геометрический смысл двойного интеграла.
Двойной
интеграл. Пусть функция z=
f(x,
y)
не отрицательная, не непрерывная, в
замкнутой ограниченной областью,
уравнение z
= f(x,
y)
в пространстве определяется некоторую
поверхность F,
проекции которой на плоскость х, оу
совпадает с областью Д. Тело ограниченное
поверхностью, F
с низу областью Д и вертикальной
поверхность, в вдоль границы поверхности
Д наз. криволинейный
цилиндр.
Выполним следующие действия: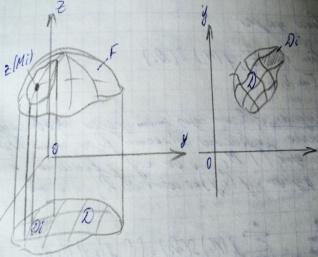 
1. Разобьём область Д гладкими дугами на n частей Дi. Обозначим S(Дi) – площадь области Дi.
2. Выберем в каждой частной области Дi произвольную (·)Mi (xi, yi) и вычислим значение функции z в выбранных (·). Z (Mi) и составим сумму которая наз. интегральной суммой. Vn=f(M1)*S (Д1)+f(M2)*S (Д2)+…+f (Mn)*S (Дn) = Σn i=1f (Mi)*S (Дi). Каждое слагаемое f (Mi)*S (Дi) можно представить геометрически как объём малого цилиндра. Основание которого Дi, а высота f (Mi). Сумм Vn – есть сумма элементарных цилиндров. При увеличении количества Дi, то есть при n→∞, Vn→объёму криволинейного цилиндра. Расм. lim n→∞ Σn i=1f (Mi)*S (Дi).
Опр.: Если сущ. этот предел независящий от способа разбиение области Д на часть Д и от выбора (·)Mi, то он наз.двойным интегралом от функции f(x, y) по области Д, то есть: lim n→∞ Σn i=1f (Mi)*S (Дi) = ∫∫д f(x, y)dxdy (1). Область д – наз. областью интегрирования, x, y – переменные интегрирования. dxdy=S(Дi) – элемент площади.
Для какой функции сущ. двойной интеграл?
Теорема: Если функция z= f(x, y) – непрерывна в замкнутой области Д, но она интегрируема в этой области.
Геометрический смысл: Объём цилиндра ограниченное сверху z = f(x, y), снизу замкнутой областью, Д є x0y, с боков цилиндрический поверхность (криволинейный цилиндр). Произведём действие записанные в предыдущем пункте. Объём цилиндра Vi=f (Mi)*S (Дi).Объём криволинейной цилиндра Vкр.ц.= Σn i=1Vi – это равенство тем точнее, тем что чем меньше Дi, тем больше n. Vкр.ц.= lim n→∞ Σn i=1f (Mi)*S (Дi)= ∫∫д f(x, y)dxdy (2).
Вывод: величина двойного интеграла от неотрицательной функции = объёму цилиндрического тела.