28.Знакопеременные и знакочередующиеся ряды. Признак Лейбница. Свойства абсолютно и условно сходящихся рядов.

Ряд вида: (1)

Остатком ряда (1) называется сумма: (2)

Теорема (Признак Лейбница) – дан знакочередующий ряд (1), тогда если:

1.Члены ряда убываю по абсолютному значению начиная с некоторой последовательности: (3)

2.Предел

То ряд (1) сходится и его сумма не превосходит 1-ого члена ряда 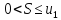- остаток ряда удовлетворяет неравенство.

Ряд удовлетворяющий теореме Лейбница называется рядом Лейбница. Неравенство дает оценку остатка ряда Лейбница.

Свойства абсолютно и условно сходящихся рядов: Пусть даны два ряда и , они сходятся абсолютно к ;, тогда:

1)Ряд ;

2)Ряд , (где α – действительное число);

3)Пусть ряда –сходится условно, тогда оба ряда полученных только из положительных и только из отрицательных членов этого ряда расходятся;

4)Если ряд –сходится абсолютно и его сумма равна A, то при перестановке его членов ряд остается сходящимися и его сумма не меняется;

5)Если ряд –сходится условно, то наперед заданного числа C, существует перестановка членов ряда, такая, что сумма полученного ряда равна C.

29.Функциональные ряды. Область сходимости. Сходимость ряда .

Ряд 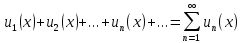(1)

Ряд (1) называется функциональным, т.к. его члены являются функциями от x. Давая x определить числовые значения мы получим различные числовые ряды, которые могут сходится или расходится.

Определение: Совокупность тех значений x, при которых функциональный ряд сходится, называется областью сходимости этого ряда.

Сумма ряда обозначается S(x) и она является функцией от (x).

–это ряд геометрической прогрессии, со знаменателем q = x. Ряд сходится , т.е.или - область сходимости. ,.

30.Степенные ряды . Теорема Абеля. Интервал и радиус сходимости степенного ряда.

Среди функций рядов особую роль играют ряды, членами которых являются степенные функции.

Определение: Степенным рядом называется функция ряда вида: 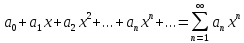(1)

- постоянные числа, называются коэффициенты ряда.

- действительная переменная.

Рассмотрим ряд: (2)

Ряд (2) – степенной ряд со степенями , – некоторое число. Ряд (2) сводится к ряду (1) заменой: . Поэтому будем рассматривать только ряд (1). Выясним вопрос о сходимости ряда (1).

Теорема Абеля:

1.Если степенной ряд (1) сходится, при некотором значении , то абсолютно сходится при всяком значенииx, для которого ;

2.Если степенной ряд (1) расходится, при некотором значении , то он расходится при всякомx удовлетворяющем неравенству ;

Поясним теоремы:

1.Если ряд (1) сходится в точке 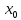, то он абсолютно сходится в интервале (;) с центром в точкеO;

2.Если ряд расходится в точке , то он расходится в интервалах . Отметим это на числовой прямой:

Вывод: Область сходимости степенного ряда (1) является интервал конечный и бесконечный с центром в точке O или единственная точка O.

Положим , тогда интервал сходимости будет(-R,R). Число R называется радиусом сходимости степенного ряда, т.е. это такое число, что при всех степенной сходится абсолютно, а при всехрасходится.

Если степенной ряд сходится лишь в одной точке , то считаем. Если ряд сходится при всех, то считаем. На концах интервала, т.е. присходимость проверяется отдельно.

Для нахождения радиуса сходимости степенного ряда (1) можно использовать признак Даламбера или признак Коши. Допустим, что существует предел: . Тогда по признаку Даламбера имеем: , тогда ряд сходимости для всех . Таким образом, радиус сходимости можно найти: (3)

Аналогично рассуждаем, если применить признак Коши, тогда радиус: (4)

Замечание: Интервал сходимости степенного ряда (2) находят из неравенства и он имеет вид.