1.Функция двух переменных. Определение. Геометрическое изображение.
Опр.
Пусть Д некоторое множество (·) М (x,
y),
є плоскости. Правило f
ставящие в соответствие (·) (x,
y),
определённое единственное число z
у множество действительных наз. функцией
двух переменных
z=f(x,
y)
– функция двух переменных, где (x,
y)
– независимая переменная, z
– функция. Множество Д – наз. Областью
определения функции множество є
состоящая из чисел {z
є |B, для которых z=f(x,
y)}
наз. областью значений. Пр.
Правило f:
(x,
y)―>
(x²-y²)
ставящие
в соответствие каждая пара (x²-y²)
определяет
функцию двух переменных z=x²-y².
Пр.
Найти область определение функции двух
переменных и изобразить на плоскость
z
= 1/√1-x²-y²
Д (z):
пару чисел {(x,
y):1-x²-y²>0}
1- x²-y²>0;
1> x²+y²
построим границу области 1= x²+y²
- окружность цент О, радиус 1. (·)(0,0)→
1,0²+0² - верно. Область определения явл.
(·)лежащей в нутрии границы.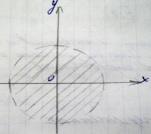 
Граница
не входит в область определения.
Аналогично определяется количество
двух и более переменных. Двух переменных
функцию можно изобразить графически.
Для этого в (x,
y)
є Д вычисляется значение z=f(x,
y).
Тройка чисел (x,
y,z)
определяет в системе координат О x,y,z
некоторую точку Р совокупность точек
представляет собой некоторую поверхность
которая и явл. графиком функции z=f(x,
y).
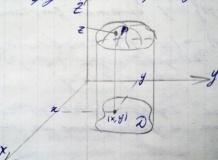
Предел
функции в точке.
Для функции двух переменных вводиться
понятие предела функции, непрерывность
аналогично случаю функции одной
переменной. Введём понятие окрестность
точек. Опр.
Множество всех (·)М (x,
y),
плоскости координаты которых удовлетворяет
неравенству √(x-x0)²+(y-y0)²<δ
(дельта) наз. дельта
окрестностью точки М0
(x0,
y0).
Другими
словами
δ
окрестности (·) М0
(x0,
y0)
это внутренние (·) круга с центром М0
и радиусам δ. Опр.
Пусть функция z=f(x,
y)
определена в некоторой окрестности (·)
М0
с координатами (x0,
y0)
кроме самой (·) М0.
Числа А – наз. пределом функции z=f(x,y), в(·) М0 то есть при х→ x0, y→ y0
Если для любого множества ε сущ. δ>0, что для всех (·) х, не х≠x0, y≠y0 → неравенство | f(x, y)-А|<ε lim f(x, y)=A(х→x0, y→y0
Геометрический смысл: каково бы ни было число ε надеться δ окрестность в (·)М0, что во всех (·)≠0, аппликаты соответствующих (·)поверхности z=f(x, y), отличаются от числа А, по модулю< чем ε (ипсилон). Если предел сущ. то он не зависит от пути по которому (·)М→ М0.
Пр. Найти предел функции. lim x→0 y→0x²-y²/x²+y²=0/0
Пусть (·) М(x, y) приближается к (·)О (0,0) по прямой y=kx
lim x→0 y→0x²-y²/x²+y²= lim x→0 y→0 x²-kx²/ x²+kx²= lim x→0 y→0 x²(1-k²)/ x²(1-k²)=1-k²/1+k². Вывод: функция z=x²-y²/x²+y² в (·) О (0,0) придела не имеет, так как при различных значении k разные.
Пр. lim x→0 y→0x²+y²/(√x²+y²+1)-1=[0/0]== lim x→0 y→0 (x²+y²)((√x²+y²+1)+1)/((√x²+y²+1)-1) ²)/
((√x²+y²+1)+1) = lim x→0 y→0 (x²+y²)((√x²+y²+1)+1)/x²+y²+1-1= lim x→0 y→0 (√x²+y²+1)+1)=2
Предел функции двух переменных обладает свойствами аналогичными свойства предела функции одной переменной, то есть:
1. lim (f+g) = lim f+ lim g;
2. lim f*g = lim f*lim g
3. lim f/g = lim f/lim g, lim g≠0