
Начертательная геометрия
.pdf
|
|
|
|
|
|
|
|
|
|
|
Прямая общего положения |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2.1. Прямая общего положения |
|
|
|
|
|
|
|
|
||||||||
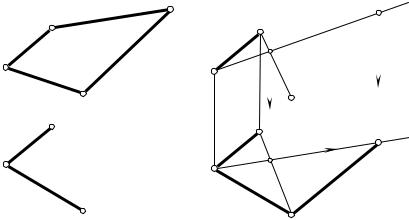
Прямая общего положения и её проекции |
|
Следы прямой |
|
|
Деление отрезка в заданном |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отношении (например, 1:3) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фронтальный |
V" |
|
|
|
|
|
N" |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
след |
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
B" |
|
|
|
|
|
B" |
|
|
|
|
D" |
|
|
|
|
|
|
|
У |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
C" |
|
|
|
|
|
|
|
|
|
C" |
|
|
|
|
|
|
|
|
|
|
|
E" |
||
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A" |
|
|
|
|
С |
|
|
|
|
|
|
|
C" |
|
|
|
|
|
|
M" |
|||||
|
|
|
|
|
|
|
|
A" |
|
|
x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
H" |
|
|
|
V' |
|
|
|
|
||||
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
M' |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
E' |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A' |
|
|
C' |
|
|
|
|
A' |
|
|
|
|
|
|
|
|
|
соединить |
|
|
N' |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||
|
|
H |
|
|
|
|
|
|
B' |
|
|
C' |
|
|
H' |
C' |
|
|
|
|
|
|
1 |
Т |
||
Не параллельна плоскостям проекций H, |
B' |
горизонтальный след |
|
|
|
|
|
произвольное |
||||||||||||||||||
V и W. Точка С лежит на прямой AB. |
|
|
|
прямой - |
точка пе- |
|
|
M" |
|
|
||||||||||||||||
|
|
|
ресечения |
прямой |
|
с |
|
|
направление |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фронтальной |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г о р и з о н т а л ь н о й |
|
|
|
|||||||||
|
|
|
|
а. |
|
|
|
|
|
б. |
|
|
|
Нпроекции M"N" |
||||||||||||
|
|
|
|
|
|
|
|
|
|
плоскостью |
|
|
|
H |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отрезка, т.е. |
||||||||||
|
|
|
à |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
á |
|
|
|
|
|
â |
|
|
|
|
ã |
|
N'M"=N"M" |
|||
|
|
|
|
|
|
|
|
|
Рис. 2.1 |
|
|
|
|
|
. |
2.2 |
|
|
Б |
2.3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. |
|
|
||||||
|
Теорема о принадлежности точки |
|
|
|
: если точка принадлежит пря- |
|||||||||||||||||||||
мой, то на чертеже одноимённые п оекц |
проекций |
|
|
|
|
|
||||||||||||||||||||
точки лежат на одноимённых про- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
à, á |
è å |
|
|
Рис |
|
|
|
|
|
|
|
|
||||
екциях прямой (см. рис. 2.1а, |
б; 2.4б). |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
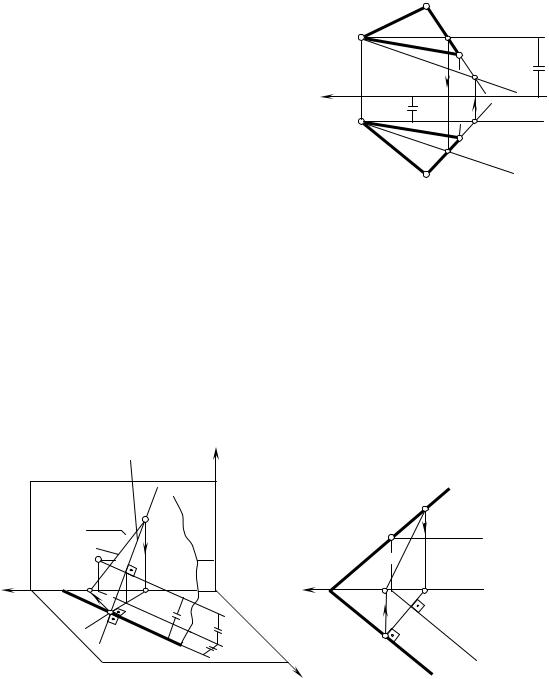
Определение натуральной величины |
прямой |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
трезка способом прямоугольного треугольника |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
на чертеже |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
||
C'C"D" - повернуть |
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и совместить с плос- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
костью V |
|
|
|
|
|
|
фронтальный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
след |
|
|
|
|
|
Нат. вел. CD |
|
|
|
V |
D" |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
V |
|
|
|
|
|
|
Dи |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
||
|
|
|
|
|
|
|
|
. C |
D"(V) |
|
|
|
|
C0" |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
ел |
|
|
|
|
|
|
|
|
|
|
|
K" |
|
|
|
|
|||
|
|
|
|
|
|
.в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
||
|
|
|
а |
зV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
C0" |
Н |
|
C'D"D' - повернуть |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
z |
|
и совместить с плос- |
|
C" |
|
|
|
|
|
C'K' и C"K" - |
|||||||
|
|
y |
|
|
|
|
V |
|
|
костью H |
|
|
|
x |
|
|
|
|
|
|
проекции отрезка |
|||||
|
x |
о H |
D' |
z |
|
|
|
|
|
|
|
|
|
|
D' |
длиной 20 мм |
||||||||||
|
|
C" |
|
y |
|
|
|
|
|
|
|
|
|
|
y |
|
|
K' |
|
|
|
|
|
|||
|
пC'(H) |
|
H |
|
|
|
|
|
|
|
|
|
|
H |
|
z |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
K0 |
|
|
|
|
||||||||||
|
Нат.вел. |
|
|
|
|
|
|
|
C' |
|
|
|
D0 |
|
|
|
||||||||||
|
C |
D0" |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
е |
|
|
|
|
|
|
H |
|
D |
|
|
|
|
|
20 |
мм |
|
Нат. вел. CD |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
горизонтальный |
|
|
|
|
|
|
|
- угол наклона отрезка к плоскости проекций V |
||||||||||||||||||
Р |
|
|
|
след |
|
|
|
|
|
|
|
|
V |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
H |
- угол наклона отрезка к плоскости проекций H |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
ä |
|
|
|
|
|
|
|
|
|
|
|
|
å |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.18 |
|
|
|
|
|
|
|
|
|
Ëèñò 2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
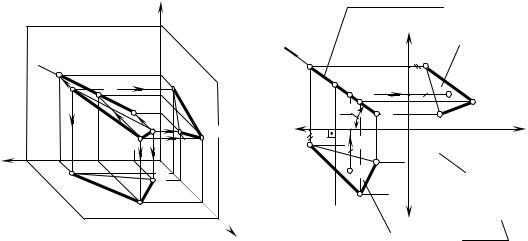
Прямые частного положения |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2.2 Прямые частного положения |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Горизонтальная прямая уровня: //HH |
|
|
|
|
Фронтальная прямая уровня: //VV |
||||||||||||||||||||||
|
V |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
Нат. |
вел. |
|
z |
|
|
|
||
|
|
E" |
|
F" |
|
|
|
E" |
|
|
F" |
|
|
|
E"' |
|
|
|
V |
|
|
|
B" |
|
|
B'" |
||||
|
|
E |
|
|
|
|
|
|
yE |
F"' |
|
|
B" |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A" |
|
|
|
A" |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
y |
|
|
B |
|
|
|
|
yA |
A"' |
||||
x |
|
|
|
|
|
O |
x |
|
|
|
|
O |
|
|
|
|
|
A |
|
|
|
|
|
|
||||||
|
|
E' |
|
|
|
|
|
|
|
|
|
x |
|
|
|
O |
x |
|
|
|
O |
|
y |
|||||||
|
|
|
|
|
|
yE |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
H |
|
|
|
E' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yA |
|
|
|
|
|
|
|
|
|
|
|
|
|
F' |
|
|
|
|
|
|
|
|
|
|
|
|
A' |
|
B' |
A' |
|
|
B' |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||||
|
|
EF |
|
|
|
|
Нат. вел. |
|
|
|
|
|
|
|
y |
|
|
H |
|
|
|
V |
|
|
||||||
|
|
H |
|
|
|
|
F' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
FE // |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB // V |
|
||||||||||||
|
|
|
|
а. |
à |
|
|
|
|
|
|
áб. |
|
|
|
|
|
а. â |
|
|
|
|
ã б. |
|
|
|
||||
|
|
|
|
|
|
|
Рис. 2.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.6 |
|
|
Т |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Профильная прямая уровня: WW |
|
|
|
Горизонтально-проецирующая прямая: |
H |
|||||||||||||||||||||||
|
|
|
|
|
H |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
// |
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
||||
|
|
|
|
z |
|
|
|
C" |
|
z |
C'" |
|
|
|
|
|
|
z |
|
Б |
|
|
|
|
|
|
||||
|
|
C" |
|
|
|
|
|
|
|
Н.в. |
|
E" |
|
|
|
E" |
|
z |
y |
E"' |
|
|||||||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
C'" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
Нат. вел. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
yD |
D'" |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
D" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E"' |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
D" |
|
|
|
|
|
F" |
|
|
|
|
F" |
|
|
|
F"'y |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||||||||
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
й |
x |
|
|
O |
|
|||||||
|
|
|
O |
|
|
D" |
|
|
O |
|
|
|
|
|
|
F |
O |
F"' |
|
|
|
|
|
|
|
|||||
|
|
|
|
D |
|
|
C' |
|
|
|
|
|
|
|
|
|
|
E' |
F' |
|
|
|
y |
|
|
|
y |
|
||
|
|
C' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E' |
(F') |
|
|
|
|
||||||||
|
|
|
|
|
|
yD |
|
|
|
|
|
|
|
|
и |
|
|
|
y |
|
|
|
||||||||
|
|
|
D' |
|
|
y |
D' |
|
y |
|
|
|
y |
|
|
y |
|
|
|
|
|
|
|
|||||||
CD W |
|
|
|
|
|
|
|
|
EF H |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
CD // W |
|
|
|
|
|
|
|
|
|
|
|
|
|
EF |
H |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
а. ä |
|
|
|
|
|
б. |
|
|
р |
|
|
|
æа. Рис. 2.8 |
|
|
|
б. |
|
|
|||||||
|
|
|
|
|
Р с. |
2.7 |
|
|
å |
|
|
|
|
|
|
|
|
|
ç |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
т |
V |
|
|
|
Профильно-проецирующая прямая: W |
|||||||||||||||
|
|
Фронтально-проец рующая прямая: |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
z |
|
|
|
и |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
z |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
A" |
B" |
|
|
з |
|
z |
y |
B"' |
|
A"' |
|
|
|
C" |
|
D" |
|
|
|
С |
D |
|
C"' |
(D'") |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
А" |
(B") |
|
|
|
|
|
|
|
|
C"' |
(D'") |
|
|
|||||||||||
|
|
|
|
|
|
B"' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
||||
|
|
|
B |
оA |
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
D |
|
|
|
|
|
|
y |
|
|||
x |
|
|
|
x |
|
|
O |
|
|
|
|
|
x |
|
|
|
O |
|
x |
|
|
O |
|
|
||||||
|
|
|
B' |
O |
|
|
A"' |
y |
|
|
|
|
|
|
|
|
|
|
C' |
|
y |
|
y |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
D' |
|
|
|
|
|
|
|
|
|||
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
е |
A' |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
C' |
D' |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CD W |
|
|
|
|
|
|
|
|
||||||
|
|
Нат.вел. |
A' |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
AB VV |
|
|
|
|
|
|
|
|
|
|
|
|
CD |
W |
|
|
|
|
|
|
|
|
|
|||||||
Р |
|
|
è |
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
ë |
|
|
|
|
ì |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.19 |
|
|
|
|
|
|
|
|
|
Ëèñò 3 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
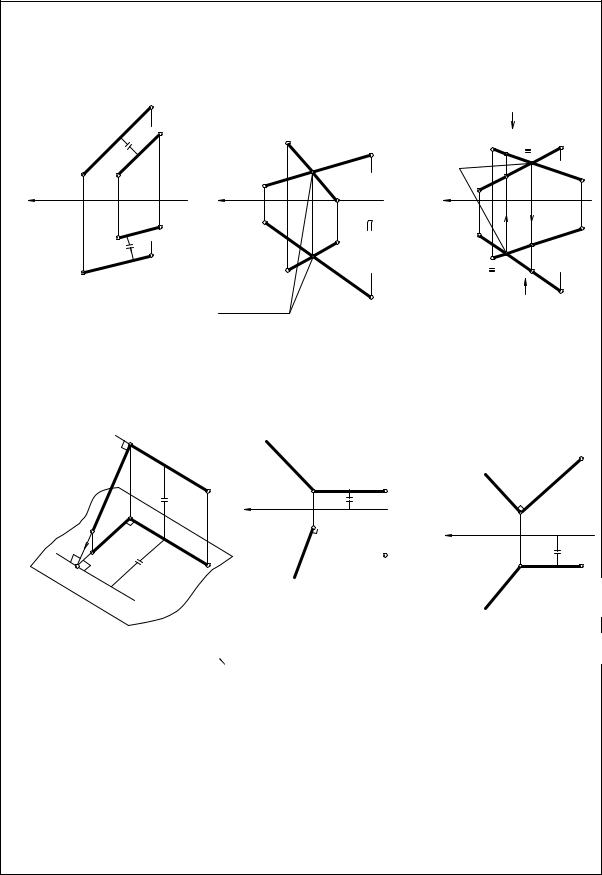
2.3 Взаимное расположение прямых |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Взаимное положение прямых |
|
|
|
|
|
|
|
||||||
|
|
|
Параллельные прямые |
|
|
Пересекающиеся прямые |
|
Скрещивающиеся прямые |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
B" |
|
|
|
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
D" |
|
|
|
|
E" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D" |
|
|
M" |
|
|
|
F" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1" 3" |
(4") |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O" |
|
|
|
|
|
|
|||||
|
|
|
|
|
A" |
|
C" |
|
|
|
|
|
|
|
|
Наложение |
|
|
|
|
N" |
|||||
|
|
|
|
|
|
|
|
|
C" |
|
|
|
|
проекций |
E" |
2" |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
F" |
|
прямых x |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
AB |
CD |
|
|
|
D' |
|
|
|
|
C' |
|
|
CD |
EF |
|
|
|
|
|
|
|
|
||||
// CD |
|
|
|
|
|
|
|
|
|
|
|
|
E' |
|
4' |
|
|
N' |
||||||||
|
|
|
|
|
|
|
|
|
C' |
|
|
|
|
|
|
|
F' |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O' |
|
|
|
|
M' |
|
|
У |
||||
|
|
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
3' |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1' |
(2') |
|
|
|
||
|
|
|
|
|
A' |
|
|
|
|
|
|
|
E' |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D' |
|
|
|
V |
|
|
F' |
|
|||
Проекции прямых параллельны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Т |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Общая точка |
|
|
|
|
|
1-2 и 3-4 - конкурирующие точки |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(каждая пара точек лежит на |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
пересечения |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
одном проецирующем луче) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Рис. 2.11 |
|
|
|
|
|
á |
|
|
|
|
|
Н |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
à |
|
|
|
|
|
Рис. 2.12 |
|
|
Б |
Рис. 2.13 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Теорема о проекции прямого угла |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2.4 Теорема о проекции прямого угла |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
n"(дана) |
по условию |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по услов ю |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
||
|
ABC |
90 |
|
|
|
|
|
|
|
|
|
|
|
n |
BC |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
С |
|
|
|
B" |
|
n BC C" |
|
|
k"(построена) |
|
|
E" |
||||||||
ABC=90°= ° |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
и |
|
|
k"-? |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
B' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D" |
|
|
|
|||
|
|
|
|
|
|
|
A |
|
|
|
|
|
B' |
|
|
|
|
x |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
C' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A' |
|
|
|
|
n'-? |
|
|
|
|
|
|
D' |
|
E' |
||||
|
|
|
|
|
|
|
|
|
|
C' |
|
оn'(построена) |
|
|
|
|
|
|||||||||
|
|
|
|
|
K' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
m |
|
т |
|
|
|
|
|
|
|
|
|
по условию |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по условию |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k DE |
|||||
|
m |
|
|
H |
|
|
|
|
|
|
|
|
k'(дана) |
|
k |
DE |
||||||||||
|
m |
|
BK' |
|
|
|
m B'K', иа B'K' B'С', |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Если m BK', |
Так как BC H, то n' B'С' |
|
Так как DE V, |
то |
k" D"E" |
|||||||||||||||||||||
Òàê êàê BC // H, òî n' |
B'C' |
|
Òàê êàê DE//V, òî k" |
D"E" |
|
|||||||||||||||||||||
Åñëè |
m |
BK', òî m |
B'K', à B'K' |
B'C', |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
т.е. |
|
|
K'B'С |
|
. Если BC H, |
а АB H, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
òî åñòü |
K'B'C''=90°90°. Åñëè BC // H, à AB // H, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
то |
|
|
A'B'С'=90° |
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
òî |
|
A |
'B'C' |
90 |
°. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Рис. 2.14а |
|
|
|
|
Рис. |
2.14б |
|
|
|
|
å |
|
|
|
||||
|
|
|
|
|
|
|
|
|
ã |
|
|
|
|
|
ä |
|
|
|
|
|
|
2.14в |
||||
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. |
||||||
|
|
пТ орема о проекции прямого угла: если одна сторона прямого угла па- |
||||||||||||||||||||||||
р лл льна плоскости проекций (а вторая не параллельна и не перпендикуляр- |
||||||||||||||||||||||||||
ена этой плоскости), то на эту плоскость проекций прямой угол проецируется |
||||||||||||||||||||||||||
в виде прямого угла. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Р |
|
|
|
|
Знак перпендикулярности элементов: . |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.20 |
|
|
|
|
|
|
|
Ëèñò 4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лекция 3
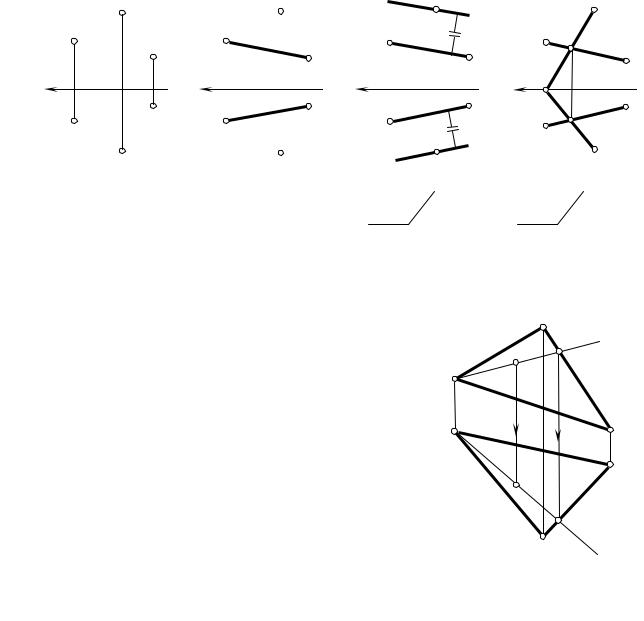
ПРОЕКЦИИ ПЛОСКОСТИ. ЗАДАНИЕ ПЛОСКОСТИ НА ЧЕРТЕЖЕ. СЛЕДЫ ПЛОСКОСТИ. ПОЛОЖЕНИЕ ПЛОСКОСТИ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
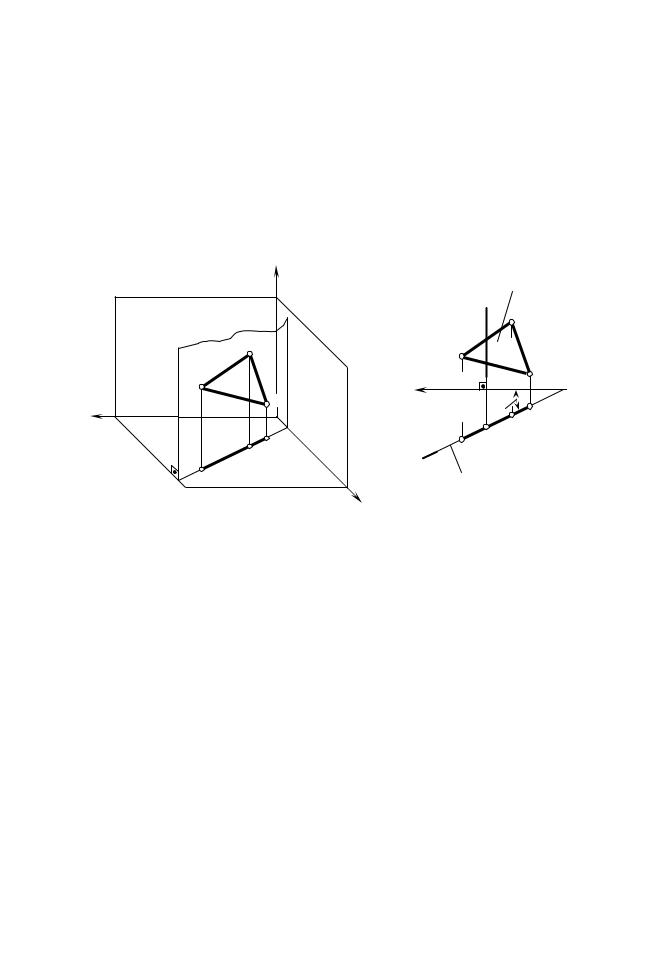
Плоскость. Способы задания плоскости на чертеже Из геометрии известно, что плоскость в пространстве определяется
–проекциями трех точек, не лежащих на одной прямой (рис. 3.1,Уа);
–проекциями прямой и точки, взятой вне прямой (рис. 3.1,Тб);
–проекциями двух параллельных прямых (рис. 3.1, в);
–проекциями двух пересекающихся прямых (рис. 3.1,Нг);
–проекциями замкнутого отсека любой формы – треугольника, четырехугольника и т. д. (рис. 3.2). Бтремя точками, не лежащими на одной прямой. В соответствии с этим начертеже C"
x |
|
|
x |
|
|
x |
|
й C' |
x |
|
|
||
A' |
|
C' |
A' |
|
C' |
|
A' |
D"≡D' |
E' |
C' |
|||
|
|
|
|
|
|
|
|
||||||
|
B' |
|
|
B' |
|
иB' |
|
|
A' |
|
βW |
||
|
|
|
β(AC, B) р |
m' |
|
|
|
|
|
||||
α(ABC) |
|
γ(AC // m) |
|
δ(AC ∩ BD) |
|||||||||
|
|
|
|
о |
Знак |
|
|
Знак |
|
|
|||
|
|
|
|
|
|
|
|
пересечения |
|
||||
|
|
|
тб |
|
параллельности |
|
|
|
|||||
а |
|
|
|
|
|
в |
|
|
|
г |
|
||
|
|
|
и |
|
Рис. 3.1 |
|
|
|
точка K m α |
|
|||
|
|
|
|
|
|
|
|
|
|
||||
Точка |
зпрямая в плоскости |
|
|
B" |
|
m" |
|||||||
Из ге метрии известны теоремы о принад- |
|
|
K" |
|
|||||||||
|
|
1" |
|
||||||||||
|
точкипрямой линии плоскости: |
|
A" |
|
|
||||||||
|
|
|
|
|
|
||||||||
1-я т орема: точка принадлежит плоско- |
|
|
|
|
|
||||||||
сти, псли она принадлежит прямой линии, ле- |
A' |
|
|
|
C" |
||||||||
жащ й в этой плоскости. |
|
|
|
|
|
|
|
|
|||||
лежности |
|
|
|
|
|
|
|
|
|
|
|
|
|
2-я теорема: прямая линия принадлежит |
|
|
|
|
C' |
||||||||
плоскости, если она проходит через две точки, |
|
|
K' |
|
|||||||||
|
|
|
|
||||||||||
Рлежащие в этой плоскости. |
|
|
|
|
|
|
|
|
|
|
|||
На рис. 3.2 показано применение этих тео- |
|
|
|
1' |
|
||||||||
рем для построения горизонтальной проекции |
|
|
B' |
|
m' |
||||||||
точки К(K", K'-?), лежащей в плоскости, задан- |
|
|
|
||||||||||
|
|
|
|
|
|||||||||
ной треугольником ABC. Для решения этой |
|
|
Рис. 3.2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
задачи требуется выполнить следующий графический алгоритм (графические действия):
1-е действие. Провести в заданной плоскости фронтальную проекцию вспомогательной прямой m(m") через две точки этой плоскости – например, через точку А(A") и заданную фронтальную проекцию точки K(K"); эта прямая пересекает сторону ВС треугольника в точке 1(1",1').
2-е действие. Провести горизонтальную проекцию вспомогательной прямой m(m') через горизонтальные проекции точек А(A') и 1(1').
3-е действие. Построить по линии связи искомую горизонтальную проекцию точки K(K') на горизонтальной проекции вспомогательной пря-
мой m(m'). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
||||||
|
На рис. 3.3, а, б показано решение задачи, где требуется достроитьУго- |
|||||||||||||||||||||
ризонтальную проекцию четырехугольника ABCD(A",B",C",D"; A',B',C',D'-?, |
||||||||||||||||||||||
C'-?). Для решения задачи выполнены следующие графические построенияТ: |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
– проведены проекции диагонали AC(A"C", A'C'); |
|
|
|
|
|||||||||||||||||
|
– проведена фронтальная проекция диагонали BD(B"D"); |
|
|
|||||||||||||||||||
|
– определены проекции вспомогательной точки 1(1"1'), принадлежащей |
|||||||||||||||||||||
диагоналям AC и BD; |
|
|
|
|
|
|
|
й |
|
– проведена че- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Условие |
|
|
|
|
|
|
|
|
Решен е |
|
|
рез точки B' и 1' го- |
||||||
|
|
|
|
|
|
|
|
|
D" |
|
|
|
|
|
и |
|
d" |
ризонтальная проек- |
||||
|
A" |
|
|
|
|
|
|
|
|
|
A" |
|
|
|
D" |
ция диагонали d(d'), |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1" |
|
|
на которой должна |
|||||
B" |
|
|
|
|
|
|
|
|
B" |
|
|
|
|
р |
|
|
|
лежать |
проекция |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
C" |
|
|
|
|
|
|
|
|
|
вершины D(D'); |
|||||||
|
|
|
|
|
|
и |
|
|
|
|
|
C" |
|
|
|
|
– построена по |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
A' |
|
|
|
|
|
A' |
|
|
|
|
|
d' |
линии |
связи |
гори- |
||||||
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|||||||
B' |
|
|
|
|
|
з |
т |
|
|
|
|
|
|
D' |
зонтальная |
проек- |
||||||
|
|
|
|
|
о |
|
B' |
|
|
|
1' |
|
|
|
|
ция D' вершины D |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по ее принадлежно- |
||||||
|
|
|
|
C' |
|
|
|
|
|
|
|
|
|
C' |
|
|
|
|
сти прямой d(d'); |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– достроена го- |
||||||
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|||
е |
|
|
|
|
|
Рис. 3.3 |
|
|
|
|
|
|
|
ризонтальная проек- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ция A'B'C'D' |
четы- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рехугольника ABCD. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Прямые особого положения в плоскости . Гори - |
|||||||||||||||||||||
зонталь h и |
ф р о н т а л ь f |
п л о с к о с т и |
|
|
|
|
||||||||||||||||
Прямые линии, лежащие в плоскости и параллельные фронтальной плоскости проекций V, называются фронталями – f(f",f').
Прямые линии, лежащие в плоскости и параллельные горизонтальной плоскости проекций H, называются горизонталями – h(h",h').
На рис. 3.4 показано построение в плоскости треугольника DEF проекций фронтали и горизонтали.
34
Поскольку фронталь плоскости f парал- |
Плоскость общего положения |
|
|||||||||||||||||
лельна фронтальной плоскости проекций V, |
|
|
E" |
|
|
||||||||||||||
построение ее проекций следует начинать |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||
с горизонтальной проекции фронтали f', ко- |
D" |
|
2" |
h" // x |
|||||||||||||||
торая должна быть на чертеже параллельна |
|
|
F" |
|
|
||||||||||||||
оси x. Фронтальная проекция фронтали f" |
x |
|
1" |
f" |
|
||||||||||||||
строится по ее принадлежности заданной |
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||
плоскости с помощью вспомогательной точ- |
D' |
|
|
f' // x |
|
||||||||||||||
ки 1(1',1"). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1' |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поскольку горизонталь плоскости h па- |
|
|
F' |
h' |
|
||||||||||||||
|
|
2' |
|
||||||||||||||||
раллельна |
горизонтальной |
|
плоскости |
про- |
|
|
E' |
У |
|||||||||||
екций H, |
построение ее проекций следует |
|
|
||||||||||||||||
|
Рис. 3.4 |
||||||||||||||||||
начинать с фронтальной проекции горизон- |
|
|
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||
тали h", которая должна быть на чертеже параллельна оси x. ГоризонтальТ |
- |
||||||||||||||||||
ная проекция горизонтали h' строится по ее принадлежности заданной |
|||||||||||||||||||
плоскости с помощью вспомогательной точки 2(2',2"). |
Н |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Прямые линии, лежащие в плоскости и перпендикулярные горизонтали |
|||||||||||||||||||
этой плоскости, называются линиями наибольшего наклона (ската) плоско- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
сти. Они определяют угол наклона плоскости к плоскости проекций H. |
|
||||||||||||||||||
На рис. 3.5, а изображена линия на большего ската m в плоскости α, |
|||||||||||||||||||
а на рис. 3.5, б – построение ее |
|
|
|
|
й на чертеже этой плоскости, за- |
||||||||||||||
данной следами. |
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|||||
Линия наибольшего наклона |
|
|
|
|
z |
|
|
|
|
|
|
||||||||
(ската) плоскости α |
|
|
|
|
проекц |
|
|
|
|
|
|
||||||||
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
о |
|
|
|
|
2" |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
αV≡αV" |
2" |
|
|
|
|
|
αV" |
h" |
|
|
|||||||
|
|
m" |
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
m |
|
|
|
h" |
|
|
|
|
|
m" |
|
|
|
||
x |
|
1" |
и |
|
h |
|
|
|
|
x |
2" |
2' |
αV'≡αH" |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1' |
|
2' |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
зm' |
|
|
|
h' |
|
|
|
|
|
|
|
m' |
|
|
|
||
|
о |
|
|
|
|
|
|
|
|
|
|
|
1' |
|
h' |
|
|
||
|
H |
αH≡αH' |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
y |
|
αH' |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
п |
|
|
|
а |
|
|
|
|
|
Рис. 3.5 |
|
б |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Понятие о следах плоскости |
|
|
|
|
|
||||||||||||||
Следами плоскости называются линии, по которым плоскость пересе- |
|||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кается с плоскостями проекций: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
–горизонтальный след – линия пересечения плоскости с плоскостью проекций H;
–фронтальный след – линия пересечения плоскости с плоскостью проекций V;
35
|
– профильный след – линия пересечения плоскости с плоскостью про- |
|||||||||||||||||
екций W. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!!! На чертежах вырожденные в прямые линии проекции |
|||||||||||||||||
плоскостей частного положения совпадают с соответствующими сле- |
||||||||||||||||||
дами этих плоскостей и их можно обозначать как следы (см. рис. 3.6, 3.7, |
||||||||||||||||||
3.8, 3.9, 3.10 и 3.11) этих плоскостей. |
|
|
|
|
|
|
|
|
||||||||||
|
Положение |
плоскости |
относительно |
плоскостей |
||||||||||||||
проекций. Плоскости общего положения и плоскости |
||||||||||||||||||
частного положения |
|
|
|
|
|
|
|
|
|
|||||||||
|
Относительно плоскостей проекций V, H и W плоскости в пространстве |
|||||||||||||||||
могут занимать семь различных положений – общее и шесть частных – |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
и имеют соответствующие названия и характерные признаки проекций на |
||||||||||||||||||
чертежах. Следовательно, по заданным проекциям плоскости можно пред- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
ставить ее положение в пространстве, то есть «прочитать» чертеж плоскости. |
||||||||||||||||||
|
Плоскость, не перпендикулярная ни одной из плоскостей проекций |
|||||||||||||||||
(см. рис. 3.1, 3.2, 3.3, 3.4, 3.5), называется плоскости общегоНположения. |
||||||||||||||||||
|
!!! Запомните характерные признаки плоскости общего положения на |
|||||||||||||||||
чертеже – ни одна ее проекция не вырождаетсяБ |
в линию, |
|||||||||||||||||
и каждая проекция искажает величину той формы, которой плоскость за- |
||||||||||||||||||
дана на чертеже. |
|
|
|
|
|
|
|
й |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Плоскости частного положен я, пе пендикулярные одной плоско- |
|||||||||||||||||
сти проекций, называются |
|
|
ующ |
плоскостями. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ми |
|
|
|
|
|||
|
Фронтально-проецирующая пл ск сть перпендикулярна фронтальной |
|||||||||||||||||
плоскости проекций V. На рис. 3.6 плоскость задана двумя перессекаю- |
||||||||||||||||||
щимися прямыми DE и EF; |
р |
|
|
|
|
|
|
|
||||||||||
г риз нталь плоскости h преобразуется здесь |
||||||||||||||||||
во фронтально-проецирующую прямую (h |
|
V). |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
проеци |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Фронтальнот-проецирующая плоскость |
|
|
|
|
|||||||||
|
|
|
|
|
|
иz |
|
|
Вырожденная проекция |
|
||||||||
|
|
|
|
з |
|
|
|
|
|
|
плоскости |
|
|
|||||
|
V |
|
|
|
|
|
βV |
|
|
|
|
z |
Искажённая |
|||||
|
βV |
D" |
|
|
|
|
|
|
|
|
|
D" |
|
|
|
D"' |
величина |
|
|
|
|
|
|
|
|
|
|
|
h" |
|
|
|
|||||
|
|
|
|
|
|
D"' |
|
|
|
|
|
|
|
|
|
|||
|
|
о |
|
|
|
|
|
K" |
|
yk |
|
|
||||||
|
|
D |
|
E" |
|
|
|
|
W |
|
|
|
|
|
E"' |
|||
|
|
|
|
|
F" |
|
|
|
|
E" |
|
|
|
|||||
|
п |
|
|
|
|
|
x |
|
φH |
F" |
|
F"' |
y |
|||||
|
|
|
|
F |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
E"' |
|
|
yk |
|
0 |
||||
x |
|
|
|
E |
F"' |
D' |
|
|
|
Знак пересечения |
||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
|
D' |
|
|
|
|
F' |
|
|
|
|
|
|
K' |
F' |
β(DE ∩ EF) V |
||
|
|
H |
|
|
E' |
|
|
|
|
|
h' E' |
|
y |
h V |
||||
|
|
|
|
|
|
y |
|
|
|
Точка K β |
||||||||
|
|
|
|
|
|
|
|
Искажённая |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Знак |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
величина |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
принадлежности |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
а |
|
|
Рис. 3.6 |
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!!! Запомните характерные признаки фронтально-проецирующей плос- |
|||||||||||||
кости на чертеже – ее фронтальная проекция представляет собой прямую |
||||||||||||||
(вырожденная проекция βV), наклоненную к оси проекций x, и определяет |
||||||||||||||
угол наклона плоскости к плоскости проекций H. Горизонтальная и про- |
||||||||||||||
фильная проекции плоскости представляют собой искаженную по вели- |
||||||||||||||
чине форму, которой эта плоскость задана на чертеже. |
|
|
|
|||||||||||
|
Горизонтально-проецирующая плоскость перпендикулярна горизон- |
|||||||||||||
тальной плоскости проекций H. На рис. 3.7 плоскость задана треугольни- |
||||||||||||||
ком ABC; фронталь плоскости f преобразуется в горизонтально-проеци- |
||||||||||||||
рующую прямую (f H). |
|
|
|
|
|
|
|
|
|
|
У |
|||
|
|
Горизонтально-проецирующая плоскость |
|
|
||||||||||
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Искажённая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
f" |
|
величинаТ |
|
|
|
|
|
|
|
|
|
|
|
|
B" |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
B |
|
|
|
|
|
|
A" |
|
|
Н |
|
|
|
A |
|
|
|
W |
|
|
x |
|
|
|
A" |
|
|
|
|
|
|
|
|
Бφ |
|
||||||
|
|
|
|
C |
|
|
|
|
|
|
||||
|
x |
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B' C' |
|
|
|
|
|
|
C' |
|
|
|
|
αV |
A' |
|
f' |
|
|
|
|
H |
B' |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
й |
Вырожденная |
|
|||||
|
|
A' |
|
|
|
|
иy |
|
|
|||||
|
|
|
|
|
|
проекция плоскости |
|
|||||||
|
|
|
|
|
|
|
|
α(A,B,C) H |
|
|||||
|
|
|
|
|
р |
|
|
|
||||||
|
|
|
|
|
|
|
|
f H |
|
|||||
|
|
а |
|
|
|
б |
|
|
|
|
||||
|
|
|
|
Рис. 3.7 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
о |
|
|
|
|
|
|
|
|
||
|
!!! Запомните характерные |
признаки горизонтально-проецирующей |
||||||||||||
плоскости на чертеже – ее горизонтальная проекция представ- |
||||||||||||||
ляет с б й |
прямуюи(вырожденная проекция αV), наклоненную к оси про- |
|||||||||||||
екций x, и пределяет угол наклона плоскости к плоскости проекций V. Фрон- |
||||||||||||||
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
тальная и р фильная (не показана) проекции плоскости представляют собой |
||||||||||||||
|
|
величинеформу, которой эта плоскость задананачертеже. |
||||||||||||
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Профильно-проецирующая плоскость перпендикулярна профильной |
|||||||||||||
плоскостиппроекций W. На рис. 3.8 плоскость задана двумя параллельными |
||||||||||||||
прямыми KL и MN; фронталь и горизонталь плоскости преобразуются в про- |
||||||||||||||
фильно-проецирующие прямые. |
|
|
|
|
|
|
|
|
|
|
||||
искаженную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
!!! Запомните характерные признаки профильно-проецирующей плос- |
|||||||||||||
кости на чертеже – ее |
профильная |
проекция |
представляет |
|||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
собой прямую (вырожденная проекция δW), наклоненную к осям про- |
||||||||||||||
екций x и y, и определяет углы наклона плоскости к плоскостям проекций |
||||||||||||||
V и H. Фронтальная и горизонтальная проекции этой плоскости представ- |
||||||||||||||
ляют собой искаженную по величине форму, которой эта плоскость задана |
||||||||||||||
на чертеже. |
|
|
|
|
|
|
|
|
|
|
|
|
37 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
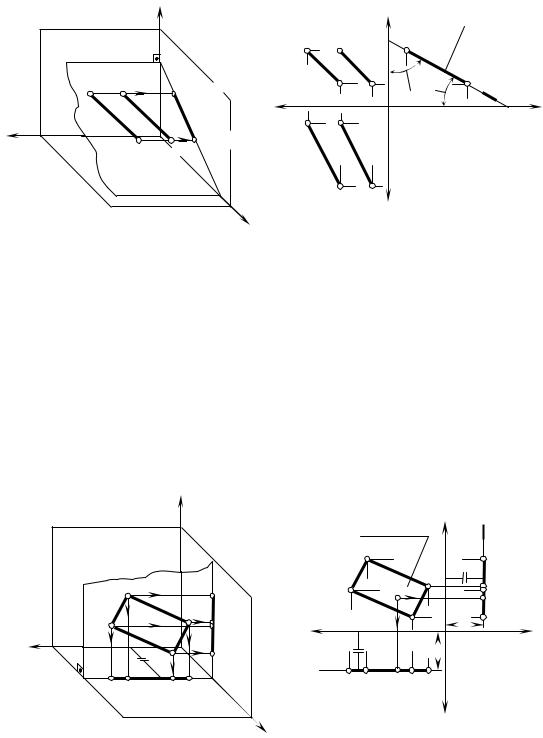
|
|
|
|
|
z |
|
|
|
|
|
|
z |
|
Вырожденная проекция |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
V |
|
|
|
|
|
|
K" |
|
M" |
K'"≡M'" |
|
плоскости |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
K |
M |
|
|
|
|
|
|
|
φV |
φH |
L"≡N'" |
|
||
|
|
|
K'"≡M'" |
x |
N" |
|
L" |
|
δW |
y |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
|
|
|
|
|
W |
|
K' |
|
M' |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
L"≡N'" |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
L |
N |
|
|
|
|
|
|
|
δ(KL // MN) W |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
δ |
|
|
|
|
L' |
|
N' |
y |
|
|
|
|
У |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||
|
|
|
|
|
а |
|
|
|
|
|
|
б |
|
|
|
||
|
|
|
|
|
|
|
Рис. 3.8 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Плоскости частного положения, перпендикулярные двум плоскостям |
|||||||||||||||||
проекций и параллельные третьей плоскости проекций называются плоско- |
|||||||||||||||||
стями уровня. |
|
|
|
|
|
|
|
|
|
|
Н |
|
|||||
Фронтальная плоскость уровня параллельна фронтальной плоскости |
|||||||||||||||||
проекций V и перпендикулярна плоскостям |
БH и W. На рис. 3.9 |
||||||||||||||||
фронтальная плоскость уровня задана параллелограммом DEFG; фронталь- |
|||||||||||||||||
ная проекция этой плоскости является ее натуральной величиной. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
проекций |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
плоскость |
|
|
|
|
|
|
||
|
|
|
|
|
|
z |
|
и |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
||
|
|
V |
|
|
|
|
|
|
Натуральная |
z |
|
βW |
|
||||
|
|
|
|
|
W |
Фронтальная |
|
|
величина |
|
|
E"' |
|
||||
|
|
|
|
|
|
|
|
E" |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
F" |
|
F"' |
|
||||
|
|
|
β |
E |
|
т |
|
D" |
|
|
|
|
|||||
|
|
|
|
|
|
M" |
|
|
|
D"' |
|
||||||
|
|
|
|
|
|
F |
E"' |
|
|
|
|
|
|
|
M"' |
|
|
|
|
|
D |
|
|
F"' |
|
|
|
|
|
|
|
y |
y |
||
|
|
|
|
|
|
x |
|
|
|
G" |
|
G"' |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
|
|
|
|
D"' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
зG |
|
G"' |
|
βH |
|
|
M' |
y |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
β(DEFG) // V |
|||||||
|
|
|
D' E' |
G' F' |
|
|
|
D' E' |
G' F' |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
оH |
|
|
|
y |
|
|
|
|
|
y |
|
( H и W) |
||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
а |
|
|
|
|
|
|
б |
|
|
|
|
|
|||
е |
|
|
|
Рис. 3.9 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
!!! Запомните характерные признаки фронтальной плоскости на чер- |
|||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
теже – ее горизонтальная и профильная проекции про- |
|||||||||||||||||
ецируются |
в прямые (вырожденные проекции βH и βW), параллель- |
||||||||||||||||
ные соответственно осям проекций x и z. |
|
|
|
|
|
|
|
|
|||||||||
Горизонтальная плоскость уровня параллельна горизонтальной плос- |
|||||||||||||||||
кости проекций Н и перпендикулярна плоскостям проекций V и W. |
|||||||||||||||||
38
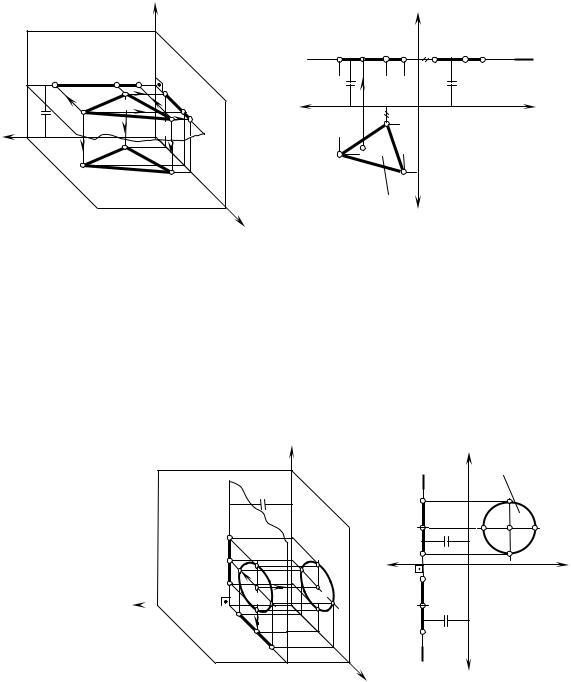
На рис. 3.10 горизонтальная плоскость уровня задана треугольником |
||||||||||||||||||
ABC; горизонтальная проекция этой плоскости является ее натуральной |
||||||||||||||||||
величиной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
!!! Запомните характерные признаки горизонтальной плоскости на |
||||||||||||||||||
чертеже – ее фронтальная и профильная проекции про- |
||||||||||||||||||
ецируются |
в |
|
прямые (вырожденные проекции αV и αW), |
парал- |
||||||||||||||
лельные соответственно осям проекций x и y. |
|
|
|
|
|
У |
||||||||||||
|
|
|
|
|
|
|
Горизонтальная плоскость |
|
|
|
|
|||||||
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
V |
|
|
|
|
|
|
|
|
αV |
A" K" |
B" С" |
B"' |
A"' |
C"' |
||
|
|
|
|
|
|
|
W |
|
|
|
|
αW |
||||||
|
|
A" |
B" |
|
C" |
|
|
|
|
|
|
|
|
|
Т |
|||
|
|
|
B"' |
|
|
x |
|
|
|
|
|
|||||||
|
|
|
A |
B |
|
|
A"' |
|
|
|
|
|
|
|
|
y |
||
|
|
|
|
|
|
|
|
|
B' |
0 |
|
|
|
|||||
x |
|
|
α |
|
|
|
C |
C"' |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
K' |
|
Нα(∆ABC) // H |
||||||
|
|
|
A' |
B' |
|
|
|
|
|
|
A' |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
( V и W) |
||||||
|
|
|
|
H |
|
|
C' |
|
|
|
НатуральнаяБC' |
|
|
|
||||
|
|
|
|
|
|
|
|
y |
|
|
величина |
|
y |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
йб |
|
|
|
|
|||
|
|
|
|
|
|
а |
|
|
Рис. 3.10 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|||
Профильная плоскость ур вня параллельна плоскости проекций W и |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
||
перпендикулярна плоскос ям пр екций V и H. На рис. 3.11 плоскость за- |
||||||||||||||||||
дана кругом с центром в |
|
О и ее профильная проекция имеет нату- |
||||||||||||||||
|
|
|
|
|
|
|
|
очке |
|
|
|
|
|
|
|
|
|
|
ральную величину этого круга. |
|
|
|
|
|
|
|
|
|
|
||||||||
!!! Запомните |
|
|
т |
|
|
|
|
|
|
|
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
||||||||
характерные при- |
|
|
Профильная плоскость |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
знаки пр фильнзй |
|
|
|
z |
|
|
|
|
|
z Натуральная |
||||||||
плоскости на чер- |
|
|
V |
|
|
|
|
|
|
δV |
|
|
величина |
|||||
теже – |
ее фр |
н- |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тальная |
гои - |
|
|
|
|
δ |
|
|
|
|
O" |
|
|
|
|
|||
ризонтальная |
|
|
|
|
|
|
W |
|
|
O"' |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
п |
|
|
|
|
O" |
|
|
|
|
|
x |
|
|
|
y |
||
п р о |
|
к ц и и |
|
|
|
|
|
|
|
|
|
|
|
|||||
представляют |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||
е |
|
|
|
x |
|
|
O |
|
|
O'" |
|
|
|
|
δ // W |
|||
собой прямые |
|
|
|
|
|
|
O' |
|
|
|||||||||
(вырожденные про- |
|
|
|
|
|
|
|
|
|
|
|
( V и H) |
||||||
Р |
|
|
|
|
|
|
|
|
O' |
|
|
|
|
|
|
|
|
|
екции δV и δH), |
|
|
|
H |
|
|
|
|
δH |
|
|
|
|
|||||
перпендикулярные |
|
|
|
|
|
|
|
y |
|
|
y |
|
||||||
оси проекций x и |
|
|
|
|
а |
|
|
|
|
|
|
б |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
параллельные осям |
|
|
|
|
|
|
|
|
Рис. 3.11 |
|
|
|
|
|||||
z и y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39
