17. Гидравлический расчет длинного трубопровода постоянного диаметра

Рас­смотрим три задачи. При построении пьезометрической линии будем учитывать только потери напора по длине.

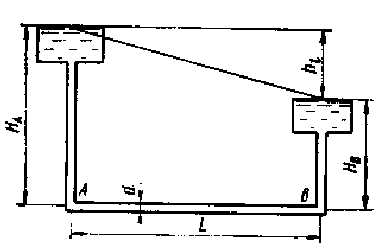
Задача 1. Определение расхода воды Q при заданных d, L, Н_A и Н_B (рис.).

Полная потеря напора в трубе равна:

.

Из формулы

Расходную характеристику К определяют по таблицам в зависимо­сти от d. Длина трубопровода, состоящего из вертикальных труб, иду­щих от бака, существенно меньше длины L .

Задача 2. Определение напора На, который необходимо создать в на­чале трубопровода при заданных d, L, Н_B и Q.

Используя формулу , получим:

Задача 3. Определение диаметра d, необходимого для того, чтобы при за­данных Н_A, Н_B, L, труба могла пропустить расход Q .

Диаметр трубы не входит в явном виде в формулы

Поэтому необходимо найти предварительно К или s₀, зависящие от d.

Из формулы по­лучим:

Найденного значения удельного сопротивления s₀ может не оказать­ся в таблицах. В таком случае можно принять ближайшее большее или ближайшее меньшее значение s₀.

При меньшем значении s₀ труба бу­дет обладать большей пропускной способностью, а при большем s₀ - наоборот.

В первом случае для пропуска заданного расхода потребует­ся регулирование его задвижкой (краном). Во втором случае необходимо увеличить начальный напор На или уменьшить остаточный Н_В.

Окончательный выбор инженерного решения должен быть сделан после его экономического обоснования. Эту задачу можно решить, применяя составной трубопровод. Один участок трубопровода длиной х назначают диаметром, соответствующим ближайшему меньшему зна­чению s₀. Остальной участок трубопровода длиной L - х должен иметь диаметр, соответствующий ближайшему большему значению s₀.

Поте­ря напора в этом случае равна:

Используя формулу , получим:

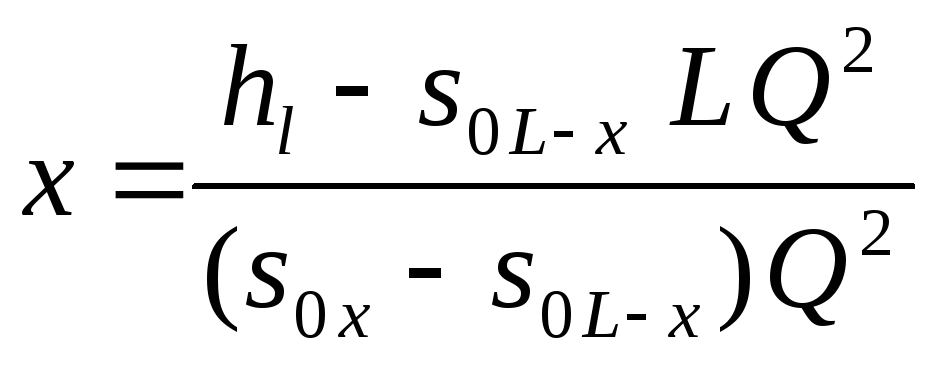
18. Расчет трубопровода с последовательным соединением, параллельным, разветвленным, с непрерывной раздачей жидкости

Различают последовательное и параллельное соединение труб. Рас­смотренный выше случай применения составных труб является од­ним из примеров последовательного соединения труб.

Потери набора при последовательном соединении труб

Рассмотрим два случая:

Случай 1. Расход в системе труб постоянный (рис.). Система труб со­ставлена из трех участков труб длиной L₁ L₃ L₃ и разных диаметров d₁ d₂ d₃ . Заданы начальный и конечный напоры Н_А и Н_в.

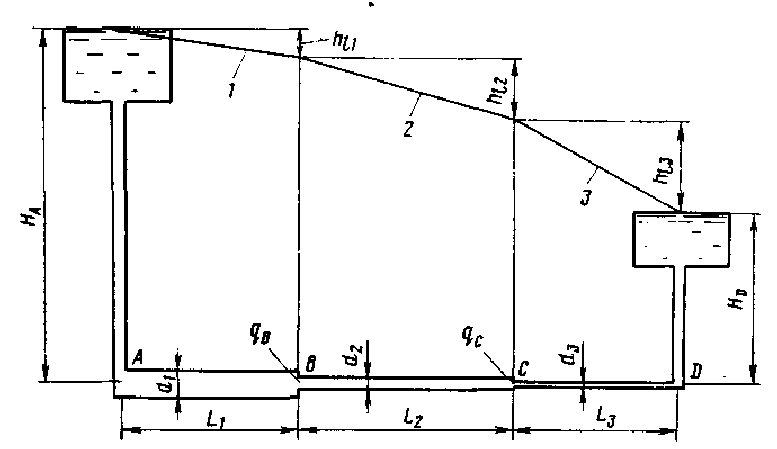
Рис. Схема последовательного соединения труб

Полная по­теря напора в таком трубопроводе складывается из отдельных потерь напора на каждом участке:

С учетом формулы получим:

После подстановки в уравнение удельных сопротивлений и длин найдем расход Q.

Затем вычисляют отдельные потери напора и строят пьезометрическую линию 1 — 2 — 3 (см. рис.) без уче­та местных сопротивлений в пунктах В и С и скоростных напоров.

Напо­ры в пунктах В и С называют свободными напорами.

Случай 2. В системе трубопровода в пунктах В и С имеются отводимые рас­ходы воды q_B q_C (см. рис.).

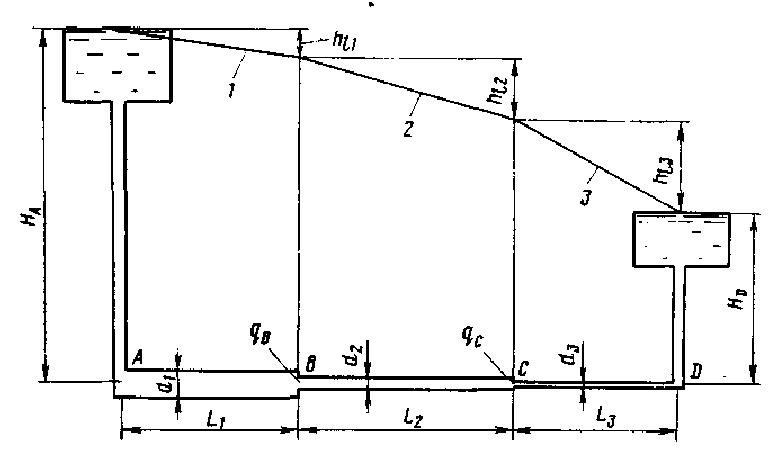
Рис. Схема последовательного соединения труб

Основное уравнение полной потери напора принимает вид (считая, что Q - расход воды в начале системы)

Решение этой задачи аналогично предыдущему решению.

Потери напора при параллельном соединении труб

В этом случае трубы разветвляются с последующим их соединением. Рассмотрим разветвление труб в общей системе последовательного соединения труб (рис.).

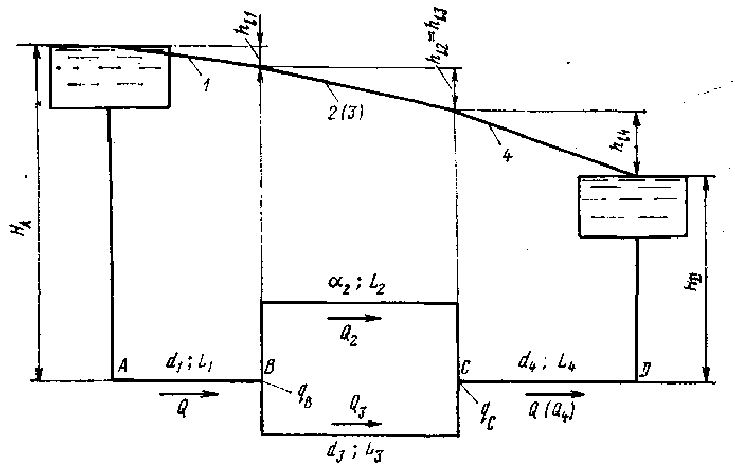
Рис. Схема последовательного и параллельного соединения труб

Задача заключается в том, чтобы определить расход воды, пропускаемой всей системой, и расходы, проходящие в трубах развет­вления, и построить пьезометрическую линию. Поэтому необходимо составить три уравнения.

Характерная особенность параллельного в гид­равлическом смысле соединения трубопроводов - равенство потерь напора в любых трубопроводах (ветвях) между пунктами В и С.

Это объясняется тем, что в пункте В (см. рис.) имеем для всех ветвей об­щий начальный напорН_В и в пунктеС - общий напорН_С.

Выражая потерю напора между пунктами В иС через параметры любой ветви, основное уравнение для всей системы при отсутствии отводимых рас­ходов в пунктахВ и С принимает вид

(*)

Очевидно, вместо второго члена можно поставить .

Составим два других уравнения.

На основании сказанного:

или

(**)

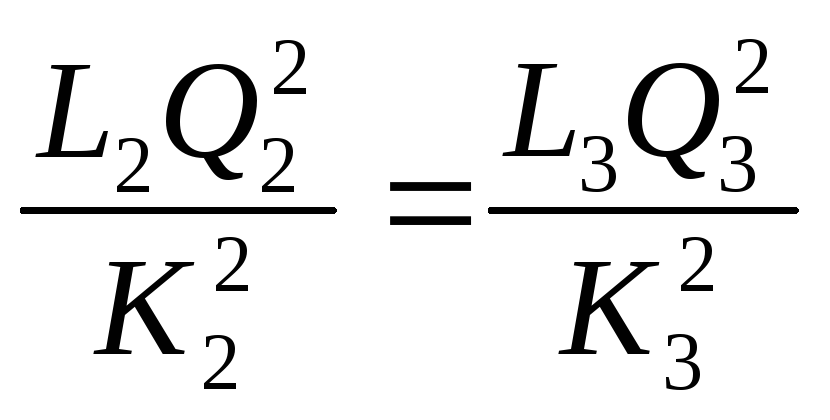Уравнение распределения расходов в системе:

(***)

Решая уравнения (*), (**) и (***), получим Q Q₂ и Q_3.

Для по­строения линии пьезометрических напоров 1 - 2(3) - 4 (см. рис.) необходимо подсчитать потери напора и пьезометрические высоты в сечениях В и С.

Контролем вычислений является равенство:

Аналогично решают задачу, если в пунктах В и С отводится жид­кость с расходами q_B q_C .

Основное уравнение принимает вид:

,

где

На первом участке расход .

Уравнение 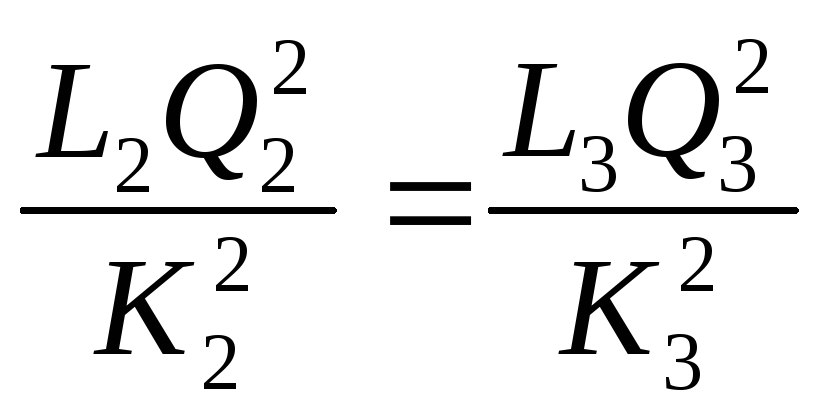по своему виду остается без изменения.

Уравнение распределения расходов получает вид:

Трубопровод при непрерывных и транзитных расходах жидкости

Предположим, что через начальное сечение трубопровода проходит расход жидкости, часть которого пройдет транзитом по всей длине трубопровода. Назовем его транзитным расходом и обозначим Q_T (рис.).

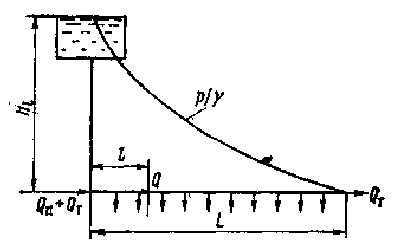
Рис. Схема трубопровода с непрерывным изменением расхода жидкости по длине

Часть расхода непрерывно раздается потребителям. Назо­вем этот расход путевым и обозначим Q_П.

Отношение характеризу­ет интенсивность раздачи расхода на единицу длины трубопровода.

Бу­дем считать, что эта величина не изменяется по длине трубопровода.

В сечении, расположенном на рас­стоянии l от начального сечения, расход равен:

Пьезометрическая ли­ния в данном случае не является прямой (скорости потока изменяются по длине.

Потерю напора по длине рассчитывают по формуле:

С некоторым упрощением это уравнение можно переписать в виде:

При Q_П = 0 (при отсутствии раздачи жидкости по длине трубопровода) получим:

При Q_Т = 0 (весь расход воды роздан на длине трубопровода) получим:

Следовательно, при непрерывной раздаче жидкости в пути требует­ся напор в 3 раза меньший, чем при транзите такого же расхода жид­кости.

Пьезометрическая линия на длине трубы L обычно представляет собой плавную нисходящую кривую (см. рис.) с выпуклостью, об­ращенной вниз.

Это бывает, если:

Если скоростной напор вдоль трубопровода убы­вает более интенсивно, чем уменьшение напора, обусловленного поте­рями энергии, то пьезометрическая линия будет представлять собой восходящую кривую.