Матрицы операторов

Пусть в некоторой фиксированной координатной системе ,известны матрицы,операторовA, B, соответственно.

Определим матрицу оператора , гдепокажем, что.

Имеем

. ▼

Пусть , тогда

.

.

Отсюда .

Итак, имея базис , мы поставили в соответствие каждому линейному операторуA матрицу , тогда

.

Соответствие взаимнооднозначное, и матрица является матрицей некоторого оператора, то есть если, то

.

Таким образом, если , то

.

Подведем итоги, пусть ,и т.д. множество всех матриц. Определим сумму, умножение на число, произведение,– матрицу нулевого оператора,– матрицу тождественного оператора формулами

, ,

, ,

Тогда соответствие между всеми линейными операторами A на L и всеми матрицами , задаваемыми как, является изоморфизмом.

Пример VI.3. Пусть A линейный оператор на множестве многочленов степени не большей, чем n1, ,, определенный формулойи– базис вM, определенный формулой ,. Найти матрицу оператораA, где в базисе.

Решение. Если ,, то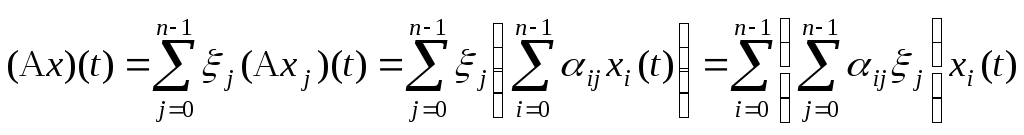

Отсюда ,. Применяя формулу бинома Ньютона,, для каждого фиксированногоj, приравнивая коэффициенты при одинаковых степенях , получим

.

Учитывая, что , причемдля, где, получим матрицу оператораA

, .

В частности, для случая

. ▼

Покажем, как, зная матрицу линейного оператораA по координатам вектора x, найти координаты образа Ax в этом базисе.

Пусть , тогда, в обозначениях примера,, что равносильно матричному равенству

, (VI.4)

где в квадратных скобках стоит произведение вектора (можно матрицы-строки) на матрицу оператора A.

Отсюда следует, что строка координат вектора равна строке координат вектора x, умноженной справа на матрицу , все в базе .

Пример VI.4. В условиях предыдущего примера, найти координаты образа при известной, где.

Решение. Имеем , тогда. По-прежнему ограничимся случаем, где базис, тогда

.

Окончательно,

. ▼

Изменение базиса 3, 11

Дадим ответ на решение задач, часто возникающих при изменении базиса.

Пусть ,,, – два базиса вn-мерном линейном пространстве L.

I (a). Если вектор , то какова связь между его координатами в базисеи его координатамив базисе?

I (b). Если – упорядоченное множество скаляров, то какова связь между векторамиx и y?

Пусть A – линейный оператор, определяемый равенствами

,

положим ,, тогда.

Ответы:

(a). Пусть – матрица оператораA в базисе , то есть,. ОператорA обратим, поскольку из , следует, что,. Так как

,

то

.

(b). Очевидно, что . Это означает следующее: если матрицаоператораA известна, то ее строки можно рекомендовать рассматривать как преобразование координат, а можно как преобразование векторов.

Подобие 11

II (a). Пусть B – линейный оператор на L. Какова связь между его матрицами ив базисахисоответственно?

II (b). Дана матрица . Какова связь между линейными операторамиB и C, определенными равенствами исоответственно?

Ответы:

a) Имеем ,. С использованием оператораA можем записать

.

А также

.

Учитывая предыдущее выражения, стоящие в правых частях, получаем

.

Или, переходя к матрицам, имеем равенство

.

Матрица соответствует операторуB в базисе и для ее вычисления, учитывая, что операторA обратим, умножим слева матричное уравнение на матрицу . Учитывая, что

и ,

получаем

.▼

В этом случае говорят, что матрицы иподобны.

б). Заметим, что и

,

то есть оператор C таков, что

или

, тогда .

Линейные операторы C и B называются подобными, если существует обратимый оператор A, удовлетворяющий этому равенству.

Пример VI.5. Доказать, что а) если A подобен скаляру , то ;b) если A и B подобны, то это же верно и для и, а еслиA и B обратимы, то подобны и и.

Решение. а) Пусть E – тождественный оператор, тогда, по определению, . Далее существует операторC, что , тогдаи, по теореме об обратимости оператора,, то есть.▼

b) имеем , тогда

. ▼

Пусть A и B обратимы, тогда имеем . Заметим, что для любых обратимых матриц,, тогда

. ▼