
- •В.А. Павский линейная алгебра
- •Оглавление
- •Введение
- •I. Введение в линейную алгебру § 1. История развития алгебры
- •§ 2. Множества
- •§ 3. Строение множеств
- •Алгебра множеств
- •§ 4. Число Развитие
- •§ 5. Числовые множества
- •Бесконечные множества
- •Натуральный ряд
- •Множество целых чисел
- •Множество рациональных чисел
- •Множество действительных чисел
- •Множество комплексных чисел
- •Суммы и произведения
- •Приближенные вычисления
- •II. Элементы линейной алгебры § 1. Матрицы и определители 3, 7
- •Действия над матрицами
- •1. Сложение матриц
- •2. Умножение матрицы на число
- •3. Умножение матриц
- •Определитель матрицы
- •Свойства определителей
- •Вычисление определителей
- •Аксиоматическое построение теории определителей
- •Обратная матрица
- •Ранг матрицы
- •Элементарные преобразования матрицы
- •§ 2. Системы линейных алгебраических уравнений
- •Методы решения слау
- •1. Метод Крамера
- •2. Матричный метод
- •3. Метод Гаусса
- •Однородная система линейных алгебраических уравнений (ослау)
- •§ 3. Системы линейных алгебраических неравенств
- •III. Линейные пространства
- •§ 1. Линейная зависимость
- •§ 2. Линейные комбинации. Базисы
- •§ 3. Подпространства
- •§ 4. Прямые суммы
- •§ 5. Евклидовы пространства
- •§ 6. Координатные системы
- •IV. Векторная алгебра § 1. Векторы
- •§ 2. Линейные операции над векторами
- •§ 3. Проекция вектора на ось
- •Линейные свойства проекции вектора на ось
- •Координаты вектора
- •Деление отрезка в данном отношении
- •§ 4. Базис системы векторов
- •§ 5. Скалярное произведение векторов
- •§ 6. Векторное произведение векторов 4
- •Геометрические свойства векторного произведения
- •Алгебраические свойства векторного произведения
- •§ 7. Смешанное произведение векторов 4
- •V. Аналитическая геометрия 4
- •§ 1. Системы координат на плоскости
- •§ 2. Уравнение линии на плоскости
- •§ 3. Уравнение поверхности и линии в пространстве
- •§ 4. Прямая и плоскость в линейном пространстве
- •Уравнение плоскости, проходящей через три точки
- •Взаимное расположение плоскостей
- •Уравнение прямой в пространстве r3
- •Уравнение прямой, проходящей через две точки
- •Прямая как линия пересечения плоскостей
- •Расстояние от точки до прямой
- •Угол между прямой и плоскостью
- •Угол между плоскостями
- •VI. Линейные операторы § 1. Линейный оператор
- •Векторные свойства линейных операторов
- •Умножение операторов
- •Матрицы операторов
- •Изменение базиса 3, 11
- •Подобие 11
- •§ 2. Характеристический многочлен
- •VII. Билинейные и квадратичные формы § 1. Билинейные формы
- •§ 2. Квадратичные формы
- •Приведение к каноническому виду
- •VIII. Гиперповерхности и поверхности второго порядка
- •Классификация линий второго порядка
- •Окружность
- •Гипербола
- •Парабола
- •Классификация поверхностей второго порядка
- •Заключение
- •Список литературы
- •Линейная алгебра
- •650002, Г. Кемерово, ул. Институтская, 7
- •650002, Г. Кемерово, Институтская, 7
Уравнение плоскости, проходящей через три точки
Пусть
даны три точки
![]() ,
,![]() и
и![]() .
Если точки не лежат на одной прямой, то
через них всегда можно провести
единственную плоскость. Обозначим (х,
у,
z)
координаты произвольной точки М
пространства и рассмотрим три вектора:
.
Если точки не лежат на одной прямой, то
через них всегда можно провести
единственную плоскость. Обозначим (х,
у,
z)
координаты произвольной точки М
пространства и рассмотрим три вектора:
![]() ,
,![]() ,
,![]() .
ТочкаМ
лежит на плоскости М1М2М3
в том и только в том случае, когда
перечисленные три вектора компланарны,
а значит
.
ТочкаМ
лежит на плоскости М1М2М3
в том и только в том случае, когда
перечисленные три вектора компланарны,
а значит
![]() ,
т.е. определитель, составленный из их
координат, равен нулю:
,
т.е. определитель, составленный из их
координат, равен нулю:
 .
.
Пример
V.5.
Написать уравнение плоскости, проходящей
через точки
![]() ,
,![]() и
и![]() .
.
Решение.
Пусть
![]() – произвольная точка плоскости,
тогда
векторы
– произвольная точка плоскости,
тогда
векторы![]() ,
,![]() ,
,![]() компланарны, поэтому:
компланарны, поэтому:
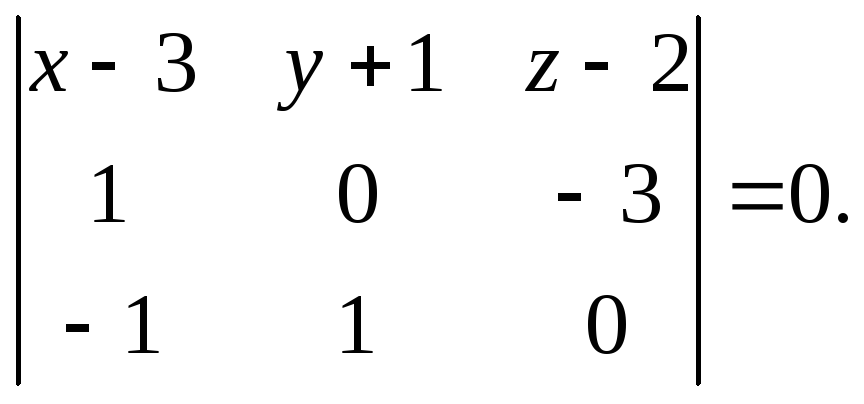
Вычисляя
определитель по правилу треугольников,
получим:![]() или
или![]() .
.
Теорема
V.1.
В пространстве
![]() всякая плоскость выражается уравнением
первой степени
всякая плоскость выражается уравнением
первой степени
![]() ,
,![]() .
.
Доказательство. В предыдущем пункте было установлено, что всякая плоскость может быть задана уравнением вида (V.4):
![]() ,
,
![]() .
.
Раскрыв
скобки и обозначив
![]() ,
получим общее уравнение первой степени
относительноx,
y,
z:
,
получим общее уравнение первой степени
относительноx,
y,
z:
![]() ,
эквивалентное уравнению (V.4).
Поэтому оно определяет ту же плоскость,
что и уравнение (V.4),
и называется общим
уравнением плоскости.
Коэффициенты при переменных в этом
уравнении сохраняют тот же геометрический
смысл, что и в равенстве (V.4),
то есть являются координатами нормального
вектора
,
эквивалентное уравнению (V.4).
Поэтому оно определяет ту же плоскость,
что и уравнение (V.4),
и называется общим
уравнением плоскости.
Коэффициенты при переменных в этом
уравнении сохраняют тот же геометрический
смысл, что и в равенстве (V.4),
то есть являются координатами нормального
вектора
![]() плоскости. Так как нормальный вектор
плоскости является ненулевым, то
коэффициентыA,
B
и C
не могут быть одновременно равны нулю.
Итак, мы доказали, что всякая плоскость
в
плоскости. Так как нормальный вектор
плоскости является ненулевым, то
коэффициентыA,
B
и C
не могут быть одновременно равны нулю.
Итак, мы доказали, что всякая плоскость
в
![]() определяется уравнением первой степени
относительно переменных координат x,
y,
z.
определяется уравнением первой степени
относительно переменных координат x,
y,
z.
Теорема
V.2
(обратная).
Всякое
линейное уравнение с тремя переменными
![]() ,
,![]() ,
определяет плоскость в пространстве
,
определяет плоскость в пространстве
![]() ,
если хотя бы один из коэффициентов при
переменных не равен нулю.
,
если хотя бы один из коэффициентов при
переменных не равен нулю.
Доказательство.
Пусть x0,
y0,
z0
– какое-либо решение данного уравнения.
Тогда
![]() ,
откуда
,
откуда![]() .
Подставляя в данное уравнение вместоD
его значение и группируя члены, получим
.
Подставляя в данное уравнение вместоD
его значение и группируя члены, получим
![]() .
.
Это
уравнение плоскости, проходящей через
точку
![]() и имеющей нормальный вектор
и имеющей нормальный вектор![]() .
Следовательно, и равносильное ему
уравнение
.
Следовательно, и равносильное ему
уравнение![]() определяет плоскость [перпендикуляр-ную
вектору
определяет плоскость [перпендикуляр-ную
вектору![]() ].
].
Пример
V.6.
Построить
в прямоугольной системе координат
плоскость, заданную уравнением
![]() .
.
Решение.
Для построения плоскости необходимо и
достаточно знать какие-либо три ее точки
(не лежащие на одной прямой), например
точки пересечения плоскости с осями
координат. Полагая в заданном уравнении
![]() ,
получим
,
получим![]() .
Следовательно, заданная плоскость
пересекает осьOz
в точке
.
Следовательно, заданная плоскость
пересекает осьOz
в точке
![]() .
Аналогично, при
.
Аналогично, при![]() получим
получим![]() ,
то есть точку
,
то есть точку![]() ;
при
;
при![]() получим
получим![]() ,
то есть точку
,
то есть точку![]() .
По трем точкам
.
По трем точкам![]() ,
,![]() ,
,![]() строим заданную плоскость (рис.V.6).
строим заданную плоскость (рис.V.6).
Частные случаи общего уравнения плоскости. Рассмотрим особенности расположения плоскости в тех случаях, когда те или иные коэффициенты общего уравнения обращаются в нуль.
1.
При
![]() уравнение
уравнение![]() определяет плоскость, проходящую через
начало координат, так как координаты
точки
определяет плоскость, проходящую через
начало координат, так как координаты
точки![]() удовлетворяют этому уравнению.
удовлетворяют этому уравнению.
2.
При
![]() уравнение
уравнение![]() определяет плоскость, параллельную осиОх,
поскольку нормальный вектор
определяет плоскость, параллельную осиОх,
поскольку нормальный вектор
![]() этой плоскости перпендикулярен осиОх
(его проекция на ось Ох
равна нулю). Аналогично при
этой плоскости перпендикулярен осиОх
(его проекция на ось Ох
равна нулю). Аналогично при
![]() плоскость
плоскость![]() параллельна осиОу,
а при
параллельна осиОу,
а при
![]() плоскость
плоскость![]() параллельна осиОz.
параллельна осиОz.
3.
При
![]() уравнение
уравнение
![]() определяет плоскость, проходящую через
ось Ох,
поскольку она параллельна оси Ох
(
определяет плоскость, проходящую через
ось Ох,
поскольку она параллельна оси Ох
(![]() )
и проходит через начало координат (
)
и проходит через начало координат (![]() ).
Аналогично плоскость
).
Аналогично плоскость
![]() проходит через ось Оу,
а плоскость
проходит через ось Оу,
а плоскость
![]() – через ось Оz.
– через ось Оz.
4.
При
![]() уравнение
уравнение
![]() определяет плоскость, параллельную
координатной плоскости Оxу,
поскольку она параллельна осям Oх
(
определяет плоскость, параллельную
координатной плоскости Оxу,
поскольку она параллельна осям Oх
(![]() )
и Оу
(
)
и Оу
(![]() ).
Аналогично, плоскость
).
Аналогично, плоскость
![]() параллельна плоскости уОz,
а плоскость
параллельна плоскости уОz,
а плоскость
![]() – плоскости Оxz.
– плоскости Оxz.

Рис. V.6
5.
При
![]() уравнение
уравнение![]() (или
(или
![]() )
определяет координатную плоскость Оxу,
так как она параллельна плоскости Оxу
(
)
определяет координатную плоскость Оxу,
так как она параллельна плоскости Оxу
(![]() )
и проходит через начало координат (
)
и проходит через начало координат (![]() ).
Аналогично уравнение
).
Аналогично уравнение![]() в пространстве определяет координатную
плоскостьОxz,
а уравнение
в пространстве определяет координатную
плоскостьОxz,
а уравнение
![]() – координатную плоскостьОyz.
– координатную плоскостьОyz.
Пример
V.7.
Составить
уравнение плоскости P,
проходящей через ось Оу
и точку
![]() .
.
Решение.
Уравнение плоскости, проходящей через
ось Оу,
имеет вид
![]() .
Для определения коэффициентовA
и C
воспользуемся тем, что точка
.
Для определения коэффициентовA
и C
воспользуемся тем, что точка
![]() принадлежит плоскостиP.
Поэтому ее координаты удовлетворяют
написанному выше уравнению плоскости:
принадлежит плоскостиP.
Поэтому ее координаты удовлетворяют
написанному выше уравнению плоскости:
![]()
![]() ,
откуда
,
откуда![]() .
Подставив найденное значениеA
в уравнение
.
Подставив найденное значениеA
в уравнение
![]() ,
получим:
,
получим:![]() ,
или
,
или![]() .
.
Это и есть искомое уравнение.
