Свиркина - Учебное пособие 2 семестр матан ЭФ СПбГУ
.pdf
Задача 2.1.23. (неопределенный интеграл, интегрирование по частям, вывод рекуррентной формулы)
Вычислить интеграл ex sin xdx .
Подсказка.
1.Обозначим искомый интеграл за I.
2.Интегрирование по частям u ex , dv sin xdx .
3.Получим рекуррентную формулу 2 .
Ответ: e2x sin x cos x C .
Задача 2.1.24. (неопределенный интеграл, интегрирование по частям, вывод рекуррентной формулы)
Вычислить интеграл 
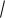4 x2 dx .
Подсказка. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разбить |
на части u |
|
4 x2 ,dv dx . Во втором интеграле в |
|||||||||||||
числителе добавить и отнять 4. Прийти к рекуррентной формуле. |
||||||||||||||||
|
x |
|
|
2arcsin |
x |
|
|
|
|
|
||||||
Ответ: |
4 x2 |
C . |
|
|||||||||||||
|
|
|
||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
||||||
п.5. Интегрирование рациональных дробей. |
|
|||||||||||||||
1. |
Интегралы вида |
|
|
|
|
dx |
|
|
|
берутся путем выделения |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
ax2 bx c |
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
полного квадрата из квадратного трехчлена. |
|||||||||||||||
|
|
|
|
|
|
|
|
Ax B |
|
|||||||
2. |
Интегралы вида |
|
dx берутся путем выделения |
|||||||||||||
ax2 bx c |
||||||||||||||||
в числителе производной квадратного трехчлена стоящего в знаменателе и раскладыванием на сумму двух интегралов.
32
Задача 2.1.25. (неопределенный интеграл, интегрирование рациональных дробей)
dx
Вычислить интеграл x2 6x 25 .
Подсказка.
25 9 16 .
Ответ: 1 arctg x 3 C .
4 4
Задача 2.1.26. (неопределенный интеграл, интегрирование рациональных дробей)
Вычислить интеграл |
3x 1 |
|
|
||||||||
|
|
dx . |
|
|
|||||||
x2 4x 8 |
|
|
|||||||||
Подсказка. |
|
|
|
|
|
|
|
|
|||
3x 1 |
3 |
|
2x 4 1 6 . |
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
||
Ответ: |
3 |
ln x2 4x 8 |
5 |
arctg |
x 2 |
C . Модуль под |
|||||
2 |
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
||||
логарифмом снят, т.к. квадратный трехчлен всюду положительный.
Задача 2.1.27. (неопределенный интеграл, интегрирование рациональных дробей с помощью разложения на простейшие дроби)
Вычислить интеграл |
|
x2 2x 6 |
|
|
||||||||
|
|
|
|
|
dx . |
|
||||||
x 1 x 2 x 4 |
|
|||||||||||
Подсказка. |
|
|
|
|
|
|
|
|
|
|
||
|
x2 2x 6 |
|
A |
|
B |
|
C |
|
|
|||
|
|
|
|
|
|
|
|
|
. Привести |
правую |
||
|
x 1 x 2 x 4 |
x 1 |
x 2 |
x 4 |
||||||||
часть к общему знаменателю, |
сравнить коэффициенты при |
x2 , при x |
||||||||||
и без x . Найти A, B, C и взять интегралы. |
|
|
||||||||||
|
|
|
|
|
|
33 |
|
|
|
|
|
|
Ответ: ln x 1 3 x 4 5 C .
x 2 7
Домашняя работа (четыре номера)
Задача 2.1.28. (неопределенный интеграл, интегрирование по частям)
Вычислить интеграл x2ex dx .
Подсказка.
u x2 , dv ex dx .
Ответ: ex x2 2x 2 C .
Задача 2.1.29. (неопределенный интеграл, интегрирование по частям)
Вычислить интеграл arcsin xdx .
Подсказка.
u arcsin x, dv dx .
Ответ: x arcsin x 
1 x2 C .
Задача 2.1.30. (неопределенный интеграл, замена переменной, интегрирование по частям, вывод рекуррентной формулы)
Вычислить интеграл 
x2 dx .
Подсказка.
Разбить по частям. Прийти к рекуррентной формуле.
|
1 |
|
|
|
|
|
|
Ответ: |
|
2 |
ln |
x |
|||
|
x |
x |
|
||||
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x |
2 |
|
C . |
|
|
|
|||
|
|
|
|
|
|
|
|
|
34
Задача 2.1.31. (неопределенный интеграл, интегрирование рациональных дробей)
Вычислить интеграл |
5x 3 |
dx . |
|
||||||
|
|
|
|
||||||
x2 4x 8 |
|
||||||||
Ответ: |
5 |
ln x2 |
4x 8 |
7 |
arctg |
x 2 |
C . |
||
|
|
|
|||||||
|
2 |
|
2 |
|
2 |
|
|||
35
ЗАНЯТИЕ 6. Интегрирование простейших иррациональных дробей. Вычисление определенных интегралов. Несобственные интегралы.
Аудиторная работа
Проверка домашнего задания (2.1.28, 2.1.29, 2.1.30, 2.1.31)
(продолжение) Глава 2. Интегральное исчисление.
(продолжение) §1 Неопределенный интеграл.
п.6. Интегрирование простейших иррациональных дробей.
1. |
Интегралы вида |
|
|
|
|
dx |
берутся путем выделения |
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
ax2 |
bx c |
|||||||||||
|
|
|
|
|
||||||||
|
полного квадрата из квадратного трехчлена. |
|||||||||||
2. |
Интегралы вида |
|
|
Ax B |
|
|
dx берутся путем |
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|||||||||
|
|
|
|
ax2 bx c |
||||||||
выделения в числителе производной квадратного трехчлена стоящего в знаменателе и раскладыванием на сумму двух интегралов.
3. Интегралы вида |
|
|
dx |
|
берутся с помощью |
|
|
|
|
|
|||
x |
|
|
||||
ax2 bx c |
||||||
|
|
|
||||
подстановки x 1t .
Задача 2.1.32. (неопределенный интеграл, интегрирование иррациональных дробей)
Вычислить интеграл |
|
|
dx |
|
. |
|
|
|
|
|
|||
|
|
|
||||
x2 2x 5 |
||||||
|
|
|
||||
Подсказка.
5 1 4 .
36
Ответ: ln x 1 
x2 2x 5 C .
Задача 2.1.33. (неопределенный интеграл, интегрирование иррациональных дробей)
Вычислить интеграл |
|
|
5x 3 |
dx |
||
|
|
|
|
|||
|
|
|
||||
2x2 8x 1 |
||||||
|
|
|||||
Подсказка. 5x 3 54 4x 8 13
|
5 |
|
|
|
13 |
|
ln |
x 2 |
|
1 |
|
|
||
Ответ: |
|
2x2 8x 1 |
x2 4x |
|
C |
|||||||||
2 |
|
|
|
2 |
||||||||||
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 2.1.34. (неопределенный интеграл, интегрирование иррациональных дробей)
Вычислить интеграл |
|
|
dx |
|||||
|
|
|
|
|||||
|
|
|
|
|||||
|
|
|
|
x |
5x2 2x 1 |
|||
Подсказка. x |
1 |
, dx |
1 |
dt |
||||
|
t |
|
t 2 |
|||||
|
|
|
|
|
|
|||
Ответ: ln 1 x 
5x2 2x 1 C x
§2 Определенный интеграл.
п.1. Вычисление определенных интегралов
b
f x dx F x ba F b F a - формула Ньютона-Лейбница.
a
37
Задача 2.2.1. (определенный интеграл)
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Вычислить интеграл 2x2 |
5x 6 dx |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Ответ: |
19 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задача 2.2.2. (определенный интеграл) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вычислить интеграл |
|
3 x3 x 1 |
dx |
|
|||||||||||||
|
|
x2 |
1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Подсказка. |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
, arctg1 |
. |
|
|
||||||||||
arctg |
|
|
3 |
|
|
||||||||||||
|
|
3 |
|
|
|
|
4 |
|
|
|
|
||||||
Ответ: 1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
12 |
|
|
|
|
|
|
|
|
|
||||||||
п.2. Несобственные интегралы. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
f x dx lim |
f x dx |
|
|
(2.1) |
||||||||||||
a |
|
|
|
|
|
|
b |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
f x dx lim |
f x dx |
|
|
(2.2) |
||||||||||||
|
|
|
|
|
|
|
a |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
f x dx lim |
f x dx |
|
|
(2.3) |
||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b a |
|
|
|
|
|
|
|
|
|||
Определение. Если пределы в (2.1) - (2.3) и конечны, |
то |
||||||||||||||||
несобственный интеграл называется сходящимся, если предел |
или |
||||||||||||||||
равен , то расходящимся. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38 |
|
Определение. |
Если функция f x имеет |
бесконечный разрыв в |
||||||
c a, b |
и |
непрерывна |
при a x c |
и |
c x b , |
то |
по |
|
определению полагают |
|
|
|
|
|
|
||
b |
|
c |
|
b |
|
|
|
|
f x dx lim |
f x dx lim |
f x dx |
|
|
(2.4) |
|||
0 |
|
0 |
c |
|
|
|
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
Определение. |
|
Несобственный |
интеграл |
f x dx , |
|
где |
||
f c ,при a c b |
|
|
|
a |
|
|
||
называется сходящимся если |
|
оба |
||||||
предела в правой части (2.4), и расходящимся, если (равен ) хотя бы один из них.
Формула (2.4) для случаев разрыва в границах интегрирования a и b приобретает следующий вид
b |
|
|
f b |
|
b |
|
|
|
|||||
|
f x dx |
|
|
lim |
f x dx |
|
(2.5) |
||||||
a |
|
|
|
|
|
0 |
a |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|||
b |
|
|
f a |
b |
|
|
|
||||||
|
f x dx |
|
|
lim |
f x dx |
|
(2.6) |
||||||
a |
|
|
|
|
|
0 |
a |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
Задача 2.2.3. (несобственный интеграл) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
dx |
|
|
Исследовать на сходимость несобственный интеграл |
. |
||||||||||||
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Подсказка. |
|
|
|
|
|
|
|
|
|||||
В |
|
x 0 |
функция не |
ограничена по |
(2.5) имеем |
||||||||
1 |
dx |
|
1 |
dx |
|
|
|
|
|
||||
|
lim |
|
(или |
можно рассмотреть |
односторонний |
||||||||
|
|
||||||||||||
0 |
|
x |
|
0 |
0 |
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
предел при a 0 ).
39
Ответ: интеграл расходится.
Задача 2.2.4. (несобственный интеграл)
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследовать на сходимость несобственный интеграл e |
x dx . |
|
||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
||
Подсказка. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
b |
|
|
|
|
|
Используем (2.1), т.е. |
e |
|
x dx lim |
e |
x |
dx Далее |
берем |
|||||
|
|
|
0 |
|
|
b |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
неопределенный |
интеграл |
заменой |
переменной |
|||||||||
|
|
|
Интеграл 2 te t dt берем |
|
|
|||||||
t |
x, x t 2 , dx 2tdt . |
по |
частям |
|||||||||
u t, dv e t dt . В пределе применяем Правило Лопиталя .
Ответ: 2 интеграл сходится.
Задача 2.2.5. (несобственный интеграл)
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|||||
Исследовать на сходимость несобственный интеграл |
|
|
|
|
|
. |
|
|
|||||||||
1 |
x |
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подсказка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
dx |
|
|
|||||||
Т.к. подынтегральная функция четная, то |
|
|
|
|
2 |
|
|
|
|
. При |
|||||||
1 |
x |
2 |
|
1 |
x |
2 |
|||||||||||
|
|
|
|
|
|
0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
взятии предела учитываем график функции см. Рис 8.
40
Рис. 8
Ответ: интеграл сходится.
Задача 2.2.6. (несобственный интеграл)
1 dx
Исследовать на сходимость несобственный интеграл x2 .
Ответ: 1 интеграл сходится.
Домашняя работа (три номера) (к Занятию 8)
Задача 2.1.35. (неопределенный интеграл, интегрирование иррациональных дробей)
dx
Вычислить интеграл 
.
3x2 4x 1
Подсказка.
Тройку вынести, привести к простейшему интегралу вида
|
|
dx |
|
|
|
|
|
arcsin |
x |
C . |
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
a |
||||
a2 x2 |
||||||||||||
Ответ: |
|
1 |
|
arcsin 3x 2 C . |
||||||||
|
|
|
|
|||||||||
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
||||
41