18. Вырождение динамических систем типа «многомерный вход – многомерный выход»

Понятие вырождение в переводе с англ. (degeneration, degeneracy) означает дегенерация, ослабление качеств, упадок и т.д. При рассмотрении динамических систем типа «многомерный вход – многомерный выход» (МВМВ) вырождение стоит понимать как снижение работоспособности системы, которое может возникнуть в силу следующих обстоятельств. Система может вырождаться структурно (конфигурационно), когда из ее состава выпадает некоторый функциональный элемент. Причины вырождения могут носить организационный характер, когда формируемые целевые намерения неудачно распределяются по входам каналов многомерной динамической системы. Вырождаться могут системы по причине параметрической природы, когда неудачно организованы связи между каналами системы, неудачно назначены показатели характеристик этих связей, когда неудачно сформированы полосы пропускания каналов, а в случае, если система имеет дискретную природу, неудачно назначены и распределены по каналам интервалы дискретности и т.д.

Склонность системы к вырождению может повлечь за собой сбой в нормальном ее функционировании, а зачастую привести к частичной или даже полной потери работоспособности системы. Для того, чтобы «предвидеть» возникновение критической ситуации, необходимо априорное исследование системы на предмет возможного вырождения.

Технология контроля вырождения сложных непрерывных и дискретных динамических технических систем с многомерным входом–выходом, изложенная в настоящем учебном пособии, основана на использовании сепаратных и глобальных функционалов вырождения, конструируемых на спектре сингулярных чисел матрицы линейного оператора сложной системы, отображающего входное пространство целевых намерений в выходное пространство их реализаций. При этом поток намерений может носить детерминированный и стохастический характер, характеризоваться равномерным или произвольным распределением по входам системы.

Формирование матриц линейных операторов в зависимости от детерминированного или стохастического характера входного потока опирается на формализм матричных уравнений Сильвестра и Ляпунова. Представленная технология позволяет дать численную оценку функционалов вырождения, при которой сложная динамическая техническая система оказывается близкой к частичной или полной потери работоспособности.

18.1. Вырождение многомерной динамической системы как сокращение ранга линейного оператора отношения вход-выход

Вырождение многомерной динамической системы (МДС) будем рассматривать в математической постановке как сокращение ранга линейного оператора отношения вход-выход, отображающего пространство входов (целевых намерений) в пространство выходов (осуществляемых реализаций), матричное представление которого с помощью критериальной матрицы сводит задачу к контролю ранга этой матрицы. Ранг матрицы как одна из ее численных характеристик является величиной целочисленной, а процесс изменения ранга по существу оказывается скачкообразным. В этой связи для осуществления математического мониторинга процесса изменения свойств линейного оператора при подходе к скачкообразному изменению ранга необходимо на параметрах матрицы линейного оператора сформировать некоторый характеристический показатель, который обладает свойством непрерывного изменения своего значения при скачкообразном изменении ранга. Таким свойством обладает характеристический показатель в форме числа обусловленности матрицы оператора и конструируемый на нем функционал вырождения.

Пусть задана многомерная динамическая система, реализующая некий линейный оператор с матрицей , отображающий пространство входов в пространство выходов так, что становится справедливой линейная алгебраическая задача (ЛАЗ) вида:

, (18.1)

где –­– матрица для любых значений,;,–-мерные векторы;- принимает смысл непрерывного времени, когда ЛАЗ (18.1) параметризована непрерывным временем, и смысл дискретного времени, выраженного в числе интервалов дискретности длительности, когда ЛАЗ (18.1) параметризована дискретным временем;–-мерный параметр, изменяющий алгебраические свойства матрицы, принимающий смысл частотыпри спектральном гармоническом представлении внешнего воздействия.

Будем рассматривать ЛАЗ как инструментальную модель контроля вырождения на нормах матрицы и обратной к ней. Для оценки степени вырождения сложной динамической системы воспользуемся такой матричной характеристикой как число обусловленности.

Число обусловленности матрицы в силу определения 3.4 главы 3 запишем в следующей форме

. (18.2)

Из выражения (18.2) видно, что численно число обусловленности зависит от выбранной матричной нормы. Заметим, что наибольшими инструментальным богатством и геометрической прозрачностью содержательной интерпретации числа обусловленности обладает в решаемой задаче спектральная норма, что будет использовано в дальнейшем.

Если в выражении (18.2) для матричных компонентов воспользоваться спектральными нормами

, ,

то число обусловленности, построенное на спектральных нормах примет вид

(18.3)

где ,– соответственно максимальное и минимальное сингулярные числа матрицы.

Опираясь на положения утверждения 13.1 главы 13, сформулируем представление о геометрической интерпретации ЛАЗ (18.1), которое состоит в том, что вектор отражается в подпространство, натянутое на-ый элементлевого сингулярного базисатак, что соответствующий ему вектор имеет норму, равную. Таким образом, линейное алгебраическое соотношение (18.1) решает задачу отображения единичной сферыв эллипсоид, оси которого принадлежат подпространствам, натянутым на элементы левого сингулярного базиса, а длины этих полуосей равны сингулярным числам матрицы.

Эволюция процесса вырождения матрицы , характеризующаяся бесконечным ростом её числа обусловленности, записанного в форме (18.3) сопровождается деформацией исходной сферыпутем преобразования ее в эллипсоид, «сплющиванием» этого эллипсоида сначала вдоль его-той полуоси, принадлежащей линейной оболочке, натянутой на-тый элементлевого сингулярного базиса, затем «сплющиванием» его вдольполуоси и т.д. так, что будет наблюдаться последовательное «сплющивание» эллипсоида вдоль векторов,…. В итоге сфера отобразится в эллипсоид единичной размерности, т.е. в отрезок прямой. Система оказывается на границе глобального вырождения. В том случае, когда все сингулярные числа становятся нулевыми, констатируется глобальное вырождение линейной алгебраической задачи, которое характеризуется тем, что сфера отображается в точку.

Спектр сингулярных чисел и сконструированные на нем числа обусловленности матрицы указывают механизм численного контроля процесса вырождения при вариации времениw и параметров с помощью контроля чисел обусловленности, последовательно устремляющихся к бесконечным значениям.

Для иллюстрации геометрической интерпретации процесса вырождения матрицы путем сплющивания эллипсоидных образов единичной сферы рассмотрим пример.

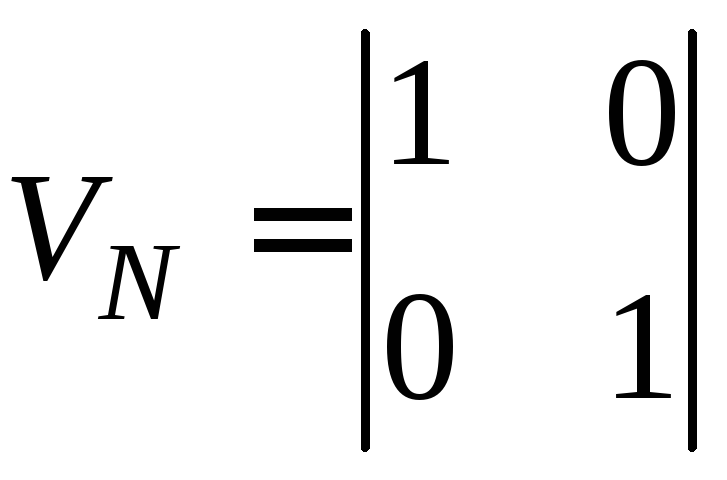Пример 18.1. Представим реализацию матриц в обобщенном виде, где- матрица левого сингулярного базиса,- матрица правого сингулярного базиса, такие, что главная ось эллипсоида развернута на уголотносительно оси абсцисс; - диагональная матрица с сингулярными числами и . Для наглядной иллюстрации результатов предлагаемого примера угол выберем различным.

Исследуемые матрицы для фиксированных значенийи соответствующие им числа обусловленности сведем в таблицу 18.1.

Таблица 18.1

1		9		2
2		43		5
3		11	20
4		20	50
5		120	200
6		85

Результаты отображения единичной сферы, гдев эллипсоид для реализации матрицc различными числами обусловленности приведены на рисунке 18.1.

Рисунок 18.1. Отображение единичной сферы в эллипсоид для различных

значений числа обусловленности : 1 - ; 2 - ;

3 - ; 4 - ; 5 - ; 6 - .

На рисунке 18.1 наглядно просматривается процесс «сплющивания» эллипсоида в прямую линию с увеличением значения числа обусловленности матрицы .

В силу определения (18.2) числа обусловленности подчинены следующим неравенствам

. (18.4)

Однако, контроль близости числа обусловленности к бесконечной величине является достаточно сложной задачей. В связи с этим возникла необходимость построения непрерывного аналога целочисленной оценки вырождения линейной алгебраической задачи, процесс отслеживания которого был бы более простым.

Введем в рассмотрение величину обратную числу обусловленности, назвав ее функционалом вырождения , который зададим соотношением

. (18.5)

Соотношение (18.5) с учетом (18.4) позволяет записать для функционала вырождения следующие неравенства:

. (18.6)

Следует заметить, что решение задачи заметно обогатится, если помимо функционала вырождения (18.5), контролируются также и сепаратные функционалы вырождения с индексом линейной алгебраической задачи (18.1) с матрицей, конструируемые на алгебраическом спектре сингулярных чисел этой матрицы в силу соотношения

, (18.7) (2)

где , – соответственно максимальное и -ое сингулярные числа матрицы , вычисляемые с помощью соотношений

; (18.8)

. (18.9)

Заметим, что функционал вырождения (18.5) оказывается функционалом вырождения с индексом равным единице.

Таким образом, процесс вырождения ЛАЗ (18.1) можно отслеживать по последовательному обнулению функционалов вырождения , контроль граничных значений которых в пределах 0 и 1 заметно проще контроля граничных значений чисел обусловленности в пределах 1 и .

Введенные сепаратные функционалы вырождения позволяют ввести следующие определения.

Определение 18.1. Линейная алгебраическая задача (18.1) характеризуется индексом вырождения равным единице, если нулевым является только функционал вырождения с индексом единица. □

Определение 18.2. Вырождение линейной алгебраической задачи (18.1) характеризуется индексом вырождения равным , если оказываются нулевыми все функционалы вырождения с индексами от 1 до. □

Из последнего определения 18.2. нетрудно сделать вывод, что при линейная алгебраическая задача оказывается награнице глобального вырождения, при этом линейный оператор с матрицей отображает единичную сферу в отрезок прямой, длина которого определяется единственным ненулевым сингулярным числом, а положение в пространстве определяется первым элементом левого сингулярного базиса матрицы. Заметим, что в приведенном примере этому случае соответствует шестой вариант реализации матрицы(см.таблицу 18.1 и рисунок 18.1).Система оказываетсяглобально вырожденной когда в нуль обращаются все сепаратные функционалы вырождения, в этом случае линейный оператор с матрицей отображает единичную сферу в ноль.

Контроль вырождения линейных алгебраических задач (18.1) параметризованных параметрами w и , которые могут принимать значения непрерывного и дискретного времени, а также частоты, с помощью сепаратных функционалов вырождения делают значения последних также параметризованными непрерывным и дискретным временем, а также частотой, что позволяет выделять временные интервалы и диапазоны частот, характеризующиеся различной степенью вырожденности многомерной динамической системы. Таким образом, контроль вырождения многомерной динамической системы при заданном модельном описании потока входных заявок может быть осуществлен с помощью алгоритма.