35782

Согласно второму закону механики эта равнодействующая сила равна произведению массы элемента ρdV на ускорение ddvτx , т.е.

Приравнивая (2.35) и (2.36) и произведя сокращение на dv, получим

Таким же образом могут быть получены уравнения и для проекций равнодействующих сил на оси y и z. В результате получится система из трех уравнений.

Это и будет дифференциальное уравнение движения несжимаемой вязкой жидкости в проекциях на оси координат, или уравнение Навье-Стокса. В векторной форме это уравнение имеет вид

Рассмотрим частный случай уравнения Навье-Стокса для невязкого течения (μ=0)

Полагая в (2.38) μ=0, получим уравнение Эйлера

для невязкого течения жидкости.

2.4. Вязкость жидкости. Закон Ньютона для вязкости

Известно, что в деформируемых твердых упругих телах имеет место закон Гука, согласно которому деформация пропорциональна нагрузке. Согласно закону Стокса, жидкость имеет непрерывную деформацию, она течет со скоростью, которая возникает с нагрузкой. На рис.2.4 на расстоянии y друг от друга изображены две параллельные плоскости внутри движущегося объема жидкости. Причем нижняя плоскость движется со скоростью v, а верхняя – v+ v.

Рис. 2.4. Ламинарное течение жидкости между двумя параллельными пластинами.

21

Введем понятие касательного напряжения τт , оно равно силе на единицу площади, которую надо приложить к пластине, чтобы поддержать постоянную скорость

Этот закон носит название закона Ньютона для трения, параметр μ - динамическая вязкость жидкости. Сила F=ma и единицей измерения силы является Ньютон (Н)

Существует понятие кинематической вязкости

Оба эти понятия широко применяются в гидродинамике. Существуют жидкости чрезвычайно высокой вязкости, например, жидкий асфальт, вулканическая лава, вазелин и др. Для таких понятий закон Ньютона (2.40) не выполняется, поэтому они называются неньютоновскими, для них справедлив закон

где n – эмпирическая величина.

2.5. Свободное движение жидкости вдоль вертикальной стенки

Рассмотрим процесс движения вдоль вертикальной нагреваемой пластины, расположенной в неограниченном пространстве (рис. 2.5).

Рис. 2.5. Свободная конвекция вдоль вертикальной стенки: а) ламинарный и турбулентный пограничные слои; б) распределение температуры t и скорости Vx по толщине δ пограничного ламинарного слоя.

В этих условиях вдоль пластины снизу вверх движется тонкий слой жидкости, а основная масса жидкости остаётся в состоянии покоя (рис. 2.5,а). На некоторой высоте ламинарный пограничный слой разрушается и

22

переходит в турбулентный. На рис. 2.5,б показано распределение температуры перегрева ϑ и скоростей v по толщине пограничного слоя.

Составим для ламинарного пограничного слоя уравнение движения для случая, когда разность давлений отсутствует. Определим объёмную силу Х, вызывающую движение жидкости из-за перепада температуры ϑ (температура перегрева):

где g x - составляющая гравитационного ускорения в направлении Х; ρ∞ , ρ

– плотность удалённой от поверхности среды и плотность среды в пограничном слое.

нагретой пластины.

Уравнение движения (2.37) для пограничного слоя при свободной конвекции примет вид

Глава 3. Теория подобия

3.1. Постановка задачи

Из-за ограниченных возможностей аналитического решения дифференциальных уравнений большое значение приобретает эксперимент. Однако, число экспериментальных данных как правило, велико, и требуются методы обобщения опытных данных. Одно из средств решения этой задачи – теория подобия, которая по существу является теорией эксперимента. При постановке любого эксперимента необходимо заранее знать:

какие величины надо измерять в опыте; как обрабатывать результаты опыта;

какие явления подобны изучаемому, т.е. на какие случаи можно распространять полученные зависимости. Ответы на эти вопросы даёт теория подобия, к изложению которой переходим.

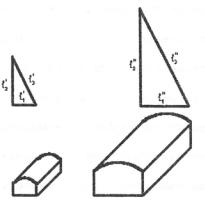
Впервые с понятием подобия встречаемся в геометрии, в которой введено понятие геометрически подобных фигур. Например, изображённые на рис. 3.1 фигуры и треугольники обладают следующим свойством: их соответствующие углы равны, а соответствующие стороны пропорциональны, т.е.

23

Рис. 3.1 Подобие различных геометрических фигур

где l1,l2 ,l3 − линейные размеры фигур; штрихи ( ׳) и ( ״) относятся к

обозначениям первой и второй фигуры; С – коэффициент пропорциональности, или константа подобия. Условие (3.1) – математическая формулировка геометрического подобия фигур. Оно справедливо для любых сходственных отрезков подобных фигур: высот, медиан и других.

Понятие подобия можно распространять и на физические явления. Можно, например, говорить о подобии движения двух потоков жидкости, так называемое кинематическое подобие; подобие сил – динамическое подобие; о подобии температур – тепловое подобие. Понятие подобия в отношении физических величин применимо только к явлениям одного рода, которые качественно одинаковы и аналитически описываются одними уравнениями и по форме, и по содержанию. Если аналитические уравнения двух каких-либо одинаковых по форме, но различных по физическому содержанию, то такие явления называют аналогичными. Такая аналогия существует, например, между явлениями кондуктивной теплопроводности и переноса электрического заряда в проводниках. Основной закон и в том, и в другом случае формулируется одинаково: удельные потоки теплоты q , плотности электрического тока j пропорциональны градиенту температуры – grad t , градиенту электрического потенциала – grad U (законы Фурье и Ома).

где λ и σ – коэффициенты пропорциональности, т.е. коэффициент теплопроводности и электропроводности. Хотя выражения (3.2) одинаковы по форме, но по содержанию они совершенно различны. Это позволяет явления переноса теплоты и электричества отнести к явлениям аналогичным.

24

3.2. Условия физического подобия

Подобие двух физических явлений означает подобие всех величин, характеризующих рассматриваемые явления, т.е. любая величина первого явления ϕ′ пропорциональна однородной с ней величине ϕ′′ второго

времени.

Рассмотрим, например, общий случай движения жидкости. По определению величина скорости u есть отношение пути l ко времени τ движения, т.е. v= l/ τ. Применим формулу (3.3) к двум подобным потокам жидкости:

Уравнения (3.4) выражают условия подобия, которым ограничивается произвольный выбор констант подобия Cu ,Cl ,Cτ . Обозначение idem в

уравнении (3.4) означает “одно и то же”. Уравнение (3.4) характеризует кинематическое подобие и показывает, что в подобных системах существуют особые величины, называемые инвариантами, или критериями подобия, или числами подобия. Критерии подобия – безразмерные комплексы, составленные из величин, характеризующих явление.

Рассмотрим условия динамического подобия. Согласно второму закону Ньютона, сила F равна массе m, умноженной на ускорение а: F= m· а= m·( v/ τ). Применим преобразования (3.3), в этом случае

F=m·a=m·(v /τ), (F·τ)/(m·v)=idem=Ne,

(Cu Cm ) /(Cl Cτ ) =1.

Критерии подобия принято называть именами учёных, работавших в этой области, и обозначать двумя начальными буквами их фамилии, например, Ne (Newton) критерий Ньютона.

Критерий подобия можно получить для любого физического явления. Для этого необходимо иметь аналитическую зависимость между переменными рассматриваемого явления. Это необходимая предпосылка теории подобия. В тех же случаях, когда рассматривается новый процесс, для которого аналитического описания ещё нет, критерии подобия выделяются на основе анализа размерностей, познакомиться с которым

25

можно в специальной литературе. Отметим, что комбинации из чисел подобия дают новое число подобия.

3.3. Теоремы подобия

Основные положения теории подобия формулируются в виде трёх теорем.

Первая теорема подобия: подобные между собой явления имеют одинаковые критерии подобия.

Вторая теорема подобия: зависимость между переменными, характеризующими явления, может быть представлена в виде зависимости между критериями подобия K1 , K2 ,…, Kn :

Зависимость (3.6) называется критериальным уравнением. Помимо критериев подобия в это уравнение могут входить так называемые симплексы – безразмерные отношения однородных физических величин.

Третья теорема подобия: подобны те явления, условия однозначности которых подобны и критерии, составленные из условий однозначности, численно одинаковы.

Условия однозначности состоят из начальных и граничных условий задачи, или краевых условий. Критерии, полученные из этих условий, называются определяющими. Возможна такая формулировка третьей теоремы подобия: явления подобны, если определяющие критерии инвариантны (одинаковы).

Критерии, составленные из величин, не входящих в условия однозначности, называются неопределяющими. Когда устанавливается подобие, то неопределяющие критерии сами собой получаются также одинаковыми. Следовательно, теория подобия позволяет, не интегрируя дифференциальных уравнений, получить из них критерии подобия и из опытных данных установить критериальные зависимости, последние будут справедливы для всех подобных между собою процессов.

В начале этого раздела были сформулированы основные три вопроса, которые стоят перед экспериментатором. Теперь можно дать ответ на эти вопросы.

На первый – о том, какие величины надо измерять в опыте – отвечает первая теорема подобия: в опытах надо измерять величины, которые содержатся в критериях подобия изучаемого явления.

На второй вопрос – как обрабатывать результаты опыта – отвечает вторая теорема подобия: результаты опытов надо представлять в виде критериальных зависимостей.

На третий вопрос – какие явления подобны – ответ дает третья теорема подобия: подобны те явления, у которых подобны условия однозначности и равны определяющие критерии.

26

3.4. Определение критериев подобия из дифференциальных уравнений

Приведем иллюстрацию этого метода на примере одномерного стационарного (∂ϑ / ∂τ = 0 ) уравнения движения (2.38):

Представим это уравнение через размерности входящих в него параметров. При этом обозначим размерности скоростей vx и vy через v, размерность

отрезков x, y – через L, получим

разделим все члены уравнения на левую часть

В последнее равенство вошли искомые критерии:

Согласно второй теореме подобия опытные данные надо обрабатывать в

Уравнение энергии для однородного стационарного уравнения (∂ϑ / ∂τ = 0 ) в несжимаемой жидкости (div vr = 0 ) при умеренных скоростях имеет вид:

Комбинируя критерии Рейнольдса и Пекле, получим критерий Прандтля, являющиеся физической константой:

Pr =νa = физическаяфизическаяконстантаконстанта = физическаяконстанта - критерий Прандтля

Аналогичным образом рассмотрим уравнение для коэффициента теплоотдачи

λ ∂t a = − ∂y t − tw

27

которое приведем к виду

[1]= aL .λ

Комплекс aLλ (безразмерный коэффициент теплоотдачи) носит название критерия Нуссельта:

Критерий подобия для естественной конвекции можно получить, комбинируя критерии Рейнольдса и Фруда:

его называют критерием Галилея. Умножая критерий Галилея на симплекс

носящий название критерия Архимеда. Так как при естественной конвекции неоднородность поля плотности вызывается неоднородностью

температуры, то параметрический критерий ρ −ρρ0 замещается выражением

который носит название критерия Грасгофа.

Интенсивность теплообмена при естественной конвекции может быть определена с помощью уравнения

3.5. Критерии подобия

Основные трудности дальнейшего анализа конвективного теплообмена связаны с установлением вида функциональной зависимости (3.6). Эта задача для простейших случаев может быть решена аналитически, но в большинстве случаев вид этих функциональных зависимостей устанавливается при обобщении экспериментальных данных.

Изложим основные принципы, на которых основаны методы обобщения данных эксперименты по изучению конвективного теплообмена. Предположим, что экспериментально в условиях естественной конвекции удалось измерить коэффициент теплообмена проволок разного диаметра в различных средах при различных значениях

28

температурных напоров. При обработке экспериментальных данных были получены серии зависимостей (3.6), связывающих коэффициенты теплообмена с отдельными параметрами (диаметром, температурным напором, свойствами среды, геометрическими параметрами L и т.д.), т.е.

Эти зависимости носят частный характер и

справедливы только для тех условий, при которых проводились опыты. Однако существует возможность эти частные результаты применить для расчета коэффициента теплообмена иных (в отличие от изучаемого) случаев теплообмена проволок. Например, исследования проводились в воздухе на проволоках диаметром 0.5 – 3 мм при температурном напоре - 150 С. Если эти данные опыта обрабатывать на основе теории подобия, то возможно полученные зависимости использовать для определения коэффициента теплообмена проволоки диаметром 0.1 или 5 мм в водороде при температурном напоре до 150 С.

Изложим основные положения теории подобия. Протекание сложных физических процессов характеризуется не отдельными физическими и геометрическими величинами, а некоторыми безразмерными комплексами или так называемыми критериями подобия, составленными из этих величин. Например, на теплообмен при естественной конвекции существенное влияние оказывают около десятка физических величин, входящих в зависимость (3.6). Если на основе теории подобия объединить физические и геометрические параметры в безразмерные комплексы, тот же процесс можно описать не десятью, а тремя следующими критериями:

Здесь через L обозначен геометрический параметр, характерный для тела данной конфигурации (диаметр для труб или шаров, высота плиты и т.д.).

Пусть в результате исследования коэффициента теплоотдачи проволок при разных значениях диаметров (L), температурных напоров (t − tc ) и в различных средах (λ,β,ν,α) получен набор значений

коэффициента теплоотдачи. На основании этих эмпирических данных вычисляются значения критериев Gr, Pr, Nu и устанавливается эмпирическая функциональная зависимость типа (3.16). Забегая вперед, заметим, что для явлений естественной конвекции часто удается получить эту зависимость в более простом виде, а именно:

29

т.е. вместо двух аргументов (Gr,Pr) можно, как показывает опыт, в данном случае обойтись одним аргументом (Gr·Pr).

Допустим, что произведение критериев Gr·Pr изменялось в рассматриваемых опытах в диапазоне 1 ≤ Gr Pr ≤103 .

Покажем, что формулу (3.18) можно применить для большого числа иных (нежели изучаемого) случаев теплообмена проволоки, т.к. величину комплекса Gr·Pr в пределах от 1 до 103 можно получить при самых различных значениях параметров, входящих в критерии Gr и Pr.

Если опыты проводились только в воздухе с цилиндрами разных диаметров и при этом произведение Gr·Pr изменялось в пределах от 1 до 103 , то полученные результаты можно использовать для расчета комплекса Nu для цилиндра d=5мм в водородной среде, т.к. значение Gr·Pr не выходит за пределы, полученные в опытах с воздухом. В частности, меняя температуры t и tc или диаметр цилиндра, можно подобрать значение

Gr·Pr=400. Если будет известен вид функциональной зависимости (3.18), то можно рассчитать критерий Nu, а затем из (3.18) определить значение коэффициента теплообмена для рассматриваемых цилиндров в воздушной и водородной средах.

Итак, показана возможность обобщения результатов отдельных опытов. Следует помнить, что в нашем частном примере критериальная зависимость (3.18) справедлива для значений аргументов 1 ≤ Gr Pr ≤103 и ее нельзя использовать в расчетах α, например, при Gr Pr =105 . Этим определяются границы применимости эмпирической формулы.

Следовательно, теория дает возможность ответить на следующие важные вопросы, возникающие при планировании эксперимента, обработке опытных данных и использовании эмпирических результатов: какие величины надо измерять в опыте; как обрабатывать результаты опыта; в каких пределах можно пользоваться полученной эмпирической зависимостью.

Покажем на примере отличие качественно одинаковых и неодинаковых физических процессов. Естественная конвекция между твердой поверхностью и различными жидкими и газообразными средами

30