35782

где v′x - мгновенная скорость.

Пусть это условие соблюдается также для составляющих скорости vy и vz . Степенью турбулентности будем называть величину.

Рассмотрим процесс движения жидкости вдоль пластины (рис.1-3)

Рис. 1.3. Гидродинамическая картина обтекания пластины потоком жидкости

толщина слоя становится больше критической (при x = xкр ), течение в слое

становится неупорядоченным, вихревым; образуется турбулентный пограничный слой с ламинарным подслоем. Переход из ламинарного режима в турбулентный происходит постепенно, и этот режим течения обычно называют переходным.

Рассмотрим течение жидкости в канале (трубе) (рис 1-4)

Рис 1.4. Характер движения жидкости в трубах

Условия в канале (трубе) вблизи входа подобны условиям на продольно обтекаемой пластине. У внутренней поверхности трубы также образуется пограничный слой, толщина которого у входного края трубы равна нулю, а затем постепенно возрастает, как это показано на рис. 1.4. Предположим, что условия входа таковы, что движение частиц в трубе происходит без

11

возмущения. На определённом расстоянии от входа пограничный слой утолщается настолько, что заполняет всё сечение. Кривая распределения скоростей в направлении потока дальше этой точки не меняется и имеет форму параболы (ламинарное течение) либо более сложной выпуклой кривой (турбулентное течение). При поток называется

установившимся. Для установившегося потока, как будет показано ниже, при Re = vvd ≥ 2300 ламинарное течение переходит в турбулентное.

1.2. Местный и средний коэффициенты теплообмена

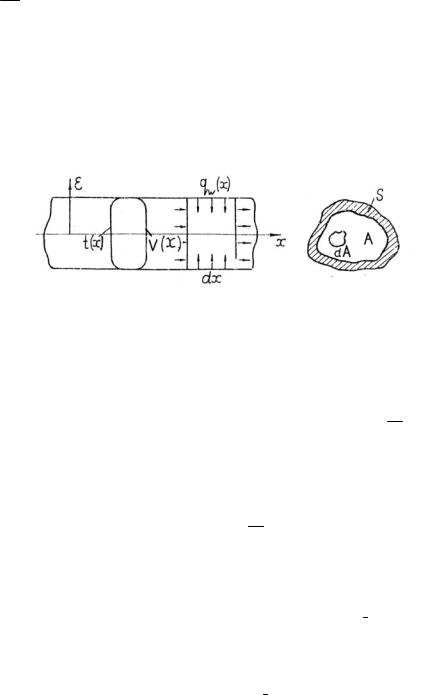
Рассмотрим канал произвольного сечения A и периметра S ; распределение температур и скоростей по сечению представлено на рис.1.5 кривыми t(x), v(x). На стенках канала имеется источник или сток энергии q, с удельной мощностью qw (x) .

Рис 1.5. К определению коэффициентов теплообмена

Найдем тепловой поток d 2Ф1 , который уносится жидкостью от стенки через сечение dА канала на длине dx. Переносимый движущейся жидкостью тепловой поток равен произведению удельной теплоемкости

C p на массовый расход G и на изменение температуры ∂∂xt dx жидкости. В

рассматриваемом случае массовый расход через элемент сечения dА равен произведению плотности ρ на объемный расход v(x)dA , а изменение температуры жидкости на отрезке dx равно dt, тогда

d 2Ф1 = Cp ρv(x) ∂∂xt dxdA .

Через все сечение А переносится поток dФ1 :

A

и преобразуем выражение (1.4): dФ1 = CpGdt ,G = ∫ρv(x)dA. Здесь G – массовый

A

расход жидкости. Через стенки трубы на отрезке длиной dx в жидкость поступает поток dФ2 :

12

(1.11), (1.12) дают возможность определить осредненное по периметру значение α.

Рассмотрим теперь некоторые способы осреднения коэффициента

Коэффициент теплообмена, отнесенный к средней интегральной разности температур,

Средний коэффициент теплообмена, отнесенный к начальной разности температур,

αн = A(tФw w−t0 )

Выбор того или иного способа определения α произволен и должен определяться характером изучаемой задачи. Подставим в (1.13) значение из (1.11):

α = 1 CpG ∫l dt . l A 0 tw −t

Если положить tw = const , то интегрирование выполняется просто:

Умножим и разделим это уравнение на (tl − t0 ) и примем во внимание (1.7), тогда

где tл - средняя логарифмическая разность температур.

В заключение заметим, что средние коэффициенты теплообмена, отнесенные к средней логарифмической (αл ), средней интегральной (αи ) и

определенных по одному способу, к значениям, определенным по другому способу.

При движении жидкости в трубе α, определенное по (1.11), обычно изменяется по длине участка от x=0 до x = lнт , при x > lнт , где lнт - длина

термического начального участка, т.е. на протяжении остальной части

14

трубы, - сохраняет постоянное значение. Это постоянное значение α будем обозначать α∞ .

Глава 2. Дифференциальное уравнение переноса массы, энергии, импульса

2.1. Уравнение массообмена

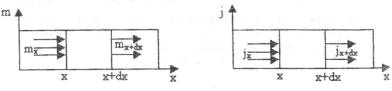
Рассмотрим поток жидкости в одном направлении х (рис. 2.1).

Рис. 2.1. Количество и поток массы при одномерном движении

Выделим в движущемся потоке массы (рис. 2.1) некоторый объём с сечением 1 м2 . На расстоянии х в это сечение входит количество вещества mx , а через сечение (х+ х) – выходит mx+ x , разница между ними m -

изменение плотности. Применим закон сохранения количества вещества и запишем его в форме:

В уравнении (2.6) присутствуют две искомые величины: плотность потока j и удельный вес ρ, и для перехода к одной искомой величине необходимо

15

знать связь между ними. Эту связь дает закон Фика: плотность потока

Знак (-) вызван следующими соображениями: по законам физики перенос вещества осуществляется от мест с большей концентрацией к местам с меньшей концентрацией, а в математике за положительное направление изменения функции принято направление от меньших ее значений к большим. Для того, чтобы снять противоречие между определениями в физике и математике, в уравнение (2.7) подставим знак (-). Коэффициент D в уравнении (2.7) носит название коэффициента диффузии, он имеет

порядков.

Обобщенный закон Фика относится к движущейся жидкости, а закон (2.7)

– к покоящейся. Если имеет место движущаяся жидкость, то к молекулярному механизму переноса вещества накладывается конвективный, т.е. к зависимости (2.7) надо прибавить массовый перенос

Составим дифференциальное уравнение массопереноса Подставим (2.8) в уравнение (2.6), получим

Последнее выражение можно представить в форме

т.е. получим дифференциальное уравнение массопереноса для движущейся в направлении оси x жидкости. По аналогии напишем два уравнения для жидкости, «движущейся» в направлениях y и z.

Складывая уравнения (2.9) и (2.10) придем к случаю, когда жидкость движется в направлениях (x, y, z), и применяя формулы векторного анализа из математики, можем прийти к дифференциальному уравнению массообмена в векторной форме.

Напомним некоторые уравнения векторного анализа. Полная производная ddτ по времени равна

16

Если применить к (2.9), (2.10) определения (2.11), то дифференциальное уравнение массопереноса в векторной форме приобретет вид

Частные случаи дифференциального уравнения массообмена.

По определению несжимаемая жидкость имеет нулевую дивергенцию скорости, т.е.

Если при этом коэффициент диффузии не будет зависеть от координат, т.е. D=const, то его можно вынести за операцию div и

2.2. Уравнение теплопроводности

Это уравнение выводится на основе закона сохранения энергии. Выделим в движущемся потоке жидкости элементарную трубку в

форме удлиненного по оси x параллелограмма. Тепловой поток в этом

17

Запишем (2.18) с использованием понятия удельный тепловой поток q = ФА

Здесь мы столкнулись с проблемой, рассмотренной в предыдущем разделе: поток тепла направлен от более высокой к более низкой температуре, а за положительное изменение функции в математике принимают ее рост от меньших к большим значениям. Этим обстоятельством вызван знак (-) в уравнении (2.19). Второй проблемой является наличие в уравнении двух неизвестных q и t. Связь между ними содержится в законе Фурье: перенос удельного потока энергии q молекулярным механизмом пропорционален

градиенту температуры ∂∂nt в направлении нормали n, т.е.

где λ - коэффициент теплопроводности материала.

Здесь знак (-) вызван теми же соображениями, что и формуле (2.7). Коэффициент теплопроводности, [λ] = мВтК ,может меняться на 5 порядков

0,01 < λ <103 .

Для движущейся жидкости применяют обобщенный закон Фурье

В данном уравнении первый член отвечает за молекулярный механизм переноса, а второй – за конвективный.

Формулы (2.20) и (2.21) связывают удельный поток q теплоты и температуру t, и их можно использовать для преобразования уравнения (2.19). Для этого подставим (2.21) в уравнение (2.19).

После перестановки отдельных членов этого уравнения получим

Если движение жидкости описывается не одной координатой x, а тремя – (x,y,z), то аналогичные рассуждения следует провести для направлений y и z:

Складывая выражения (2.22), (2.23) и применяя формулы векторного анализа (2.11), получим уравнение теплопроводности в векторной форме

18

При наличии источника энергии мощности P в объеме V уравнение (2.24) примет вид

Частные случаи уравнения теплопроводности

1.Источники отсутствуют, коэффициент теплопроводности λ=const Уравнение (2.25) примет вид

Здесь через а обозначен коэффициент температуропроводности тела

2.Несжимаемая жидкость div v = 0 , источники отсутствуют Р=0, λ=const Получаем наиболее распространенный вид уравнения теплопроводности

2.3.Уравнение движения

Вуравнении (2.24) наряду с температурой имеются еще три переменные vx , vy , vz т.е. температурное поле в движущейся жидкости

зависит от распределения скоростей. Последнее описывается дифференциальным уравнением движения, вывод которого основан на втором законе Ньютона: сила равна массе, умноженной на ускорение.

а)б)

Рис. 2.3. К выводу дифференциального уравнения движения жидкости (а); сила трения, действующая на элемент движущейся жидкости (б).

19