
Сборник 70 студ конференции БГТУ
.pdf
411
Составим уравнение прямой АS по двум точкам:
По формуле: |
sin |
|
|
Am B n C p |
|
|
||
|
|
|
|
|||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 B2 C2 m2 n2 p2 |
|
||||||
|
|
|
|
|||||
вычисляем угол между плоскостями треугольника АВС и прямой АS.
Работа выполнена под руководством асс.каф. «Высшая математика» К.А.Раковой
А.В. Бойков МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ДЛЯ ОЦЕНКИ
ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Объект исследования – построение оценок параметров распределения методом максимального правдоподобия.
Автором рассмотрен пример построения оценки для вероятности биномиального распределение.
Метод максимального правдоподобия в математической статистике — это метод оценивания неизвестного параметра путём максимизации функции правдоподобия.
Обозначим через 








 вероятность того, что в результате испытания
вероятность того, что в результате испытания
дискретная случайная величинаX примет значения 
 (i=1,2,..,n).
(i=1,2,..,n).
Функцией правдоподобия случайной дискретной величиныX называют
функцию |
|
аргумента : |
= |
, |
||
где |
— фиксированные числа, полученные при измерении случайной |
|||||
величины. |
|
|
|
|
|
|
В |
качестве |
точечной |
оценки |
параметра принимают такое |
||
его значение |
|
, |
при |
котором функцияправдоподобия |
||
достигает |
максимума. |
Оценку называют оценкой |
максимального |
|||
правдоподобия. |
|
|
|
|
|
|


413
И.В. Бондарева
ОЦЕНКА МЕРЫ ИРРАЦИОНАЛЬНОСТИ ЧИСЛА log3
Объект исследования: вещественное число 
 =log3.
=log3.
Результаты, полученные лично автором: произведен расчет оценки меры иррациональности числа  =log3.
=log3.
Мерой иррациональности µ(τ) вещественного числа τ называется нижняя грань множества чисел λ, для которых, начиная с некоторого положительного 













 , выполняется неравенство
, выполняется неравенство
Первоначально результат оценки меры иррациональности числа ln3 был
установлен А. |
Бэйкером и составлял . В 1987году Д. Рин[1] получил |
новую оценку |
с использованием арифметического метода. |
Данный результат оставался лучшим на протяжении двадцати лет. В 2007 году В. Х. Салиховым [2] был введен новый аналитический метод, который заключается в использовании интеграла, подынтегральная функция которого обладает свойством симметрии. Таким образом, была получена оценка 












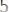 . В дальнейшем результат был улучшен К. Ву[3] и составил
. В дальнейшем результат был улучшен К. Ву[3] и составил






















 . В данной работе для вычислений используется алгоритм, с помощью которого было получено последнее на данный момент значение
. В данной работе для вычислений используется алгоритм, с помощью которого было получено последнее на данный момент значение
меры иррациональности. |
|
Теорема 1: для любого |
существует положительное целое число |
такое что |
|
Таким образом, мы получим 




















 Для доказательства теоремы рассмотрим следующий интеграл
Для доказательства теоремы рассмотрим следующий интеграл
Где


































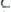








Подынтегральная функция R(x) обладает свойством симметрии, а именно
Асимптотику интеграла несложно вычислить с помощью теоремы Лапласа.

414
Пусть
Найдем нули 









 отличные от нулей g(t). В результате получим,
отличные от нулей g(t). В результате получим,
что
Полученное значение совпадает с результатом наилучшей оценки меры иррациональности. Далее я применяю данный алгоритм для нахождения другого значения меры иррациональностиlog(3), то есть с меньшим
приближением. |
|
Теорема 1: для любого |
существует положительное целое число |
такое что |
|
Таким образом, мы получим 






















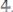 Рассмотрим следующий интеграл:
Рассмотрим следующий интеграл:
Подынтегральная функция R(x) обладает свойством симметрии, а именно
Асимптотику интеграла несложно вычислить с помощью теоремы Лапласа.
Пусть 


















Найдем нули 









 отличные от нулей g(t). В результате получим,
отличные от нулей g(t). В результате получим,
что
Таким образом, мной было получено значение меры иррациональности числа log(3) с использованием алгоритма К. Ву.
Работа выполнена под руководством проф.каф. «Высшая математика» В.Х.Салихова
415
Ю. В. Брекина ИГРЫ И СТРАТЕГИИ С ТОЧКИ ЗРЕНИЯ МАТЕМАТИКИ
Объект исследования: игры и стратегии.
Результаты, полученные лично автором: на примерах рассмотрены различные методы решения игр.
Первые работы по теории игр принадлежат Цермело и Борелю и относятся к началу XX в. В 1928 г. фон Нейман доказал основную теорему теории игр.
Теория игр – совокупность математических методов анализа и оценки конфликтных ситуаций – находит широкое применение к вопросам бизнеса в условиях конкуренции, к планированию военных операций. Установленная связь теории игр и линейного программирования позволяет применять методы решения игр к самым разнообразным задачам управления производством.
Существенная разница между стратегическими играми и играми чисто случайными заключается в том, что в играх первого рода можно использовать мастерство и умственные способности игроков. А во вторых они бесполезны. Такие игры называются играми с природой. Под термином «природа» понимают всю совокупность внешних обстоятельств, в которых сознательному игроку приходится принимать решение. Сознательного игрока называют статистиком. При решении таких игр достаточно найти только оптимальное решение для статистика, так как природа в рекомендациях не нуждается, развиваясь в соответствии с определенными законами независимо от того, удобно это статистику или нет.
Пусть задана платежная матрица игры размерности m x n.
|
|
а |
а |
... |
а |
|
|
|
11 |
12 |
... |
1n |
|
А |
а21 |
а22 |
а2n |
|||
|
|
... |
... |
... |
. |
|
|
... |
|
||||
|
|
аm1 |
аm2 |
... |
|
|
|
|
аmn |
||||
Нижняя цена игры
max min aij .
i 1,...m i 1,...,n
Верхняя цена игры
min max aij .
i 1,...,n i 1,...,m
Если α=β=ν, то число ν называется ценой игры. Если α=β, то игра называется игрой с седловой точкой. Если игра имеет седловую точку, то оптимальное решение игры определяется парой чистых стратегий Аi, Bj, которые соответствуют седловой точке.
Если игра, заданная платежной матрицей, не имеет седловой точки, то для нахождения ее решения используются смешанные стратегии. Пусть SA (p1,p2,...,pm) – смешанная стратегия игрока А. Тогда вероятности
416
p1,p2,...,pm , с которыми игрок А должен чередовать чистые стратегии, определяются из системы уравнений:
а11р1 а21 р2 ... аm1 pm ,
а12 р1 а22 р2 ... аm2 pm ,
...
а1n р1 а2n р2 ... аmn pm ,
|
p1 p2 ... pm 1. |
|
Если SA (q1,q2,...,qn ) – смешанная стратегия игрока В, то вероятности q1,q2,...,qn определяются из следующей системы уравнений:
а11q1 а12q2 ... а1nqn ,
а21q1 а22q2 ... а2nqn ,
...
аm1q1 аm2q2 ... аmnqn ,
|
q1 q2 ... qm 1. |
|
Приведем пример платежной матрицы игры, которая имеет седловую точку.
|
|
5 |
3 |
1 |
20 |
|
|
Пусть дана платежная матрица игры |
|
5 |
5 |
4 |
6 |
|
|
|
. Эта матрица |
||||||
|
|
|
4 |
2 |
0 |
5 |
|
имеет седловую точку 2 |
|
|
|
||||
3 , так как 4 является минимумом второй строки и |
|||||||
максимумом третьего столбца, т.е. 4, |
4. |
Следовательно, при игре, |
|||||
имеющую такую платежную матрицу, оптимальным выбором для первого игрока является 2, для второго – 3. Цена игры равна 4. Выбрав 2, первый игрок может быть уверен, что он получит по меньшей мере 4, а выбрав 3, второй игрок может не допустить, чтобы первый получил более 4.
Работа выполнена под руководством ст. преп. кафедры «Высшая математика» В. А. Андросенко
А.П.Васильев ЦЕПИ МАРКОВА
Исследовано понятие марковской цепи. Рассмотрен пример решения задачи.
Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий Ai из полной группы. События называются состояниями системы, а испытания – изменениями состояний системы.
Рассмотрим пример. Предположим, что речь идет о последовательных бросаниях монеты при игре "в орлянку "; монета бросается в условные моменты времени t = 0, 1, ... и на каждом шаге игрок может выиграть ±1 с

417
одинаковой вероятностью 1/2, таким образом в момент t его суммарный выигрыш есть случайная величина ξ(t) с возможными значениями j = 0, ±1, ...
При условии, что ξ(t) = k, на следующем шаге выигрыш будет уже равен ξ(t+1) = k ± 1, принимая указанные значения j = k ± 1 c одинаковой вероятностью 1/2. Условно можно сказать, что здесь с соответствующей вероятностью происходит переход из состояния ξ(t) = k в состояние ξ(t+1) = k
± 1.
Обобщая этот пример, можно представить себе "систему" со счетным числом возможных "фазовых" состояний, которая с течением дискретного времени t = 0,1,… случайно переходит из состояния в состояние.
Пусть ξ(t) есть ее положение в момент t в результате цепочки случайных переходов: ξ(0) - ξ(1) - ... - ξ(t) - ... ... (1). Обозначим все возможные состояния целыми i = 0, ±1, ... Предположим, что при известном состоянии ξ(t) = k на следующем шаге система переходит в состояние ξ(t+1) = j с условной вероятностью pkj = P(ξ(t+1) = j|ξ(t) = k) , независимо от ее поведения в прошлом, точнее, независимо от цепочки переходов до момента t:
P(ξ(t+1) = j|ξ(0) = i, ..., ξ(t) = k) = P(ξ(t+1) = j|ξ(t) = k) при всех t, k, j ..-
марковское свойство.
Такую вероятностную схему называют однородной цепью Маркова со счетным числом состояний - ее однородность состоит в том, что определенные переходные вероятности pkj, не зависят от времени. Ясно, что Pij - квадратная матрица с неотрицательными элементами и единичными
суммами по строкам. |
|
|
|
|
Такая |
матрица |
(конечная |
или |
бесконечная) |
называется стохастической матрицей, в которой суммы элементов всех строк равны единице.
Равенство Маркова: 


























 .
.
Здесь n– число шагов (испытаний), за которое система перешла из состояния i в состояние j. Зная переходные вероятности, можно найти вероятности перехода из состояния в состояние за два шага Pij(2), т.е. матрицу Р2, зная ее – найти матрицу Р3, и т.д. Эта формула - не что иное как формула перемножения двух матриц.
Пример. Задана матрица переходов 











 . Найти матрицу Р3.\
. Найти матрицу Р3.\
Решение: |
.= |
. |
|
|
. |
Работа выполнена под руководством доц. каф. «Высшая математика» М.Г. Башмаковой.
418
В.С. Гавриков МАТЕМАТИКА И ИСТОРИЯ РАЗВИТИЯ ЧЕЛОВЕЧЕСКОЙ
МЫСЛИ
Объект исследования: отдельные диссертационные работы в области математики 2000-2012г.г. и предопределившие их открытия прошлого.
Результаты, полученные лично автором: изучены существующие диссертационные работы последних лет в области математики, проанализирован исторический материал, являющийся базовым для данных работ, обобщены и систематизированы полученные данные.
Данная работа направлена на выявление связей между диссертационными работами XXI века и предшествующими этим работам открытиями математиков прошлого.
Рассмотрена диссертация по теме «Регуляризация сингулярновозмущенных параболических задач».
Автор: Омуралиев Асан Сыдыгалиевич – доктор физикоматематических наук.
Целью данной работы является изучение краевых задач для сингулярновозмущенных дифференциальных уравнений с частными производными параболического типа, когда предельный оператор не имеет спектр. Отсутствие спектра предельного оператора определенным образом влияет на формирования в решениях новых типов сингулярностей, не поддающихся описанию в терминах спектра предельного оператора. Второй проблемой, изучаемой в данной работе, являются краевые для параболических уравнений с малым параметром при всех производных, когда граница области не является гладкой, а содержит угловые точки.
Начиная с сороковых годов в этом направлении значительный вклад внесли А.Н.Тихонов, Л.С.Понтрягин, Н.Н.Боголюбов, Ю.А.Митропольский, В.П.Маслов, М.И.Вишик, Л.А.Люстерник, А.Б.Васильева, М.И.Иманалиев, С.А.Ломов, В.Ф.Бутузов, К.А.Касымови. Усилиями этих ученых и их учеников созданы различные асимптотические методы решения сингулярновозмущенных уравнений.
В шестидесятых годах прошлого столетия С.А.Ломовым разработан метод, который снимает ограничение на расположение спектра предельного оператора относительно мнимой оси. Асимптотические ряды, получаемые этим методом, являются единственными в определенном классе функций, допускают применение к задачам колебательного и неколебательного типов, при некоторых ограничениях на искомые функции задачи могут сходится не только асимптотически, но и в обычном смысле.
Диссертация по теме «Алгебраическая характеризация классов непрерывных и интегрируемых функций».
Автор: Серединский Александр Александрович – кандидат физикоматематических наук.
Данная диссертация посвящена исследованию колец и решёточноупорядоченных групп непрерывных функций и функций, интегрируемых по
419
Риману. Главной целью работы является чисто алгебраическая характеризация семейства непрерывных функций на компактном пространстве и его классического расширения, составленного из функций, интегрируемых по Риману. Результаты работы относятся к теории функциональных алгебраических систем.
Еще в 1904 году Лебегом и независимо от него Витали была дана знаменитая характеризация функций, интегрируемых по Риману.
Диссертация по теме «Оценка ошибки численных методов для решения дифференциальных уравнений второго порядка».
Автор: Золотарева Наталья Дмитриевна – доктор физикоматематических наук.
Данная работа посвящена получению строгой оценки ошибки численного решения задачи Коши. Задачи вида, где правая часть дифференциального уравнения не зависит от первой производной, встречаются в механике и в квантовой теории рассеяния. Случай, когда задача имеет колеблющееся решение, представляет собой наибольший интерес. Предложенные в работе способы оценки ошибки метода Штермера позволяют одновременно с получением приближенного решения строить его окрестность, содержащую точное решение, то есть указывать границы, в которых заключено точное решение. Для увеличения длины отрезка применимости предложенных методов оценки ошибки предлагается производить вычисления с большим числом значащих цифр и использовать либо меньший шаг, либо метод Штермера более высокого порядка.
Первоначально дифференциальные уравнения возникли из задач механики. К дифференциальным уравнениям приводили также некоторые рассмотренные в то время геометрические задачи. Теория дифференциальных уравнений с частными производными и теория потенциала усиленно разрабатывались в начале и середине XIX века. В этом направлении работало большинство крупных математиков: К.Гаусс, Ж.Фурье, С.Пуассон, О.Коши, П.Дирихле, М.В.Остроградский. В конце XIX в. и в XX в. большое внимание уделяется методам численного интегрирования дифференциальных уравнений.
Представленный материал дает возможность продемонстрировать на занятиях взаимосвязь и преемственность открытий в области математики.
Работа выполнена под руководством ассистента кафедры «Высшая математика» А.А. Семикиной
А.В. Гонский ОЦЕНКА ВЕРОЯТНОСТИ БИНОМИАЛЬНОГО
РАСПРЕДЕЛЕНИЯ ПО ОТНОСИТЕЛЬНОЙ ЧАСТОТЕ
Рассмотрены точечная и интервальная оценки вероятности биномиального распределения.
Решена задача по построению доверительного интервала для вероятности.

420
Пусть производятся независимые испытания с неизвестной
вероятностью р появления события А в |
каждом испытании. |
Требуется |
оценить неизвестную вероятность р по |
относительной частоте, |
т.е. надо |
найти ее точечную и интервальную оценки. |
|
|
1. Точечная оценка. В качестве точечной оценки неизвестной вероятности р принимают относительную частоту W = m/n, где m – число появлений события А; n – число испытаний. Эта оценка несмещенная, т.е. ее математическое ожидание равно оцениваемой вероятности: М (W) = М [m/n] = М (т)/n = nр/n – р.
Найдем дисперсию оценки, приняв во внимание, что D(m) = npq: D (W) = D [m/n] = npq/n2 = pq/n.
2. Интервальная оценка. Найдем доверительный интервал для оценки вероятности по относительной частоте.
Если n достаточно велико и вероятность р не очень близка к нулю и к единице, то можно считать, что относительная частота распределена
приближенно нормально и М (W) = р. |
равенство P(|W – р| < δ) = |
|||
Таким образом имеем |
приближенное |
|||
2Φ(δ/σw). |
|
|
|
|
Построим |
доверительный интервал |
(p1 p2) с |
доверительной |
|
вероятностью γ. |
Так как |
Р (| W – р |< δ) = 2Φ (δ/σ) |
= γ, тозаменив |
|
σw через , получим Р (| W – р |< δ) = 2Φ

 = γ.
= γ.
Таким образом, с надежностью γ выполняется неравенство
Учитывая, что вероятность р неизвестна, решим это неравенство относительно р. Допустим, что w > р. Тогда обе части неравенства положительны; возведя их в квадрат, получим равносильное квадратное
неравенство относительно р:
[(t2/n) + 1)]p2 – 2[w + (t2/n)]p + w2 < 0.
Дискриминант трехчлена положительный, поэтому его корни действительные и различные:
.
Тогда искомый доверительный интервал р1 <р< р2.
Пример. Производят независимые испытания с одинаковой, но неизвестной вероятностью р появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности р с надежностью 0,95, если в 80 испытаниях событие А появилось 16 раз.
Решение. По условию, n = 80, m = 16, γ = 0,95. Найдем относительную частоту появления события А:
w = m/n = 16/80 = 0,2.



 , которую называют логарифмической функцией
, которую называют логарифмической функцией


 достигают максимума при одном и том же
достигают максимума при одном и том же .
.



 отрицательна, то
отрицательна, то

 – точка максимумаи её можно взять в качестве
– точка максимумаи её можно взять в качестве




































































 .
.









































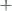




















 ,
,













 .
.








 . В этой точке вторая производная отрицательна, значит это
. В этой точке вторая производная отрицательна, значит это