
Сборник 70 студ конференции БГТУ
.pdf
441
Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Обыкновенное дифференциальное уравнение второго порядка имеет следующий вид:













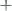






















 .
.
Краевые условия:
где 





















 - заданные функции;
- заданные функции; 


 - заданные числа. Для решения задачи применим метод сеток, заключающийся в аппроксимации первой и второй производных. Учитывая формулы численного дифференцирования, для которых значения производных записываются через значения функций в узлах равномерной сетки с шагом
- заданные числа. Для решения задачи применим метод сеток, заключающийся в аппроксимации первой и второй производных. Учитывая формулы численного дифференцирования, для которых значения производных записываются через значения функций в узлах равномерной сетки с шагом 













 (n - число отрезков разбиения), покрывающей
(n - число отрезков разбиения), покрывающей 



 , а также
, а также
исходя из формул второго порядка, после преобразований имеем:
где

























 .
.
Здесь система записана для внутренних узлов сетки {

 }. Она является трехдиагональной системой линейных алгебраических уравнений и решается методом прогонки.
}. Она является трехдиагональной системой линейных алгебраических уравнений и решается методом прогонки.
Приведенный алгоритм решения краевых задач был реализован в программной среде Mathcad. Сравнительные результаты с аналитическими решениями показали, что расхождения не превышают 5%.
Работа выполнена под руководством доц. кафедры «Высшая математика» А.С. Васильева
Е.Д. Мялкина СИМПЛЕКС – ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
Последовательный симплексный метод планирования (ПСМ) предложен в 1962 г. Он является одним из эффективных методов поиска оптимума. ПСМ относится к безградиентным методам поиска оптимума в факторном пространстве. Он не требует вычисления составляющих градиента / xi , последовательно позволяет определять направление движения и связан с простыми расчетами при шаговом движении к оптимуму. Для каждого шага по методу требуется один опыт. План эксперимента располагается в точках — вершинах симплекса. Симплексом называется правильный выпуклый многогранник, имеющий k+1 вершину в k-

442
мерном факторном пространстве. Для k = 2 правильным симплексом будет равносторонний треугольник с вершинами 1, 2, 3 (рис. 1,а), при k = 3 — тетраэдр с вершинами 1, 2, 3, 4 (рис. 1,б) и т. д. В некоторых модификациях ПСМ приходится иметь дело с неправильными симплексами.
Применение правильных симплексов упрощает процедуру последовательного расчета вершин симплекса и, кроме того, правильный симплекс соответствует ротатабельному планированию первой степени.
Процедура ПСМ для правильного симплекса состоит в выборе начального симплекса и последовательном отражении его вершины с наихудшим откликом в новую точку относительно противоположной грани. Процесс заканчивается при достижении экстремальной области. Для k=2 сущность симплексного метода движения к оптимуму можно проиллюстрировать следующим примером (рис. 2).
Процесс начинается с постановки опытов 1, 2, 3 в вершинах начального симплекса. Начальный симплекс располагают в факторном пространстве на основе априорной информации об объекте исследования. Результаты опытов в вершинах 1, 2 и 3 упорядочивают, т. е. ранжируют по величине отклика. В этомРис.ряду1. Правильныевыбираютдвухнаихудший- и трехмерныерезультатРис.2.ДляПримерповерхностидвижения котоптимумукл ка
y (x ,x ) симплексы. по симплексному методу
1 2 изображенной на рис. 2 с вершинами в точках 1, 2, 3, наихудший опыт будет в точке 1. Для первого шага к оптимуму на грани 2—3, противоположной наихудшему опыту, симметрично строят новый правильный симплекс 2, 3, 4. Причем построение этого симплекса состоит лишь в расчете координат одной точки 4. Затем сравнивают опытные результаты в вершинах полученного симплекса, исключают наихудший из
них и рассчитывают вершину следующего
xH
симплекса — точку 5. Координаты каждой новой вершины симплексов ui рассчитывают по формуле:
~H |
|
2 |
k 1 |
~ |
~* |
~* |
|
|
|||
x |
|
|
|
( x |
x |
|
) x |
|
, |
(1) |
|
|
k |
|
|
||||||||
|
ui |
|
u 1 |
|
ui |
ui |
|
ui |
|
|
|
где k — число факторов: и — номер опыта, т. е. вершины симплекса (и= 1, 2,
...,k+1),i — номер фактора; xui* — координата i-фактора в наихудшем опыте.
Размерность симплекса соответствует размерности рассматриваемого факторного пространства. Увеличение на единицу размерности симплекса
443
требует добавления одного столбца и одной строки в матрице, соответствующих одной новой экспериментальной точке.
Для примера приведем координаты вершин пятимерного симплекса, условия начальной серии опытов при k = 5 (табл. 1). Аналогичным образом рассчитываются условия опытов на симплексе любой k-размерности.
Эксперимент с помощью ПСМ начинается с постановки всех k+1- опытов, к которым на каждом шаге движения к оптимуму добавляется только один опыт. Матрица исходной серии опытов в кодированных переменных xi
(табл.1) позволяет перевести условия опытов в натуральные
~ ~ ~
переменныеxi x0i xixi .
|
|
|
|
|
Таблица 1 |
|
№ опыта |
x1 |
x2 |
x3 |
x4 |
x5 |
|
1 |
0,5 |
0,289 |
0,204 |
0,158 |
0,129 |
|
2 |
-0,5 |
0,289 |
0,204 |
0,158 |
0,129 |
|
3 |
0 |
-0,578 |
0,204 |
0,158 |
0,129 |
|
4 |
0 |
0 |
-0,612 |
0,158 |
0,129 |
|
5 |
0 |
0 |
0 |
-0,632 |
0,129 |
|
6 |
0 |
0 |
0 |
0 |
-0,645 |
|
На любом шаге оптимизации по симплексному методу можно включить в программу новый фактор, добавив всего одну (k+1)точку к точкам, образующим k-мерный симплекс.
При достижении оптимальной области, если отсутствует существенный дрейф оптимума, можно уточнить его положение следующим образом:
сократить размеры симплекса, а при большой ошибке эксперимента дублировать опыты;
применить центральные композиционные планы второго порядка, ядром которых служит симплексный план,— так называемые симплексносуммируемые планы.
Симплексный метод широко используется для поиска оптимума на реальном объекте и по математической модели. Опыт применения ПСМ свидетельствует об эффективности метода, особенно при большом числе факторов.
Работа выполнена под руководством доц. каф «Высшая математика» Н.А. Ольшевской
Полякова Н. В. ФУНКЦИЯ ПОЛЕЗНОСТИ
Объект исследования:функция полезности. Результаты, полученные лично автором:решение практической задачи, используя полученные в результате исследования теоретические знания .

444
При изучении функций нескольких переменных мы встречаемся с различными экономическими функциями, в частности, одной из базовых функций экономической теории – функцией полезности.
По определению функция полезности – формальное выражение зависимости, которая связывает полезность как результат некоторого действия с уровнем (интенсивностью) этого действия. Такова наиболее широкая трактовка, охватывающая представление о функции общественной полезности потребительских благ и услуг, о функции полезности последствий тех или иных решений в исследовании операций и т. п. В самой общей форме функцию полезности можно записать так: u=u(x1, x2,...xn), где x1, x2,...xn- факторы, влияющие на полезность u.
Исследуются разнообразные математические формы функции полезности: одномерные и многомерные, аддитивные, порядковые и количественные, мультипликативные, монотонные и немонотонные, линейные и нелинейные, одночленные и полиномиальные.
Наиболее часто применяемые функции полезности: функция полезности с полным взаимозамещением благ, функция полезности с полным взаимодополнением благ, неоклассическая функция полезности (функция Кобба-Дугласа), функция полезности замещающе-дополняющего типа, квадратичная функция полезности, логарифмическая функция полезности (функция Бернулли) , экспоненциальная функция полезности.
Из математических свойств данной функции выделим одно: она должна иметь положительную первую производную, что говорит о том, что при увеличении объема благ увеличивается и полезность. Выбирая между разными наборами благ, потребитель, очевидно, предпочтет те из них, полезность которых больше. Поэтому функцию полезности иногда также называют функцией предпочтений. Если потребление одного набора возрастает, при том что потребление других продуктов остается неизменным, потребительская оценка первого продукта повышается. Первая частная производная соответствующей функции называется предельной полезностью этого продукта.
Рассмотрим пример: Предпочтения потребителя, приобретающего 10 литров молока и 2 тюбика зубной пасты в месяц, выражаются логарифмической функцией полезности с коэффициентами x01=x02=1, a1=2, a2=1. Потребитель рассуждает о том, что ему полезнее: приобрести дополнительно 1 литр молока или 1 тюбик пасты?
Запишем функцию полезности потребителя: u=2ln(x1-1)+ln(x2-1). Для ответа на вопрос потребителю нужно сравнить предельные полезности молока и пасты при данном объеме потребления этих товаров. Вычислим предельные полезности:
MU1= =
= =2
=2 =
= =
= =0,22
=0,22 , MU2=
, MU2=
= =2
=2 =
= =
= =1
=1 .
.
445
Таким образом, потребителю значительно полезнее приобрести дополнительно тюбик пасты, чем литр молока.
Работа выполнена под руководством асс.каф. «Высшая математика» А. О. Алейниковой
К.Ю. Помогаева
ПРОГРАММНЫЙ МОДУЛЬ КОНТРОЛЯ ЗНАНИЙ СТУДЕНТОВ ПО КУРСУ "ВЫСШАЯ МАТЕМАТИКА"
Объект исследования: программный модуль для оценки знаний студентов.
Результаты, полученные лично автором: разработана тестирующая программа для контроля знаний студентов, разработаны контрольные измерительные материалы по дисциплинам курса .
Современная форма обучения студентов в высших учебных заведения предусматривает много способов контроля полученных знаний. Все они отличаются своей формой и методикой. Перспективным направлением в нынешнее время является такой вид проверки знаний, как тестирование. Оно позволяет быстро и полно оценить результаты освоенных знаний и навыков испытуемого, а также узнать какие разделы курса были изучены не так успешно. Это позволяет сделать методические выводы по дальнейшему совершенствованию преподаванию курса с той целью, чтобы знания студентов становились более крепкими и глубокими.
Целью исследования является разработка тестирующей программы по дисциплинам кафедры "Высшая математика" для контроля знаний студентов. Основные задачи – разработка концепции тестирования, подбор группы вопросов в соответствии с разделами курса, написание программы в среде разработки Visual Studio 2008 на языке программирования C# с использованием в качестве СУБД PostgreSQL, которая будет удовлетворять всем необходимым требованиям.
Итогом работы стало приложение, построенное на базе клиент-серверной топологии, осуществляющая тестирование студентов, обладающая широкими возможностями. В зависимости от роли пользователя доступны функции собственно прохождения определенных тестов, редактирования самой базы тестов, в которой содержатся вопросы и ответы по разделам. Также имеется возможность занесения результатов прохождения тестов в статистическую базу данных с последующим просмотром с целью вынесения оценок. Стоит особенно подчеркнуть, что данная программа является универсальной и её можно использовать и по другим дисциплинам (достаточно лишь внести в базу данных определенные этими дисциплинами вопросы).
Работа выполнена под руководством доц. кафедры «Высшая математика» А.С. Васильева

446
В.О. Прокопова ЭЛЕМЕНТЫ ТЕОРИИ ИГР
Объект исследования: игровые модели.
Результаты, полученные лично автором:построенаплатежная матрица игры, найдена нижняя и верхняя цены игры, показано отсутствие седловой точки.
Игрок 
 записывает одно из двух чисел: 1 или 2, игрок
записывает одно из двух чисел: 1 или 2, игрок  – одно из трех чисел: 1, 2 или 3. Если оба числа одинаковой четности, то
– одно из трех чисел: 1, 2 или 3. Если оба числа одинаковой четности, то 
 выигрывает и выигрыш равен сумме этих чисел, если четность выбранных игроками чисел не совпадает, то
выигрывает и выигрыш равен сумме этих чисел, если четность выбранных игроками чисел не совпадает, то  выигрывает, выигрыш равен сумме этих чисел. Построить платежную матрицу игры, определить верхнюю и нижнюю цены игры и проверить наличие седловой точки.
выигрывает, выигрыш равен сумме этих чисел. Построить платежную матрицу игры, определить верхнюю и нижнюю цены игры и проверить наличие седловой точки.
Решение:
Для начала построим платежную матрицу в общем виде.
Таблица 1
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
… |
… |
… |
… |
… |
|
|
|
… |
|
Для составления платежной матрицы следует проанализировать поведение каждого из игроков. Игрок 
 может записать число 1– обозначим эту стратегию через
может записать число 1– обозначим эту стратегию через 

 или число 2 – стратегия
или число 2 – стратегия


 . Игрок
. Игрок  может записать число 1 – стратегия
может записать число 1 – стратегия
 , либо число 2 – стратегия
, либо число 2 – стратегия

 , либо число 3 – стратегия
, либо число 3 – стратегия

 . Если игрок
. Если игрок 
 запишет число 1, а игрок
запишет число 1, а игрок  выберет число 2, то есть осуществляется пара стратегий (
выберет число 2, то есть осуществляется пара стратегий (





 ), то игрок
), то игрок 
 платит штраф 3, то есть
платит штраф 3, то есть 



 = – 3. Аналогично получаем
= – 3. Аналогично получаем 



 = – 3,
= – 3, 




 = – 5. Очевидно, что стратегии (
= – 5. Очевидно, что стратегии (






 ) и (
) и (





 ) дают игроку
) дают игроку 
 выигрыш 4, то есть
выигрыш 4, то есть 




 =
= 



 = 4. Аналогично –
= 4. Аналогично – 


 = 2. Таким образом, для игры «поиск» размера 2×3 получаем платежную матрицу.
= 2. Таким образом, для игры «поиск» размера 2×3 получаем платежную матрицу.
Рассмотрим игру 2×3 с матрицей 
 и определим наилучшую из стратегий
и определим наилучшую из стратегий 

 ,
, 


 . Выбирая стратегию
. Выбирая стратегию 
 , игрок
, игрок 
 должен рассчитывать, что игрок
должен рассчитывать, что игрок  ответит на нее той из стратегий
ответит на нее той из стратегий  , для которой выигрыш для игрока
, для которой выигрыш для игрока 
 минимален (игрок
минимален (игрок  стремится «навредить» игроку
стремится «навредить» игроку 
 ).
).
При выборе стратегии 

 (первая строка матрицы) минимальный выигрыш равен
(первая строка матрицы) минимальный выигрыш равен 

 = min(2; –3; 4) = – 3 и соответствует стратегии
= min(2; –3; 4) = – 3 и соответствует стратегии 
 игрока
игрока  . При выборе стратегии
. При выборе стратегии 


 (вторая строка матрицы) минимальный выигрыш равен
(вторая строка матрицы) минимальный выигрыш равен 


 = min (– 3; 4; – 5) = – 5, он достигается при стратегии
= min (– 3; 4; – 5) = – 5, он достигается при стратегии 

 .
.

447
Нижняя цена игры α = max (






 ) = max (–3;–5) = – 3 . Таким образом, игрок
) = max (–3;–5) = – 3 . Таким образом, игрок 
 может выбрать стратегию
может выбрать стратегию

 , так как она является максиминной.
, так как она является максиминной.
Выбирая стратегию 
 (столбец 1), игрок
(столбец 1), игрок  понимает, что игрок
понимает, что игрок 
 ответит стратегией
ответит стратегией 

 , чтобы максимизировать свой выигрыш (проигрыш
, чтобы максимизировать свой выигрыш (проигрыш  ). Следовательно, максимальный проигрыш игрока
). Следовательно, максимальный проигрыш игрока  при выборе им стратегии
при выборе им стратегии 

 равен
равен 


 = max (2; – 3) = 2. Аналогично максимальный проигрыш игрока
= max (2; – 3) = 2. Аналогично максимальный проигрыш игрока 
 (выигрыш
(выигрыш 
 ) при выборе им стратегии
) при выборе им стратегии 

 (столбец 2) равен
(столбец 2) равен 


 = max (–3; 4) = 4. То же самое действие выполняется для стратегии
= max (–3; 4) = 4. То же самое действие выполняется для стратегии 

 , то есть
, то есть 


 = max (4; – 5) = 4.
= max (4; – 5) = 4.
Верхняя цена игры  = min (
= min (








 ) = min (2;4;4) = 2. Следовательно, стратегия
) = min (2;4;4) = 2. Следовательно, стратегия 
 игрока
игрока  является минимаксной.
является минимаксной.
Дополнив таблицу 1 строкой 

 и столбцом
и столбцом  , получим таблицу 2. На пересечении дополнительных строки и столбца будем записывать верхнюю и нижнюю цены игр.
, получим таблицу 2. На пересечении дополнительных строки и столбца будем записывать верхнюю и нижнюю цены игр.
Таблица 2
|
|
|
|
|
|
|
|
|
|
2 |
– |
3 |
4 |
– |
3 |
|
– |
3 |
|
4 |
– 5 |
– |
5 |
|
|
2 |
|
4 |
4 |
= 2 |
= – 5 |
|
|
|
|
||||
|
|
|
|
|
|
|
Пара чистых стратегий 

 и
и
 дает оптимальное решение игры тогда и только тогда, когда соответствующий ей элемент
дает оптимальное решение игры тогда и только тогда, когда соответствующий ей элемент 


 является одновременно наибольшим в своем столбце и наименьшим в своей строке. Так как в данной задаче это условие не соблюдается, то, можно сказать, что седловая точка отсутствует.
является одновременно наибольшим в своем столбце и наименьшим в своей строке. Так как в данной задаче это условие не соблюдается, то, можно сказать, что седловая точка отсутствует.
Так как седловая точка отсутствует нужно найти решение задачи в смешанных стратегиях. Для игрока 
 средний выигрыш равен цене игры
средний выигрыш равен цене игры 
 (при
(при 
 и
и 

 ), для игрока
), для игрока  средний проигрыш равен цене игры
средний проигрыш равен цене игры 
 (при
(при 

 и
и



 ). Системы уравнений в данном случае имеют вид.
). Системы уравнений в данном случае имеют вид.
Данные системы неравенств решений не имеют.
Работа выполнена под руководством ст. преп. каф. «Высшая математика» В.М. Кобзева


449
воспользовавшись общей формулой Даламбера, получим выражения для напряжения и для тока:
u x,t |
f x at f x at |
|
|
|
|
|
L |
|
|
x at x at |
, (6) |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
x at x at |
|
|
|
|
|
|
|
|
|
f x at f x at |
|
|
|
|
|||||||||||||||||||||||||||||||||
i x,t |
|
C |
|
. (7) |
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Линией без искажения называется линия, параметры которой связаны |
||||||||||||||||||||||||||||||||||||||||||||||||
соотношениемRC LG. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В этом случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
R |
t f x at f x at |
|
|
|
|
|
|
|
|
|
|
x at x at |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
u x,t e L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(8) |
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
R |
t x at x at |
|
|
|
|
|
|
f x at f x at |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
C |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
i x,t e L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(9) |
|
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Таким образом, в линии без искажений, так же как в линии без потерь, |
||||||||||||||||||||||||||||||||||||||||||||||||
между напряжением и |
током в прямой и |
обратной |
|
волнах сохраняется |
||||||||||||||||||||||||||||||||||||||||||||
постоянное отношение |
|
L |
(волновое сопротивление). Волны напряжения и |
|||||||||||||||||||||||||||||||||||||||||||||
|
C |
|
||||||||||||||||||||||||||||||||||||||||||||||
тока распространяются, |
|
как |
в |
|
линии |
без потерь, |
но |
|
стой |
существенной |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
t |
|
|
|
|
|
|
|
|
разницей, что |
благодаря множителю |
e L |
обе волны |
со |
временем по |
|||||||||||||||||||||||||||||||||||||||||||
показательному закону затухают. Причиной затухания волн является рассеяние энергии, вызванное выделением тепла в проводах.
Работа выполнена под руководством доц. кафедры “Высшая математика” Г.Г.Цуленевой
Ю.В. Шестеров О КОРРЕКТНОСТИ ЧИСЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ
Объект исследования: погрешность численного дифференцирования Результаты, полученные автором: получение формул численного
дифференцирования для производных различных порядков с учетом погрешности.
Под численным дифференцированием понимаются способы нахождения производной таблично заданной или трудно дифференцируемой аналитически функции. В основе численного дифференцирования лежит аппроксимация функции, от которой берётся производная, интерполяционным методом.
Один из универсальных способов построения формул численного дифференцирования состоит в том, что по значениям функции f(x) в некоторых узлах 















 строят интерполяционный полином
строят интерполяционный полином 






 и
и
приближенно полагают 










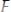















 .
.


 LC
LC 






 (три узла):
(три узла):
















































 ,
,


























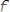








 ,
,




















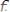
























 ;
;


 ,
,






 ,
,

































 ;
;















































 ,
,






































 ,
,















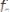











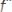











 ,
,



















































 ;
;

 , где
, где 



 , а неустранимая погрешность растет.
, а неустранимая погрешность растет. 



 .
.