2. Растворы сильных электролитов. Активность электролитов

Согласно теории Аррениуса в любых растворах электролитов происходит электролитическая диссоциация, необходимым условием которой является наличие в растворяемом веществе ионных или полярных связей, а также достаточная полярность самого растворителя, которая оценивается величиной диэлектрической проницаемости . Вода имеет высокую диэлектрическую проницаемость (=81), что делает ее сильным ионизирующим растворителем.

Количественно процесс электролитической диссоциации оценивается двумя величинами: степенью диссоциации и константой диссоциацииK_д.

Степенью диссоциации называют долю диссоциированных на ионы молекул. Степень диссоциации зависит от природы растворенного вещества и от концентрации раствора, увеличиваясь с его разбавлением. По значению для растворов молярной концентрации эквивалента 0,1 моль/л электролиты условно делят на три группы: сильные (>30%), средние (=3–30%) и слабые (<3%).

Экспериментально определяемая степень диссоциации сильных электролитов оказывается меньше истинной, поэтому ее называют кажущейся. Заниженность результатов измерений объясняется уменьшением подвижности ионов из-за наличия вокруг каждого из них ионной атмосферы, образованной противоположно заряженными ионами. Такая частичная связанность ионов как бы снижает их концентрацию, а некоторая фиктивная концентрация, определяющая свойства раствора, называется активной концентрацией или просто активностью а. Численно активность равна истинной, аналитически определяемой концентрации, умноженной на коэффициент активности.

В теории сильных электролитов приняты два способа определения активности (и коэффициента активности):

(2.1)

где и– разные обозначения моляльной концентрации электролита, моль/1000 г растворителя;

(2.2)

где – молярность раствора, моль/л.

Коэффициенты активности иfопределяют степень отклонения реальных растворов электролитов от поведения идеальных растворов, что зависит от энергии электростатического взаимодействия заряженных частиц (ионов) в растворе. Для бесконечно разбавленных растворов эта энергия практически равна нулю и поэтому

Это обстоятельство позволяет установить соотношение между определенными разными способами коэффициентами активности.

Возьмем 1 л раствора с концентрацией , моль/л. Тогда моляльность этого раствора

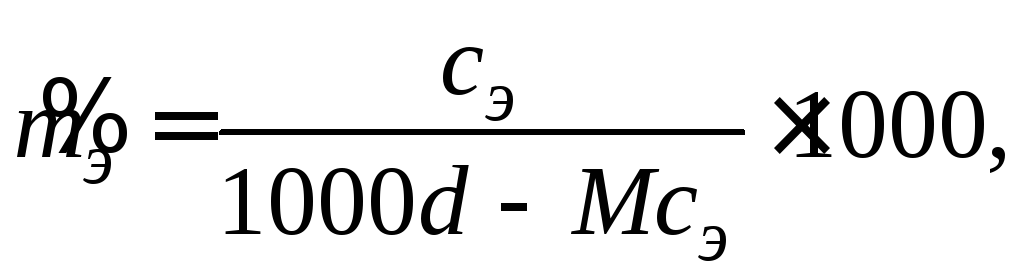(2.3)

где d– плотность раствора, г/см³;M– молярная масса электролита, г/моль. После простых преобразований уравнения (2.3) получим соотношение

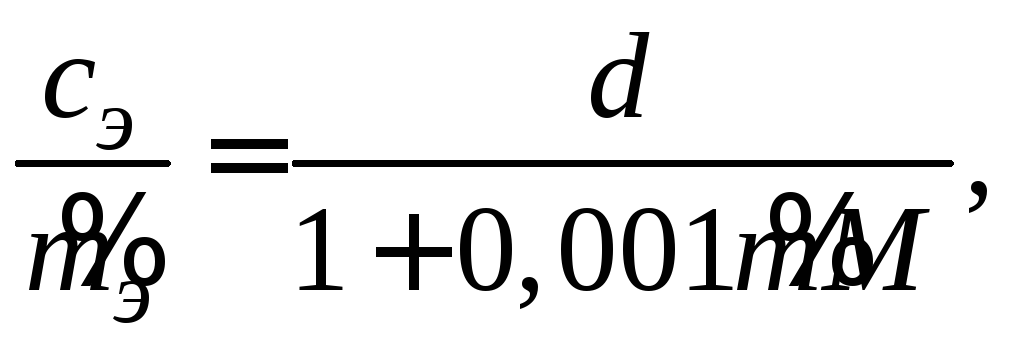(2.4)

из которого следует, что лишь для разбавленных растворов это соотношение

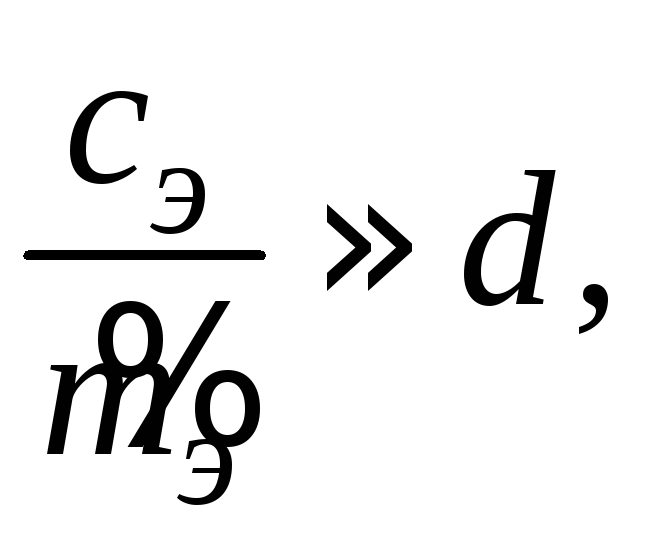
а для бесконечно разбавленных растворов (dd_o)

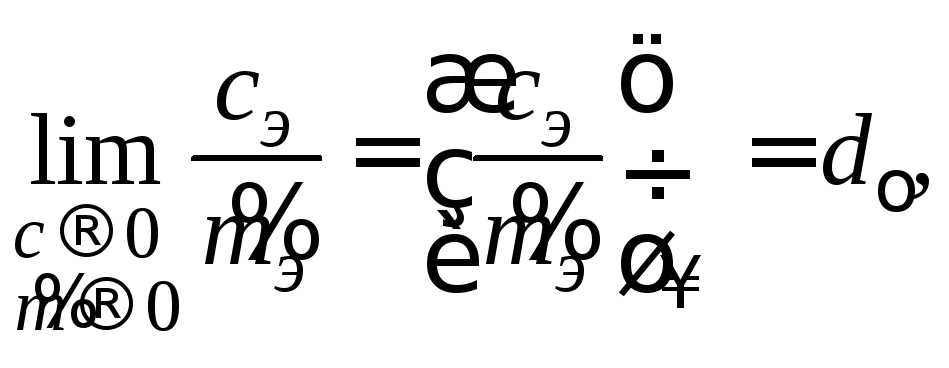
где – плотность растворителя (для воды=1 г/см³). Отношение активностей, определенных относительно разных стандартных состояний, есть величина постоянная, независящая от концентрации. Поэтому

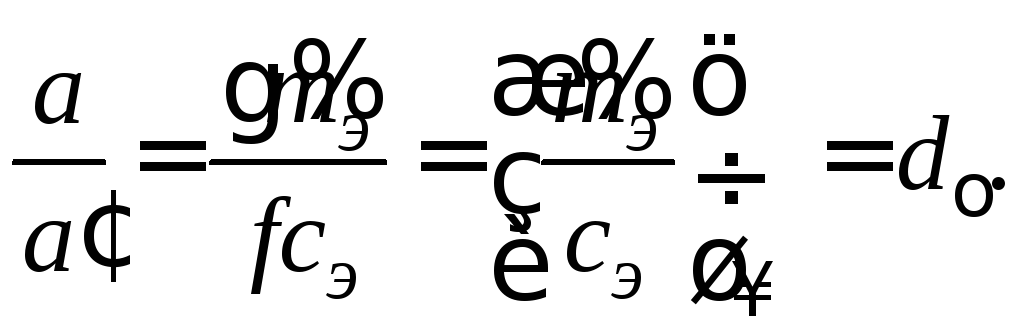(2.5)

Отсюда следует

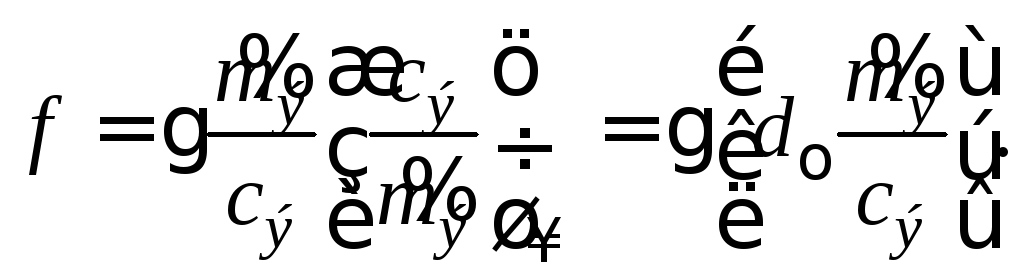
После подстановки в последнее уравнение величины из формулы (2.4) получаем

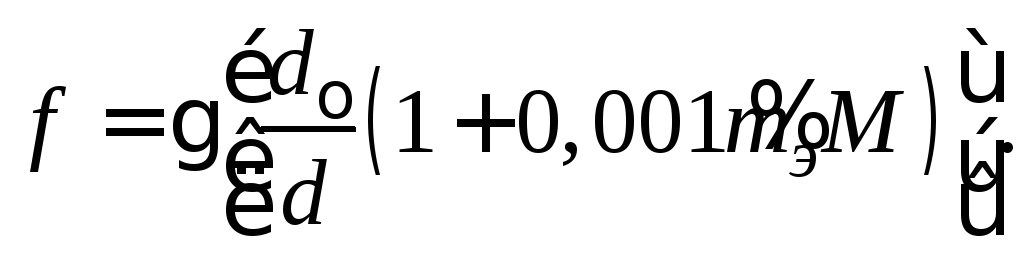(2.6)

В этой формуле выражение в квадратных скобках мало отличается от единицы, поэтому в приближенных практических расчетах даже концентрированных растворов часто коэффициенты активности считаются равными. Поэтому активности, определяемые формулами (2.1) и (2.2), отличаются размерностями, а различие их численных значений определяется различиями молярности и моляльности раствора. В справочной литературе, тем не менее, приводятся величины коэффициентов активности . Это определяется тем обстоятельством, что, строго говоря, свойства любых растворов следует определять в зависимости от соотношения числа частиц компонентов.

Активность электролита можно выразить через активности ионов, используя условие ионного равновесия

(2.7)

Активности ионов

(частный случай),

(частный случай). (2.8)

Однако, определить активности (коэффициенты активности) ионов опытным путем невозможно, поэтому введены понятия среднего ионного стехиометрического коэффициента , средних ионного коэффициента активностии активности, которые и определяются экспериментально. Между этими величинами и характеристиками ионов существуют следующие соотношения:

(2.9)

где определяет число ионов, образующихся при диссоциации молекулы электролита. Из соотношений (2.7)–(2.9) следует

(2.10)

Например, для водного раствора NaCl

для водного раствора CaCl₂

В многокомпонентных растворах активности ионов зависят не только от их концентраций, но и от концентраций других ионов, присутствующих в растворе. Суммарное влияние ионов на активность каждого из них в растворе выражается с помощью ионной силы раствора, которая является мерой электростатического взаимодействия между всеми ионами, находящимися в растворе. Ионная сила раствора Iравна полусумме произведений концентрации каждого иона данного раствора на квадрат его заряда:

(2.11)

Для бинарных растворов ионная сила раствора связана с концентрацией электролита простыми соотношениями, приведенными в табл. 2.1.

Таблица 2.1

Ионные силы бинарных растворов

Тип электролита	Ионная сила (=1)
К+А–(NaCl, NaNO3, HCl)
К2+А2–(CuSO4,ZnSO4)
(BaCl2, Mg(NO3)2) (K2SO4, K2CrO4)
(Na3PO4, H3PO4) (Al(NO3)3, CrCl3)
(Al2(SO4)3)

Эту таблицу можно использовать при вычислениях ионной силы многокомпонентного раствора, считая ее аддитивной. Например, ионную силу раствора, содержащего 0,005 моль/л CuSO₄и 0,01 моль/л Al(NO₃)₃в предположении полной диссоциации солей (=1)

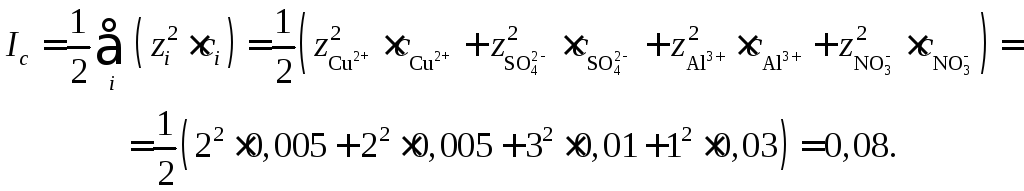
Используя таблицу, получим:

Для растворов электролитов с ионной силой I<0,02 коэффициенты активности ионов можно определить по уравнению Дебая и Гюккеля

(2.12)

С учетом соотношений (2.9) из уравнений (2.12) можно получить формулы для расчета средних коэффициентов активности

(2.13)

Постоянный множитель Азависит от температуры и природы растворителя. Для воды при 25СА=0,509.

Значения коэффициентов активности ионов в зависимости от величины ионной силы раствора приведены в табл. 2.2.

Таблица 2.2

Коэффициенты активности ионов в водных растворах в зависимости от ионной силы раствора и заряда иона

Заряд иона z	Ионная сила раствора, I
	0,0001	0,001	0,002	0,005	0,01	0,02	0,05	0,1	0,2	0,5
1	0,988	0,96	0,95	0,92	0,89	0,87	0,81	0,78	0,70	0,62
2	0,954	0,86	0,81	0,72	0,63	0,57	0,44	0,33	0,24	—
3	0,900	0,73	0,64	0,51	0,39	0,28	0,15	0,08	0,04	—
4	0,830	0,56	0,45	0,30	0,19	0,12	0,04	0,01	0,003	—

В разбавленных водных растворах электролитов, когда ионная сила , коэффициент активности ионов принимается равным единице иили.