10.1. Примеры решения задач

Пример 51. Рассчитать удельный расход активных веществ при работе марганцово-цинкового гальванического элемента.

Решение

Расход активных веществ определяется количеством электричества, взятого от ХИТ. Поэтому на практике рассчитывают расход удельный – в граммах на 1 А·час. Закон Фарадея (см. уравнения (9.1) и (9.2))

для удельного расхода запишем

,

где число Фарадея F= 26,8 А·ч;– эквивалентная масса.

Суммарный процесс, протекающий в марганцово-цинкового гальванического элемента представлен уравнением (10.18)

,

которое, как следует из уравнений (10.8) и (10.10), записано на 4 Фарадея электричества (4 электрона). Поэтомуи, а удельные расходы активных веществ

;

;

.

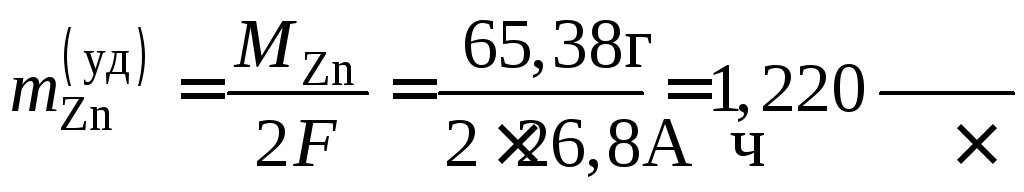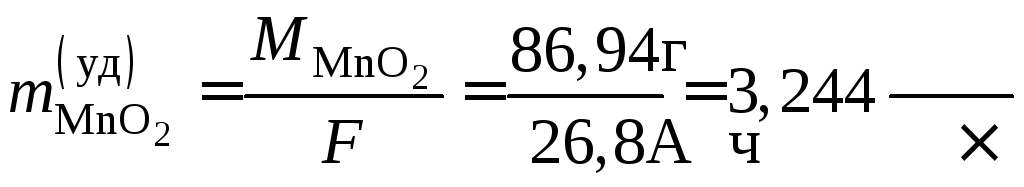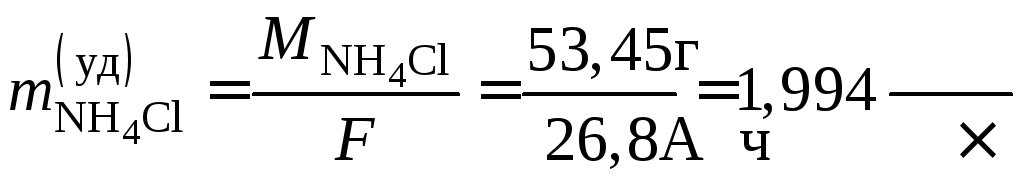Пример 52. Рассчитать стандартный потенциал электродапри 15 °С, если температурный коэффициент стандартного потенциала

.

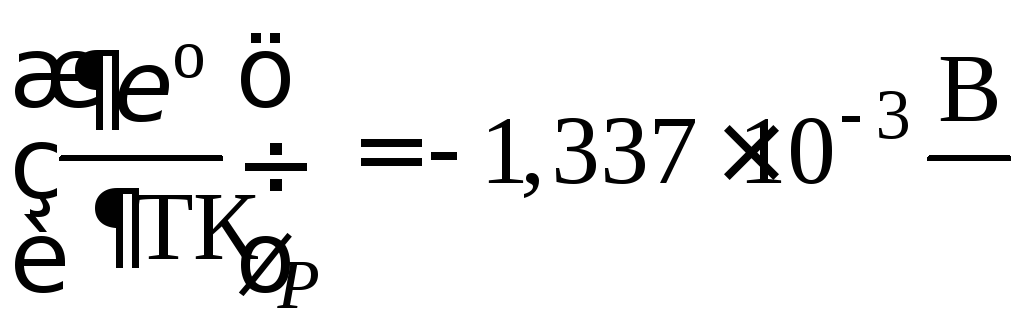Вычислить ЭДС термогальванической системы таких электродов при разнице их температур 10 и 20 градусов.

Решение

Электродная реакция на рассматриваемом электроде и стандартный электродный потенциал при температуре 25 °С (298 К) по справочным данным таковы:

,= +0,345 В.

Стандартный потенциал электрода при температуре Т, отличающейся от стандартной, уравнение (10.25)

,

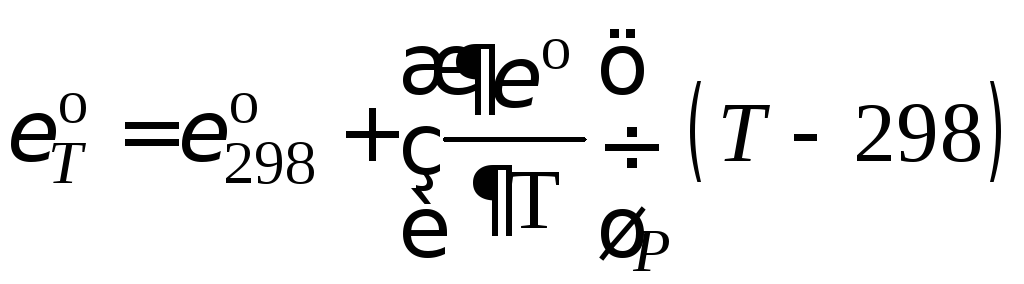поэтому при 15 °С

В.

Термогальванической системой называется гальванический элемент (в общем случае любой ХИТ), составленный из одинаковых электродов, температуры которых разные. В нашем случае это такой гальванический элемент:

.

Электродвижущая сила элемента

,

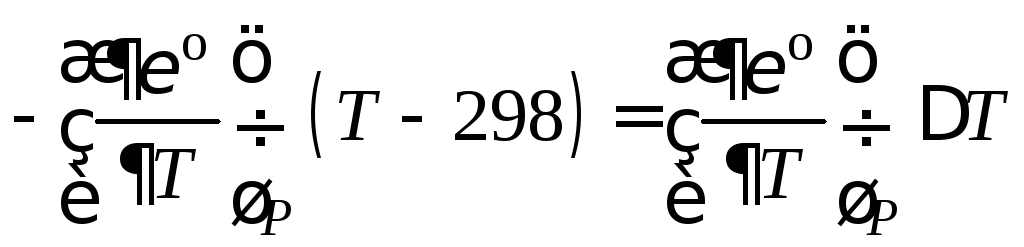поэтому при разнице температур = 10 °

В,

а при разнице = 20 °

В.

Знак минус означает, что потенциал «горячего» электрода меньше, чем «холодного» электрода. Другими словами «горячий» электрод является анодом и на нем протекает процесс

,

а «холодный» – катодом с процессом

.

Пример 53. Вычислить константу равновесия потенциалобразующей реакции в элементе Даниэля при стандартной температуре.

Решение

Элемент Даниэля

с электродными процессами и потенциалобразующей реакцией

,= –0,763 В;

,= +0,337 В;

,.

По уравнению (10.30) имеем

.

Отсюда константа равновесия . Такая огромная величина константы равновесия означает, что, например, равновесие реакции взаимодействия металлического цинка с водным раствором

сильно сдвинуто вправо, другими словами реакция идет до конца (полного расходования одного из исходных реагентов).

Пример 54. Потенциалобразующая реакция гальванического элемента Вестона

.

Определить электродные реакции, условные записи электродов и гальванического элемента. Написать уравнения Нернста для электродных потенциалов и ЭДС элемента. Вычислить изменения энергии Гиббса, энтальпии и энтропии для потенциалобразующей реакции для температуры 35 °С. Известно, что для элемента Вестона температурный коэффициент равен –4,06·10^–5В/К.

Решение

Согласно уравнению реакции активными веществами элемента являются металлический кадмий Cd, ртутьHgи труднорастворимая соль, произведение растворимости= 6,4·10^–7(моль/л)³. Электролитом является водный раствор соли. Один из электродов поэтому является

,

стандартный электродный потенциал которого при 25 °С по справочным данным = –0,403 В. Другой, ртутно-сульфатный электрод

имеет стандартный потенциал . Поэтому на электродах элемента Вестона протекают:

анодная реакция ,

катодная реакция .

Условная запись гальванического элемента Вестона

.

По уравнению Нернста электродные потенциалы анода и катода

,

,

а электродвижущая сила элемента

.

Электродные потенциалы и ЭДС зависят от температуры и концентрации электролита. При температуре 35 °С (308 К) ЭДС элемента Вестона, если

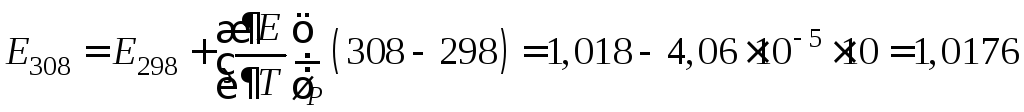В.

Тогда изменение энергии Гиббса для потенциалобразующей реакции элемента Вестона

.

Из уравнения (10.32) находим тепловой эффект реакции

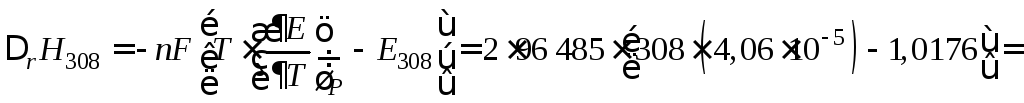= –198 760 Дж или –198,8 кДж.

Изменение энтропии вычисляем по уравнению (10.33)

.

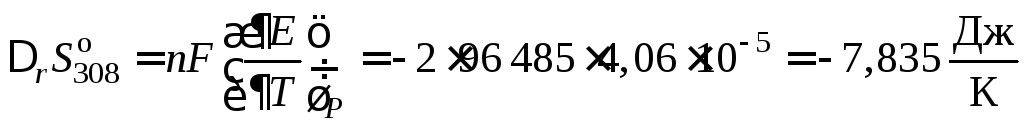Пример 55. Тепловой эффект реакции при 298 К

,= –94 200 Дж.

В каком гальваническом элементе протекает эта реакция? Рассчитайте ЭДС элемента, если экспериментально определенное повышение ее при нагревании равно 1,45·10^–4В/К.

Решение

Из уравнения (10.33) следует

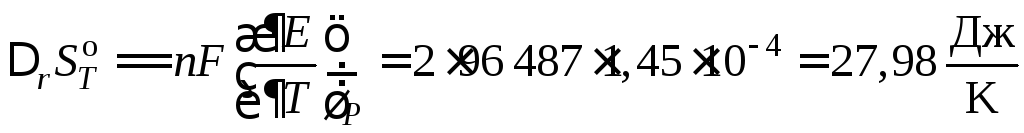
гальванический элемент состоит из свинцового и каломельного электродов

Анодная реакция .

Катодная реакция .

Суммарная реакция ,

изменение энергии Гиббса для которой

.

Следовательно,

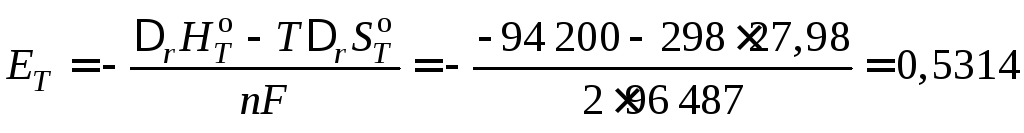В.

Пример 56. В гальваническом элементе

цинковый и хлорсеребряный электроды находятся в одном электролите – водном растворе хлорида цинка с концентрацией соли 0,005 моль/л и средним коэффициентом активности = 0,789. Температура 298 К. Вычислить ЭДС элемента, если стандартные электродные потенциалы= –0,763 В,= +0,222 В.

Решение

Анодный процесс , катодный процесс, поэтому ЭДС элемента

.

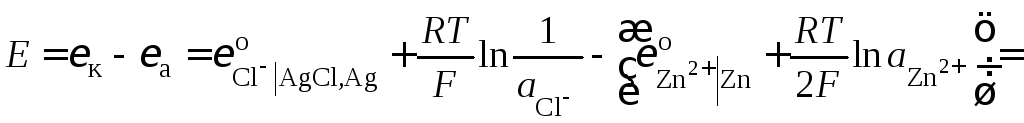
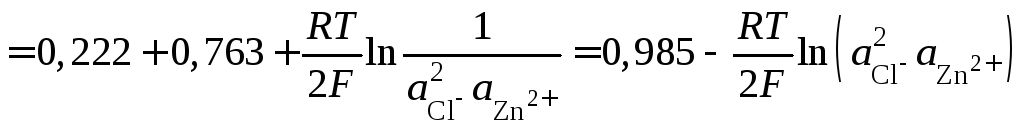Так как средняя активность электролита

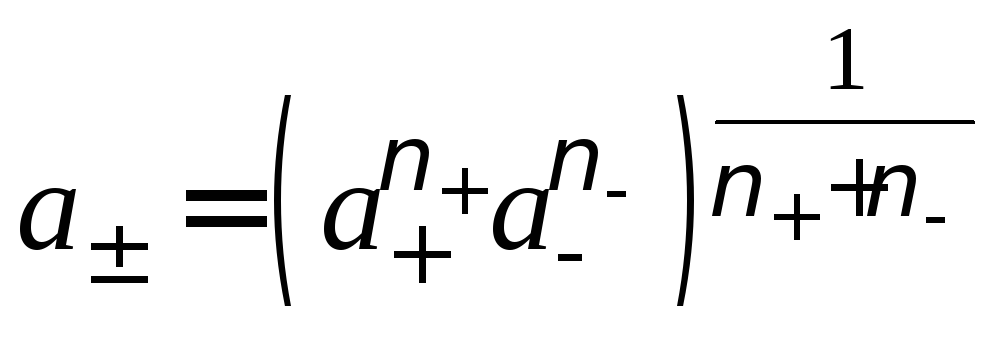, то.

С другой стороны

,,

поэтому для нашего электролита получим

,.

Таким образом,

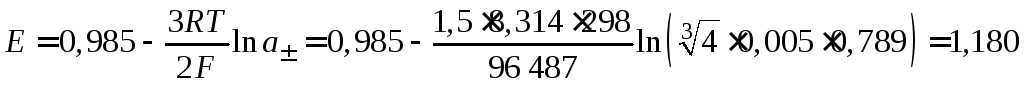В.

Пример 57. При температуре 298 К ЭДС элемента

равна 0,624 В. Определить средний коэффициент активности .

Решение

Электродный потенциал катода (в нашем случае электрода первого рода ) определяется уравнением

.

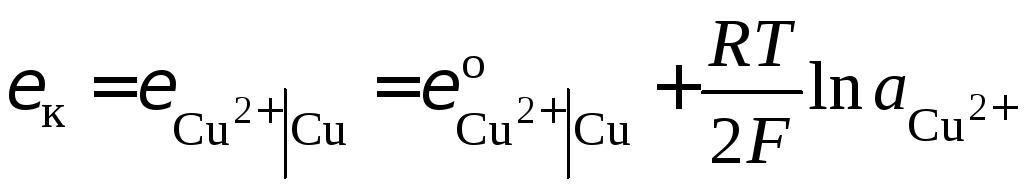Электродный потенциал анода (в нашем случае электрода второго рода ):

.

С учетом табличных значений стандартных электродных потенциалов = 0,3391 В,= –0,3603 В получим

В.

Отсюда

.

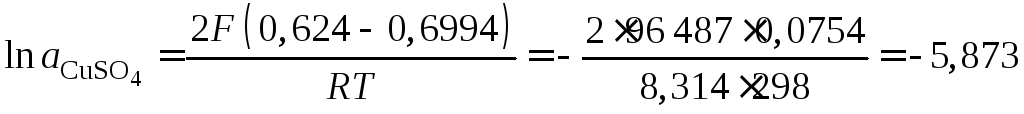Следовательно

,

а коэффициент активности электролита

.

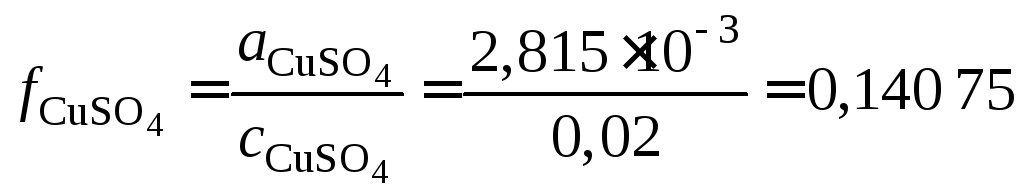Тогда средний коэффициент активности

.