1.1. Примеры решения задач

Пример 1. Вычислить при 20С осмотическое давление водного раствора, в 6 л которого содержится 62,4 г кристаллогидратаCuSO₄5H₂O. Кажущаяся степень диссоциации соли в растворе равна 40%.

Решение

Односторонняя диффузия молекул растворителя через полупроницаемую перегородку (ППП) называется осмосом (рис. 1). Полупроницаемая перегородка обладает свойством пропускать только молекулы растворителя. Осмос впервые обнаружил и наблюдал в эксперименте французский химик Ж. Ноле (1748 г.), впервые измерил немецкий физиолог В. Пфеффер (1877 г.), а уравнение

(1.12)

для растворов неэлектролитов получено Я. Вант-Гоффом в 1886 году. Позднее получено точное уравнение для осмотического давления

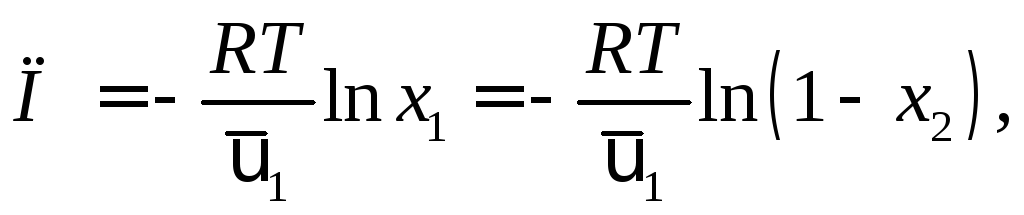(1.13)

где x₂– молярная доля растворенного вещества;– парциальный молярный объем растворителя в равновесном растворе. Уравнение (1.13) преобразуется в формулу Вант-Гоффа для разбавленных растворов.

Рис. 1. Диффузионные потоки при убранной перегородке и через полупроницаемую перегородку

В рассматриваемом растворе концентрация электролита

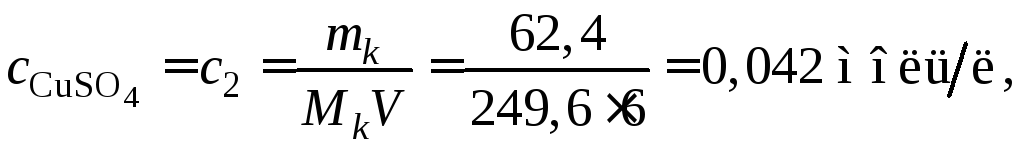
так как одна молекула кристаллогидрата содержит одну молекулу безводной соли CuSO₄. Здесьm_kиM_k– масса и молекулярная масса кристаллогидрата;V– объем раствора. Изотонический коэффициент

Тогда осмотическое давление

Рис. 2. Схема, иллюстрирующая появления осмотического давления:

1 – чистый растворитель; с₂– равновесная концентрация растворенного вещества

Пример 2. Давление пара над раствором, содержащим 67 г солиCa(NO₃)₂в 1000 г воды, при 100С равно 747 мм рт.ст. При какой температуре этот раствор закипит под нормальным давлением? Рассчитать нормальную температуру замерзания раствора. Какова кажущаяся степень диссоциации соли? Эбулиоскопическая и криоскопическая константы воды 0,52 и 1,86 Ккг/моль.

Решение

При 100 С упругость паров чистой воды 760 мм рт.ст., поэтому из закона Рауля (1.8) следует (молекулярная масса солиM₂=164,1 г/моль)

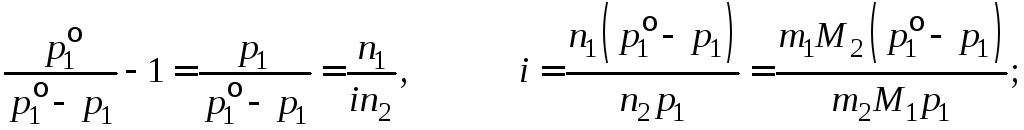
Для азотнокислого кальция Ca(NO₃)₂число ионов, получающихся при диссоциации молекулы,=3. Поэтому степень диссоциации этого электролита при 100С по уравнению (1.7)

или 68,4%.

Нормальные температуры кипения раствора и замерзания из-за отсутствия информации о влиянии температуры на степень диссоциации могут быть вычислены с некоторой ошибкой. Эта ошибка весьма мала для температуры кипения, но может быть заметной для температуры замерзания. Получим согласно формулам (1.9) и (1.10)

Пример 3. Пользуясь табличными данными, вычислить при температуре 25С степень диссоциации цианистоводородной кислотыHCN(цианистый водород, синильная кислота) и концентрации образующихся при диссоциации ионов в 0,001 М растворе.

Решение

Согласно справочным данным (см. табл. приложения) константа диссоциации HCNравна при 25С 7,210^10моль/л. Кислота является бинарным одно-однозарядным электролитом,

поэтому

Так как синильная кислота слабый электролит (<<1), то степень диссоциации величина небольшая (<<1) даже в разбавленных растворах. Поэтому

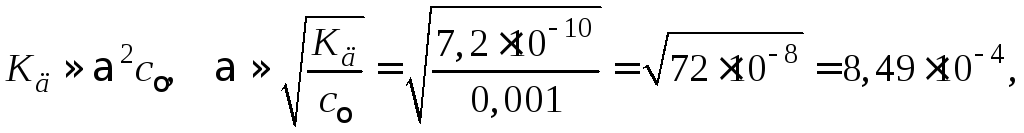
то есть степень диссоциации меньше 0,1% (0,0849%). Концентрация образующихся при диссоциации ионов

Замечания.

1. Точное решение квадратного уравнения

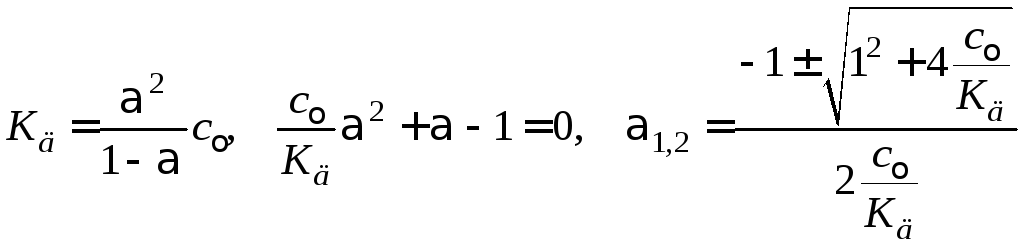(1.14)

с учетом того, что отрицательное значение корня не имеет физического смысла, приводит к результату

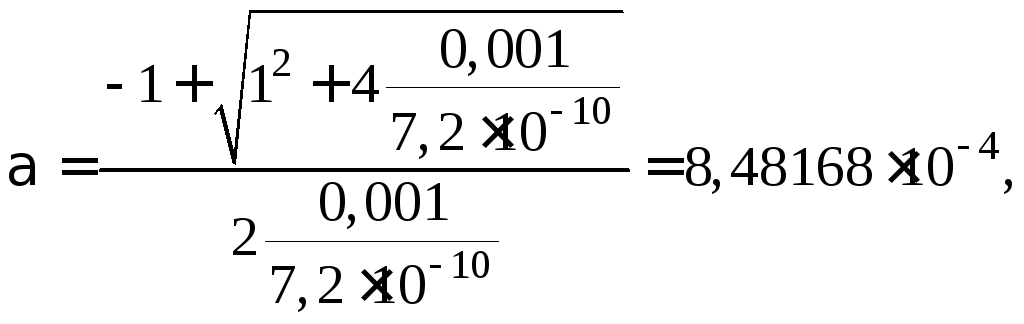
Расхождение этой цифры с величиной, полученной по приближенному уравнению

весьма незначительно и оправдывает использование такого приближенного уравнения.

2. Как видно из уравнения

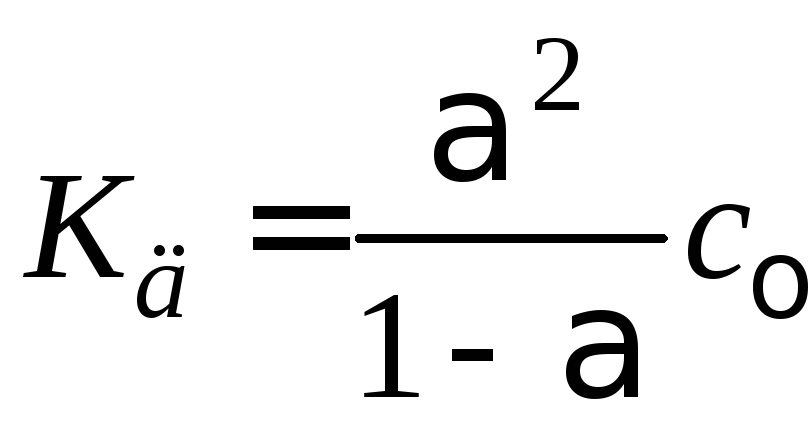
степень диссоциации при заданной температуре зависит от концентрации раствора и, согласно закону разбавления Оствальда, для любых электролитов при , то есть для сильно разбавленных растворов для слабых электролитов нельзя пользоваться приближенным уравнением. Поэтому возможность использования приближенного уравнения рекомендуется оценивать по неравенству, см. уравнение (1.14). В нашем примере это неравенство выполняется:

Пример 4. Рассчитать степень диссоциации уксусной кислотыCH₃COOHи концентрацию ионов водорода в растворе с концентрацией 0,005 моль/л. Как изменится степень диссоциации кислоты и концентрация ионов водорода, если к 3 литрам такого раствора добавить 9 г уксуснокислого натрияCH₃COONa? Соль считать полностью диссоциированной. Температура 25С.

Решение

Для бинарного раствора H₂O–CH₃COOHпроцесс диссоциации

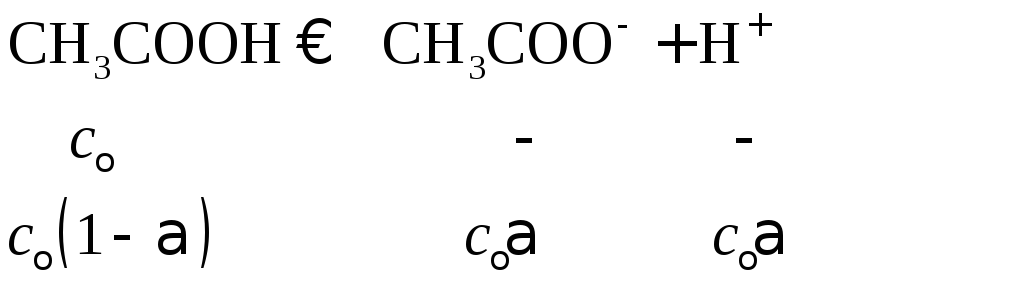
описывается уравнением

По справочным данным (см. приложение) для уксусной кислоты . Так как отношение (см. пример 3)

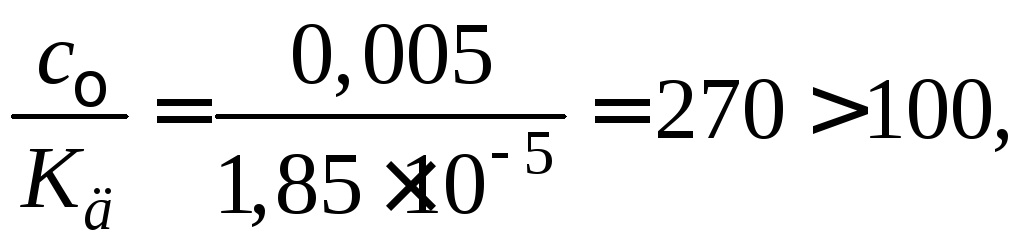
можно степень диссоциации рассчитать по приближенному уравнению

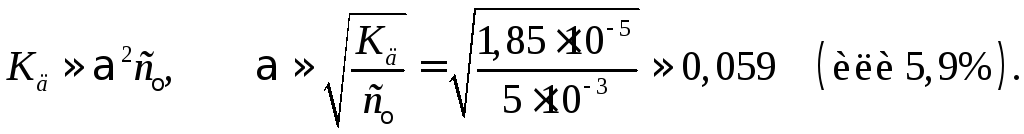
Тогда концентрация ионов водорода в бинарном растворе

В тройном растворе H₂O–CH₃COOH–CH₃COONaконцентрация соли

поэтому с учетом полной диссоциации «вклад» соли в общую концентрацию анионов CH₃COO^–составляет

Процесс диссоциации кислоты в тройном растворе

описывается уравнением

(1.15)

Точное решение квадратичного уравнения

дает для степени диссоциации кислоты в тройном растворе

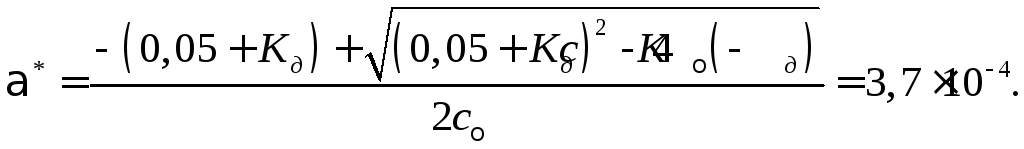
Концентрация ионов водорода в тройном растворе

Таким образом, степень диссоциации кислоты и концентрация ионов водорода в тройном растворе уменьшились в 160 раз

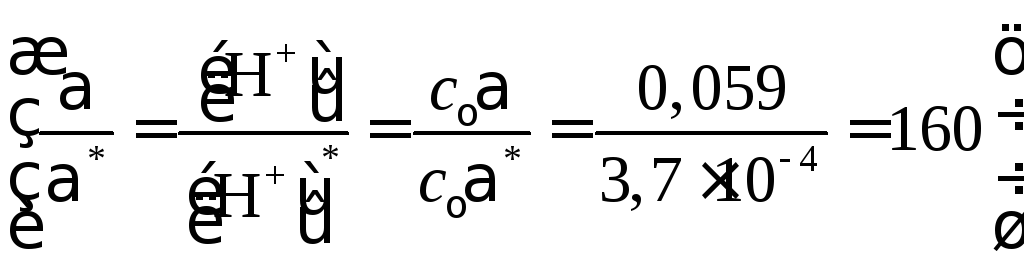
по сравнению с бинарным раствором.

Замечание. Если учесть, что в уравнении (1.15)и^*<<1, можно вместо точного расчета вычислить^*по приближенному уравнению

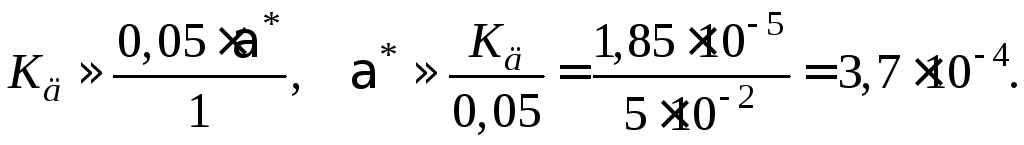
Пример 5. Рассчитать концентрацию ионовив водном растворе фосфорной кислотыH₃PO₄с концентрацией 0,1 моль/л при 25С.

Решение

По справочным данным ступенчатая диссоциация фосфорной кислоты описывается следующими уравнениями и константами диссоциации:

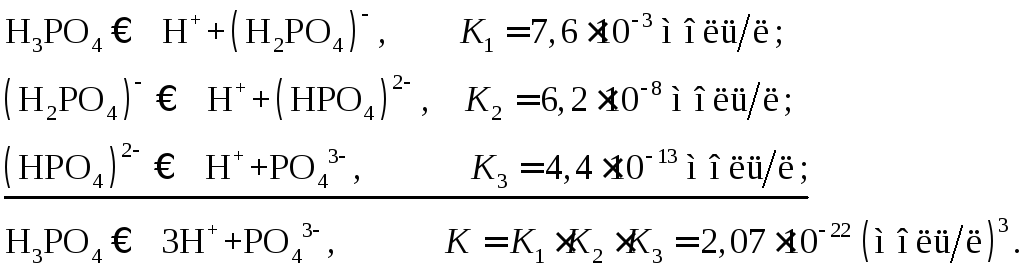
Концентрация ионов водорода в растворе определяется «вкладами» каждой ступени диссоциации

но из-за большой разницы констант диссоциации

можно считать . Поэтому получим

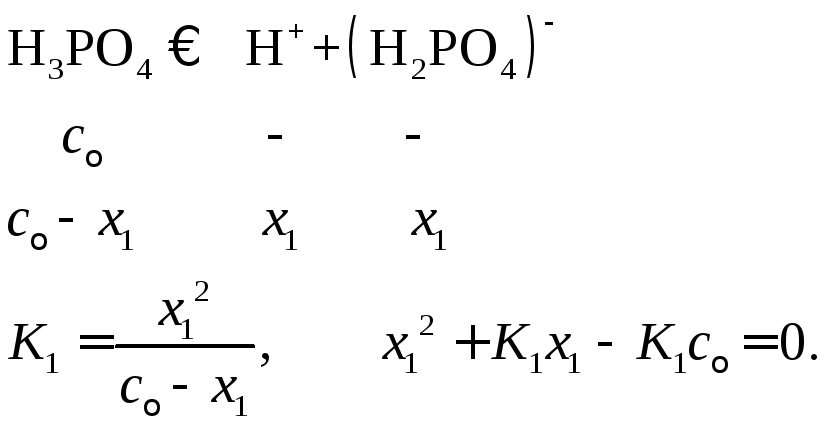
Здесь x– числа молей ионов, образующихся при диссоциации, в расчете на 1 литр раствора. Так как в рассматриваемом примере

необходимо решать квадратное уравнение

Получим

Для определения концентрации ионов необходимо решить систему трех уравнений (с учетомx₂<<x₁,x₃<<x₂):

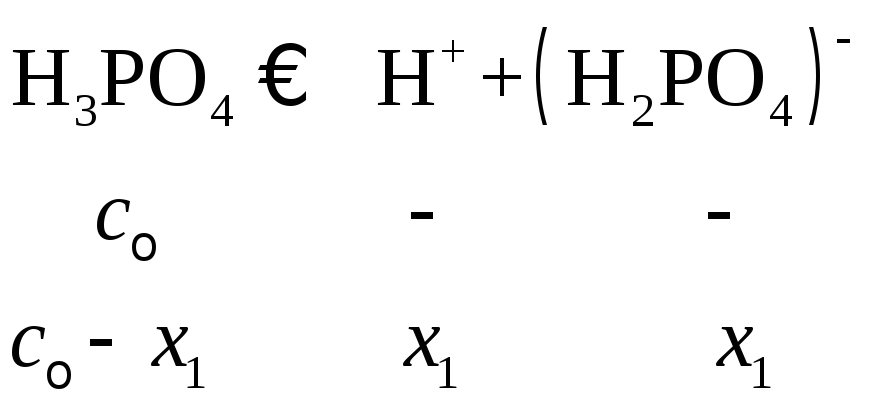
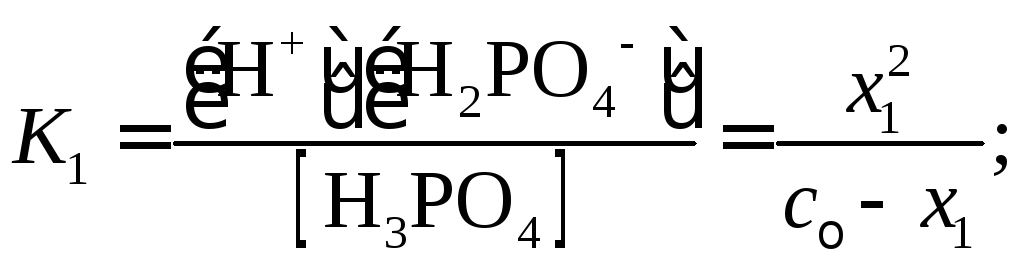
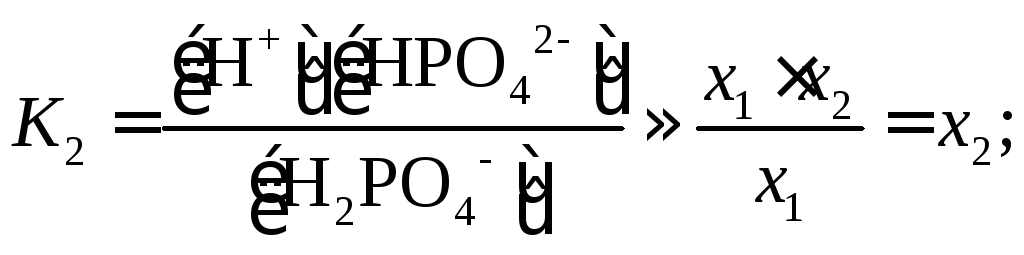
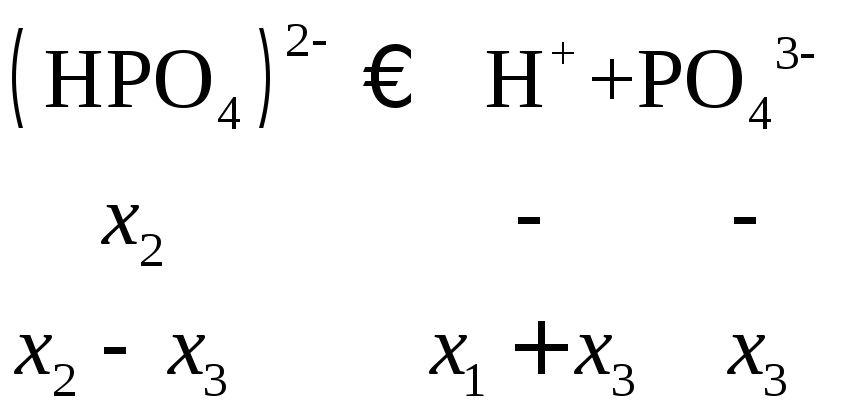
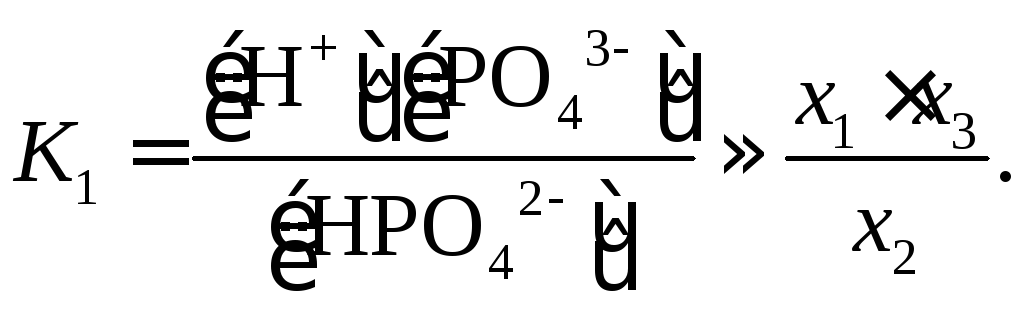
Величина x₁нами уже вычислена:x₁=2,410^–2. Величинаx₂K₂=6,210^–8моль/л. Наконец,

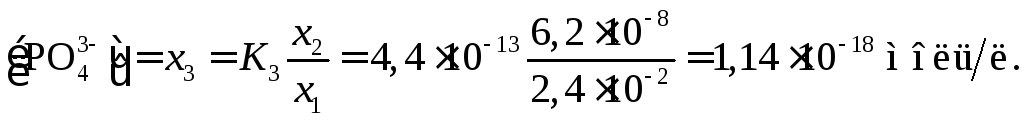
Замечание. Если не учитывать ступенчатую диссоциацию и рассчитать равновесие суммарной реакции, получим ошибочные результаты. Действительно, учитывая соотношение (x<<c_), получим

Такой расчет дает концентрацию ионов водорода на 4 порядка меньше, а концентрация ионовна 11 порядковбольшеистинной величины.