
ledenev-a
.pdf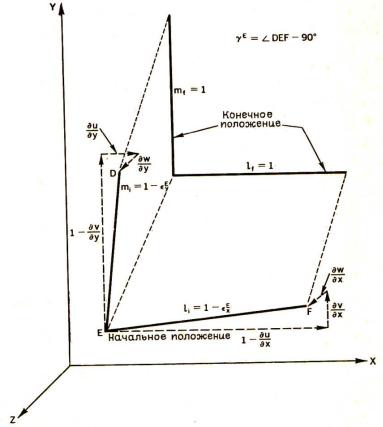
|
L |
|
∂u |
|
∂v |
|
∂u ∂u |
|
∂v ∂v |
|
∂w ∂w |
|
|
|
1 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
γ xy |
= arcsin |
|
+ |
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
; |
||||||
∂y |
∂x |
|
∂x |
|
∂y |
∂x ∂y |
|
∂x |
|
|
|
L |
L |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
(1 + εx )(1 + ε y ) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
∂v |
|
∂w |
|
|
∂u ∂u |
|
|
∂v ∂v |
|
|
∂w ∂w |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
γ yz |
= arcsin |
|
+ |
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
∂z |
∂y |
|
∂y |
|
∂z |
|
∂y ∂z |
|
∂y |
|
|
|
|
|
(1 + ε |
L |
)(1 + ε |
L |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
y |
z |
) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
L |
|
∂w |
|
∂u |
|
|
∂u ∂u |
|
|
∂v ∂v |
|
|
∂w ∂w |
|
|
|
1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
γ zx |
= arcsin |
|
+ |
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
∂x |
∂z |
|
∂x |
|
∂z |
|
∂x ∂z |
|
∂x |
|
|
|
|
|
(1 + ε |
L |
)(1 + ε |
L |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
z |
x |
) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при Эйлеровом представлении (рис. 2.5):
Рис. 2.5. Начальное и конечное положения двух линейных элементов (первоначально параллельных декартовым осям) в поле однородной деформации при Эйлеровом представлении деформации
51
|
E |
|
∂u |
|
|
∂v |
|
|
∂u ∂u |
|
|
∂v ∂v |
|
|
∂w ∂w |
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
γ xy |
= arcsin |
|
+ |
|
|
|
|
− |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||||||
∂y |
∂x |
|
∂x |
|
∂y |
∂x ∂y |
|
∂x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
(1 − εLx )(1 − εLy ) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
∂v |
|
|
∂w |
|
|
|
∂u ∂u |
|
|
|
∂v ∂v |
|
|
|
∂w ∂w |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
γ yz |
= arcsin |
|
+ |
|
|
|
|
− |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
||
∂z |
|
∂y |
|
∂y |
|
∂z |
|
∂y ∂z |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
(1 − εLy )(1 − εLz ) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
∂w |
|
|
∂u |
|
|
|
∂u ∂u |
|
|
|
∂v ∂v |
|
|
|
∂w ∂w |
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
γ zx |
= arcsin |
|
|
+ |
|
|
|
|
− |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
∂x |
|
∂z |
|
|
∂x |
|
∂z |
|
|
∂x ∂z |
|
|
∂x |
|
|
|
|
|
|
(1 − ε |
L |
)(1 |
− ε |
L |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
z |
x |
) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∙ При малых поворотах
Линейные деформации. Если производные в поперечном направлении достаточно малы, чтобы их квадратами можно было пренебречь по сравнению с первой производной в направлении рассматриваемого перемещения. При этом предположении уравнения для линейных деформаций принимают следующий вид:
L |
|
∂u |
ε x |
= |
, |
|
|
∂x |
E |
|
∂u |
εx |
= |
, |
|
|
∂x |
Деформация сдвига
|
|
∂v |
|
εL = |
|
, |
|
y |
|
|
|
|
|
∂y |
|
|
|
∂v |
|
εE |
= |
|
, |
|
|||
y |
|
|
|
|
|
∂y |
|
εLz
εEz
=∂w .∂z
=∂w .∂z
при Лагранжевом представлении:
γ |
L |
= arcsin |
|
∂u |
+ |
∂v |
+ |
∂v |
+ |
∂u |
|
|||||
xy |
|
∂y |
|
∂y |
|
|
1 |
∂x |
|
|
, |
|||||
∂x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при Эйлеровом представлении:
E |
∂u |
|
∂v |
|
∂v |
∂u |
|||
γ xy |
= arcsin |
|
− |
|
|
+ ∂x |
1 − |
∂x |
. |
|
|||||||||
∂y 1 |
∂y |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∙ При малых деформациях
Линейные деформации
при Лагранжевом представлении:
L |
|
∂u |
|
1 |
|
∂u |
2 |
|
∂v |
2 |
|
∂w |
2 |
|
|
|
|
|
|
|
|
||||||||
ε x |
= |
∂x |
+ |
|
|
|
|
+ |
|
|
+ |
|
|
, |
2 |
|
|
|
|||||||||||
|
|
|
|
∂x |
|
|
∂x |
|
|
∂x |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
52
при Эйлеровом представлении:
E |
|
∂u |
|
1 |
|
∂u |
2 |
|
|
|
|
||||
ε x |
= |
∂x |
− |
|
|
|
|
2 |
|
||||||
|
|
|
|
∂x |
|
||
|
|
|
|
|
|
|
|
|
∂v 2 |
|
∂w |
2 |
|
+ |
|
|
+ |
|
. |
|
|||||
|
∂x |
|
∂x |
|
|
|
|
|
|
|
|
Деформации сдвига
при Лагранжевом представлении:
γ Lxy |
= |
∂u + |
∂v + |
∂u ∂u + |
∂v |
|
∂v |
+ |
∂w ∂w , |
|
|
||||||||
|
|
∂y |
∂x |
∂x ∂y |
∂x ∂y |
∂x ∂y |
|||
при Эйлеровом представлении:
γ E |
= ∂u + ∂v |
− ∂u |
∂u |
− |
∂v |
|
∂v |
− |
∂w |
∂w . |
|
|
|
|
|||||||
xy |
∂y ∂x |
∂x ∂y ∂x ∂y |
|
∂x ∂y |
||||||
|
|
|||||||||
∙ При малых поворотах и малых деформациях
Линейные деформации
ε x = ∂u / ∂x.
Деформации сдвига
γ = |
∂u + |
∂v . |
xy |
∂y |
∂x |
|
|
2.3. УРАВНЕНИЯ СОВМЕСТНОСТИ ДЕФОРМАЦИЙ СЕН-ВЕНАНА
|
∂2γ xy |
= |
|
∂2ε |
|
+ |
|
∂2ε y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∂x∂y |
|
|
|
∂y2 |
|
∂x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∂2γ yz |
= |
|
∂2ε y |
|
+ |
∂2ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∂y∂z |
|
|
|
∂z2 |
|
∂y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
∂2γ |
zx |
= |
|
∂2ε |
z |
+ |
|
∂2ε |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∂z∂x |
|
|
|
∂x2 |
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
∂γ |
|
|
|
|
|
|
∂γ xy |
|
|
|||||||||||||||||
|
|
∂ |
2ε |
x |
|
|
|
|
∂ |
|
|
|
∂γ yz |
|
|
|
|
|
zx |
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
= |
|
|
|
− |
|
|
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
|
|
|
|
; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∂y∂z |
|
|
|
|
∂x |
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
∂z |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
∂ |
2ε y |
|
|
|
|
∂ |
|
|
∂γ yz |
|
|
|
|
|
∂γ |
zx |
|
|
|
|
∂γ xy |
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
|
; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∂z∂x |
|
|
|
|
∂y |
|
|
∂x |
|
|
|
|
|
|
∂y |
|
|
|
|
|
∂z |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
∂ |
2 |
εz |
|
|
|
∂ |
|
|
∂γ |
yz |
|
|
|
|
|
|
|
∂γ zx |
|
|
|
|
∂γ |
xy |
|
|
|
|
|
|||||||||
2 |
|
= |
|
|
|
|
|
+ |
|
− |
|
|
|
|
. |
|
|
|||||||||||||||||||||||
|
|
|
|
∂z |
|
|
|
|
|
|
|
∂z |
|
|
||||||||||||||||||||||||||
|
|
∂x∂y |
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
53
2.4. ДВИЖЕНИЕ СПЛОШНОЙ СРЕДЫ
Рассмотрим теорию Л.И. Седова [30]. Движения определяются по отношению к некоторой прямолинейной или криволинейной системе координат. Линии, на которых какие-либо координаты сохраняют постоянные значения, называют координатными. Касательные к координатным линиям образуют триэдр. Если координатные линии
x1, x2 , x3 прямые, то система координат прямолинейная, если кривые – криволинейная.
Движение точки относительно системы координат x1, x2 , x3
xi = f i (t) , i = (1, 2, 3) .
Функции xi называются законом движения точки.
Сплошная среда – непрерывная совокупность точек. Координаты точек в начальный момент времени t0 обозначают a, b, c или
ξ1, ξ2 , ξ3 , а в любой момент времени – |
x1, x2 , x3 . |
||
Законом движения континуума является |
|||
х1 = х1 (a, b, c, t); |
|
|
|
x2 = x2 (a, b, c, t); |
или |
xi = хi (a, b, c, t) . |
|
x3 = x3 (a, b, c, t). |
|
|
|
|
|
|
|
|
|
|
|
Если a, b, c фиксированы, а t – переменная, то будет закон движения одной точки; а если a, b, c – переменные, а t – фиксирована, то функции дадут распределения точек континуума в пространстве в данный момент времени; если a, b, c и t – переменные, то формулы опреде-
ляют движение сплошной среды. Основная задача механики сплош-
ной среды заключается в определении ранее записанных функций.
Лагранжевы переменные. Координаты a, b, c или ξ1, ξ2 , ξ3 ,
индивидуализирующие точки контура и время t, называют переменными Лагранжа. В кинематике сплошную среду рассматривают как абстрактный образ, а не только как материальное тело. При изучении деформаций опираются на аппарат дифференциального и интегрального исчисления. Функции, входящие в закон движения континуума, имеют непрерывные частные производные по всем аргументам.
Решение ранее приведенного уравнения можно представить в виде
ξi = ξi (x1, x2 , x3 , t) .
54
Закон движения можно рассматривать как взаимно-однозначное и непрерывное отображение области деформируемого тела в различные моменты времени.
В Лагранжеву систему координат входят и сопутствующие ко-
ординаты ξ1, ξ2 , ξ3 индивидуальных точек, т.е. подвижная деформи-
руемая криволинейная система координат. Все точки сплошной среды покоятся относительно подвижной сопутствующей системы координат
ξ1, ξ2 , ξ3 . Эти координаты не меняются, а сама система движется,
растягивается, сжимается, извивается. Таким образом, когда необходимо индивидуализировать точки, то пользуются Лагранжевыми координатами. При этом подразумевается наличие системы отсчета
x1, x2 , x3 .
Скорость индивидуальной точки относительно системы отсче-
та x1, x2 , x3 – v = ∂z / ∂t , где z – радиус-вектор, зависящий в общем
случае от ξ1, ξ2 , ξ3 . Относительно сопутствующей системы координат
среда покоится.
Ускорение точки сплошной среды
|
∂v |
ξ |
|
, |
a = |
|
|
||
|
∂t |
|
i |
|
где ai = ai (ξ1, ξ2 , ξ3 , t) – компоненты ускорения.
Таким образом, с точки зрения Лагранжа нас интересует история движения индивидуальных точек сплошной среды.
Переменные Эйлера. С точки зрения Эйлера рассматривают, что происходит в разные моменты времени в данной геометрической точке
пространства. Геометрические координаты пространства x1, x2 , x3 и
время t носят название переменных Эйлера. Движение считается
известным, если
v = v (x1, x2 , x3 , t) ; a = a (x1, x2 , x3 , t) ; T = T (x1, x2 , x3 , t) .
При фиксированных x1, x2 , x3 и переменном t определяют изме-
нения во времени скорости, ускорения, температуры и т.д. в данной точке пространства для различных приходящих в эту точку частиц.
При фиксированном t и переменных x1, x2 , x3 функции дают
распределения характеристик движения в пространстве в данный момент времени.
55
При переменных x1, x2 , x3 и t определяют распределения харак-
теристик движения в пространстве в разные моменты времени. Рассмотрим переход от переменных Лагранжа к переменным Эй-
лера. По Лагранжу закон движения сплошной среды
xi = xi (ξ1, ξ2 , ξ3 , t) .
Решив его относительно ξ1, ξ2 , ξ3 , получают
ξi = ξi (x1, x2 , x3 , t) ,
т.е. переходят к переменным Эйлера.
При фиксированных x1, x2 , x3 указывают те точки ( ξ1, ξ2 , ξ3 ),
которые в разные моменты времени приходят в данную точку пространства.
При изучении движения рассматривают скалярные и векторные величины. Совокупность значений той или иной величины, заданных в каждой точке рассматриваемой области, называются полем этой величины. Поля могут быть скалярными и векторными.
Процессы и движения считаются установившимися, если характеризующие их величины не зависят явно от времени. Для каждого поля, например, скорости, можно построить линии тока, по которым с точностью до направления известен вектор.
Упругое тело – среда, в которой компоненты тензора в каждой частице являются функциями компонента тензора деформации, компонент метрического тензора, температуры и других параметров физикохимической природы. Раздел механики сплошной среды, в котором изучается поведение сплошных сред, подчиняющихся закону Гука,
носит название теории упругости.
2.5. ТЕОРИИ ДЕФОРМАЦИЙ
Рассматривается система координат x1, x2 , x3 , относительно которой движется тело, положение его в начальный момент времени t0 и
в некоторый произвольный момент t. С каждой точкой движущегося тела связывают сопутствующую (с телом) систему координат
о
ξ1, ξ2 , ξ3 . Векторы базиса в момент времени t0 Эi и в момент t0 ξˆ i будут разными. Для абсолютно твердого тела, в которого вморожена
о
система ξ1, ξ2 , ξ3 , триэдры Эˆ i можно получить из триэдров Эi путем поступательного перемещения и поворота.
56
В случае деформируемого тела расстояние между точками меняется, т.е. тело сжимается, растягивается, искривляется. Координатные линии, сопутствующие системе координат, деформируются. Изменя-
ются во времени и углы между векторами базиса Эˆ i .
Коэффициент относительно удлинения l
l = (ds − ds′) / ds′ ,
где ds и ds′ проходят в соответствующие моменты времени через одни и те же индивидуальные точки.
Если коэффициент l в каждой точке деформируемой среды и в каждом направлении мал, то деформация называется малой, если l имеет конечные значения, то деформация конечная.
Деформации в момент времени t зависят не только от рассматриваемого состояния, но и от какого-то начального. За начальное состояние может быть принято состояние, в котором структура каждого элемента сплошной среды упорядочена и на него не действуют никакие силы.
Уравнения движения
|
∂σ |
xx + |
∂σ xy |
+ |
|
∂σ |
|
|
|
+ ρX = ρ |
∂ |
2u |
|
|||||||||
|
|
|
|
|
xz |
|
|
|
|
1 |
; |
|||||||||||
|
|
∂σ y |
|
∂σz |
|
∂t 2 |
||||||||||||||||
|
∂σ x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∂σ yx |
+ |
∂σ yy |
|
+ |
|
∂σ yz |
+ ρY = ρ |
∂ |
2u |
2 |
; |
||||||||||
|
∂σx |
∂σ y |
|
|
∂σz |
|
∂t 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∂σ |
zx |
+ |
∂σ zy |
+ |
∂σ |
zz |
+ ρZ = ρ |
∂ 2u |
3 |
, |
|||||||||||
|
∂σ x |
∂σ y |
|
∂σ z |
∂t 2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где σij – компоненты тензора напряжений; |
X, |
Y, |
Z – проекции объем- |
|||||||||||||||||||
ной силы F на оси x, y, z; ρ – плотность среды; |
|
ui |
|
– |
компоненты векто- |
|||||||||||||||||
ра смещения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эту систему можно записать в виде |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
&& |
|
|
|
|
|
|
|
|
|
|
|
|
σij, j + ρ(Fi − ρu1 ) = 0. |
|
|
|
|
|
|
|||||||||||||
Зависимость между тензором деформации и вектором перемеще- |
||||||||||||||||||||||
ний (уравнение Коши) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∂u |
|
|
|
|
1 |
|
|
∂u |
∂u |
|
|
|
|
|
||||
|
ε = |
1 ; |
|
ε = |
|
|
|
|
|
1 |
+ |
|
|
2 |
; |
|
||||||
|
|
2 |
|
∂x |
|
|
|
|
||||||||||||||
11 |
|
∂x |
12 |
|
|
2 |
|
∂x |
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
57
ε |
|
|
= |
∂u |
|
|
ε |
|
= |
1 |
|
∂u |
|
+ |
∂u |
|
|
|
|
|
∂x |
2 ; |
|
|
|
∂x |
2 |
∂x |
3 |
|
; |
||||||
|
|
|
2 |
|
|
|||||||||||||
|
22 |
|
2 |
|
23 |
|
|
3 |
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ε |
|
= |
∂u |
|
ε |
|
= |
1 |
|
∂u |
|
+ |
∂u |
|
|
|
||
|
|
|
3 ; |
|
|
|
|
3 |
|
1 |
. |
|||||||
|
∂x |
|
2 |
∂x |
∂x |
|
||||||||||||
|
|
33 |
|
|
|
31 |
|
|
|
|
|
|
||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
3 |
|
|
||
В сокращенном виде систему записывают в виде
ε |
|
= |
1 |
|
∂u |
|
+ |
∂u |
|
|
|
|
∂x |
i |
∂x |
i . |
|||
|
2 |
|
|||||||
|
ij |
|
|
|
|
|
|||
|
|
|
|
|
i |
|
i |
||
Уравнения неразрывности или совместности деформаций СенВенана имеют вид:
|
|
|
|
|
∂2ε |
|
|
|
+ |
∂2ε |
22 |
= |
|
|
|
|
|
∂2ε |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
11 |
|
|
|
2 |
|
|
|
|
|
|
12 |
; |
|
|
|
|
|||||||||||||
|
|
|
|
|
∂x |
2 |
|
|
∂x |
2 |
∂x |
∂x |
2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∂ 2ε |
22 |
+ |
∂2ε |
33 |
= |
2 |
|
|
∂2ε |
23 |
|
; |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
∂x |
2 |
|
|
∂x |
2 |
|
∂x |
2 |
∂x |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||
|
|
|
|
|
∂2ε |
33 |
+ |
∂2ε |
= |
|
|
|
|
∂2ε |
31 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
11 |
2 |
|
|
|
|
|
|
|
; |
|
|
|
|
||||||||||||
|
|
|
|
|
∂x |
2 |
|
|
∂x |
2 |
|
∂x |
|
∂x |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|||
|
∂ |
|
|
|
∂ε |
23 |
|
+ |
∂ε |
31 |
|
− |
∂ε |
|
|
|
|
|
|
|
= |
|
∂2ε |
3 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
; |
||||||||||||||||
|
∂x |
|
∂x |
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
∂x ∂x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
∂x |
2 |
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|||||||||||||||
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||
|
∂ |
|
∂ε |
|
|
|
|
|
+ |
∂ε |
|
|
|
− |
∂ε |
|
|
|
|
|
|
|
= |
|
∂ 2ε |
|
|
; |
|||||||||
∂x |
|
|
∂x |
|
|
|
|
∂x |
|
|
|
∂x |
|
|
|
|
|
|
|
∂x ∂x |
|
||||||||||||||||
|
|
|
|
|
31 |
|
|
|
12 |
|
|
|
|
23 |
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||
|
1 |
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|||||||||
|
∂ |
|
|
|
∂ε |
|
|
|
|
+ |
∂ε |
23 |
− |
∂ε |
31 |
|
|
= |
∂2ε |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||
|
∂x |
|
|
∂x |
|
|
|
|
|
|
∂x |
|
|
|
|
|
∂x |
|
|
||||||||||||||||||
|
2 |
|
|
3 |
|
|
|
∂x |
|
|
|
2 |
|
|
|
|
|
|
∂x |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
1 |
|
|||||||
В сокращенном виде
Likl L jmnεim, kn = 0.
Однородная деформация. Потенциал перемещения. При одно-
родной деформации компоненты ui вектора перемещения u являются линейными функциями координат (С.П. Демидов, 1979)
58
ui = ui0 + cij x j ,
где ui0 и cij – постоянные.
Компоненты тензора деформаций и тензора малого поворота – постоянные величины
εij = (cij + c ji ) / 2;
ωij = (cij − c ji ) / 2,
т.е. все частицы тела деформируются одинаково.
При однородной деформации прямые линии остаются прямыми после деформации, параллельные плоскости и параллельные прямые преобразуются в параллельные плоскости и параллельные прямые после деформации, и сфера преобразуется в эллипсоид. Поле перемещений – градиент скалярного поля ψ(xi) (потенциальное поле).
Глава 3. НЕЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ
Основные сведения приведены в [38, 39].
Современная техника предъявляет повышенные требования к прочностным свойствам реализуемых машин, конструкций и сооружений, уменьшению их веса и размеров. Это приводит к необходимости создания новых методов расчета, наиболее полно и адекватно учитывающих свойства реальных материалов. За последние годы это обстоятельство заметно усилило внимание исследователей к задачам теории упругости неоднородных тел.
Линейная теория упругости неоднородных тел основана на использовании закона Гука, в котором параметры, определяющие упругие свойства среды (например, параметры Ламе) – функции координат [39]. Наиболее естественной как с математической, так и с физической точки зрения является классификация, основанная на характере зависимости параметров Ламе от координат. Целесообразно выделить три основные группы задач, в которых параметры Ламе:
а) непрерывные детерминированные функции координат; б) кусочно-постоянные функции координат; в) случайные функции координат.
Выделяют следующие три основных раздела теории упругости неоднородных тел:
а) упругие тела с непрерывной неоднородностью; б) кусочно-постоянные упругие тела; в) случайно-неоднородные упругие тела.
59
Каждый из разделов имеет свою область приложений и характеризуется определенной спецификой применяемых математических методов исследования. Разделы связаны между собой, и при решении задач какого-либо одного раздела теории упругости неоднородных тел могут быть использованы решения, полученные в других разделах.
3.1.ПОСТАНОВКА ЗАДАЧ И ОБЩИЕ ТЕОРЕМЫ
∙Основные уравнения теории неоднородных тел
В ортогональной декартовой системе координат xs (x1, x2 , x3 )
трехмерного эвклидова пространства Е3 при малых деформациях любой среды имеют место следующие основные уравнения механики сплошной среды:
–уравнения движения
|
∂σij |
|
+ ρF = ρ |
∂2u |
i |
, |
||||||
|
∂σi |
|
|
|
||||||||
|
|
|
|
i |
|
|
∂t 2 |
|
|
|||
|
|
|
|
|
|
|
|
|
||||
– формулы Коши |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
∂u |
i |
|
∂u j |
|
|
|
ε |
|
= |
|
|
|
|
+ |
|
|
, |
||
|
2 |
∂x |
|
∂x |
||||||||
|
|
ij |
|
|
j |
|
|
|
||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
–условия совместности деформаций
|
|
|
|
∂2ε |
lm |
|
1 |
|
∂u |
i |
|
∂u j |
|
||
ε |
|
ε |
|
|
|
= |
|
|
|
+ |
|
. |
|||
|
pmn ∂x |
∂x |
|
2 |
∂x |
|
∂x |
||||||||
|
ijl |
|
n |
|
|
j |
|
|
|||||||
|
|
|
|
j |
|
|
|
|
|
|
|
i |
|
||
В приведенных соотношениях |
σij |
– |
|
тензор (симметричный) на- |
|||||||||||
пряжений; εij – тензор деформаций; ui – вектор перемещений; Fi – вектор плотности массовых сил; ρ – плотность; t – время; εijl – сим-
волы Леви– Чивита.
Обобщенный закон Гука – соотношения между напряжениями σij и деформациями εij при изотермических процессах деформирования неоднородных анизотропных упругих тел
σij = cijkl (xs )σkl ,
или обратными соотношениями
εij = sijkl (xs )σkl ,
60
