Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Волгоградский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ledenev-a

.pdf

Скачиваний:

Добавлен:

15.03.2016

Размер:

8.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 325 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Силовое поле – физическое пространство, обладающее таким свойством, что на каждую материальную точку М, помещенную в это пространство, действует сила, зависящая от времени. Если сила силового поля не зависит от времени, то поле – стационарное.

Стационарное силовое поле потенциально, если проекции силы силового поля материальной точкой М на координатные оси:

F = ∂u		; F		= ∂u	; F =	∂u	,
			y
x	∂х			∂y	z	∂z

где u = u(x, y, z) – силовая функция, однозначно зависящая от координат. Сила силового поля

= i F + jF +

zF = i ∂u(x, y, z) + j ∂u(x, y, z) +

∂u(x, y, z)

∂x

∂j

∂z

Элементарная работа силы

δA =

δzˆ = F d

+ F d

∂u

= du(x, y,

∂u

∂y

∂z

z).

Таким образом, элементарная работа силы потенциального силового поля равна полному дифференциалу силовой функции.

Если точка М перемещается из положения М1 в положение М2, то конечная работа

M 2 M 2

A1, 2 = ∫ δΑ = ∫ du (x, y, z) = u2 − u1,

M1 M1

где u2 = u (x2 , y2 , z2 ), u1 = u (x1, y1, z1).

Для силы, не принадлежащей силовому полю, рассматривается криволинейный интеграл

M 2

A1, 2 = ∫ F cos α ds.

Работа упругой силы (реакция деформированной пружины)

Упругая сила пружины

Fu = −сx1,

где с – постоянный коэффициент пропорциональности (жесткость пружины), равный величине силы Fd при единичном отклонении те-

ла М от недеформированного состояния; x1 – величина растяжения

пружины.

Элементарная работа сил упругости


		δA = −cx dx.
Полная работа на перемещении M1M 2
M 2	M 2	M 2
A1, 2 = ∫δΑ = ∫(−cxdx) = − ∫cxdx =			1	c (x12 − x22 ),

M1	M1	2
		M1

где (x1 − x2 ) − дополнительная деформация. При рассмотрении упругого стержня

c = EA . l0

Работа силы упругости зависит только от начального и конечного положения тела М.

Поле напряжений, деформаций и перемещений [40]. Поля на-

пряжений и деформаций взаимно однозначны в случае линейноупругих деформаций.

В практике часто используют систему изолиний для анализа результатов измеренний. Приведем некоторые изолинии для плоского поля (рис. 1.18).

Изостаты – траектории главных напряжений, системы из двух семейств S1 и S2 взаимно ортогональных кривых, с которыми совпадают направления наибольших и наименьших главных напряжений.

Уравнение траекторий главных напряжений в дифференциальной форме имеет вид

dy	=	σ y − σ x	±	1
					(σ x − σ y )2 + 4τxy	.
dx
		2τxy		2τxy

Изоклины – геометрическое место точек поля напряжений, в которых направления главных напряжений параллельны и имеют один угол наклона ϕ0 , выбранный направлением – параметром изоклины А.

Уравнение изоклин:

tg2ϕ0 = 2τxy /(σ x − σ y ) = A .

Рис. 1.18. Характер развития кривых, равных максимальному касательному напряжению под жестким фундаментом

Изохромы – линии, соединяющие точки, в которых разности главных напряжений в рассматриваемой плоскости поля напряжений имеют одну и ту же величину.

Уравнение изохром:

σ1 − σ2 = 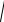(σ x − σ y )2 + 4τxy = B .

Изопахи – линии, соединяющие точки с равными значениями сумм главных напряжений.

Уравнение изопах:

σ1 + σ2 = σ x + σ y = C .

Изоэнтаты – линии, соединяющие точки с равными значениями главных напряжений (σ1 или σ2) или главных деформаций (ε1 или ε2).

Изотропы – линии одинакового жесткого поворота. Для малых деформаций:

ω = 1/ 2[(∂u / ∂y) − (∂v / ∂y)].

Изокинеты – линии одинаковой величины полного перемещения. Изопарагоги – линии одинаковых частных производных. Изотены – линии одинаковых значений главных Эйлеровых де-

формаций ε1E и ε2E .

Глава 2. ЛИНЕЙНАЯ ТЕОРИЯ УПРУГОСТИ. ТЕОРИЯ ДЕФОРМАЦИЙ

2.1. ТЕНЗОРЫ И ИНВАРИАНТЫ ДЕФОРМАЦИЙ

Обозначения приняты из книги Н.Н. Малинина (1975).

Деформированное состояние в точке тела

ε = ∂ux ; ε =

∂u y

; ε = ∂uz ;

∂x

∂y

∂z

∂u

∂u y

∂u

; γ

;

∂y

∂x

∂z

∂x

∂y

∂z

Рис. 2.1. Деформированное состояние в точке тела

Относительная объемная деформация в точке

θ = εx + ε y + εz .

Средняя объемная деформация в точке

ε		=	1	(ε		+ ε		+ ε		).
	0				x		y		z
		3

Модуль объемной деформации

K =	E
		.
	3(1− 2μ)

Тензор деформации – тензор, который характеризует сжатие (растяжение) и изменение формы в каждой точке тела при деформации

ε x

γ xy

T =

γ yz

γ zx

При тензорной записи

∂u

∂xi

Разложение тензора деформации

Tε = Tε0 + Dε ,

где

ε0

–

шаровой тензор деформаций;

ε0

e	x	e	xy	e
					xz
Dε = eyx		ey		eyz –		девиатор деформаций;
		ezy
ezx				ez

ε x = ε x − ε0 , ε y = ε y − ε0 , ε z = ε z − ε0 ;

γ xy

γ yz

, ε

В тензорной записи

e = ε

− δ

;

εij

Первый, второй и третий инварианты тензора деформаций и

зависимость между ними

I1 (Tε ) = ε x + ε y + ε z ;

(T ) = −ε

− ε

γ 2xy

γ 2yz

γ 2zx

;

ε x

γ xy

γ yz

(T ) =

γ xy

γ yz

γ zx

ε z

ε3 − j (T ) ε

2 − j

(T ) ε − j

(T ) = 0.

Инварианты тензора деформации через главные деформации

j1 (Тε ) = ε1 + ε2 + ε3 ;

j2 (Тε ) = −ε1ε2 − ε2ε3 − ε3ε1 ;

j3 (Тε ) = ε1ε2ε3 .

Компоненты девиатора деформации

j1 (Dε ) = 0 ;

(D ) = ε

− ε

+ ε

+ ε2

(ε

− ε

+ (ε

− ε

)2 + (ε

− ε

(γ 2

+ γ 2

)

;

			ε		x	ε	xy
					x		xy
j (D ) = ε						ε
3	ε			xy				y
		ε		zx		ε	yz
				zx			yz

εzx

εyz .

εx

Интенсивность деформаций – это величина, пропорциональная квадратному корню из второго инварианта девиатора деформаций

																																							→
ε		=		4				(D ) = U								=			2
																							(ε		− ε					)2 + (ε					− ε		)2	+
					j										3
			3		j										3			3
	i		3			2		ε										3						x					y					y		z
		→
		→	+ (ε					− ε		)2		+	3	(γ 2				+ γ2				+ λ2					) =				2	e e =
													3																		2
																														3
						z			x				2 xy							yz				zx						3			ij ij
			2
		=	2				(ε − ε				2	)2 + (ε					2	− ε		3	)	2 + (ε				3		− ε )2					,


			3					1																						1
			3

где U = 4 j2 (Dε ) – интенсивность угловых деформаций.

Интенсивность пластических деформаций

→

ε p =

(ε p − ε p )2

+ (ε p − ε p )2

+ (ε p

− ε p )2

→

(γ p

)2 + (γ p

e p e p .

ij ij

Октаэдрическая угловая деформация

γ	0	=	2		(ε − ε	2	)2	+ (ε	2	− ε	3	)2	+ (ε	3	− ε )2	.

		3		1											1

Закон Гука:

–при растяжении– сжатии

ε x = σ x / E, ε x = ε y = −μεz ;

–при плоском чистом сдвиге

γ= τ / G ;

–при двухосном растяжении

(σ

− μσ

);

(σ

− μσ

);

= −

(σ

+ σ

);

–для плоского напряженного состояния

(σ

− μσ

) ;

(σ

− μσ

);

= τ

/ G; ε

= −

(σ

+ σ

);

–при трехосном растяжении

[σ

− μ(σ

+ σ

)];

= τ

/ G ;

[σ

− μ(σ

+ σ

)];

= τ

/ G ;

[σ

− μ(σ

+ σ

)];

= τ

/ G .

2.2. ОБЩИЕ СООТНОШЕНИЯ МЕЖДУ ДЕФОРМАЦИЯМИ И ПЕРЕМЕЩЕНИЯМИ [22]

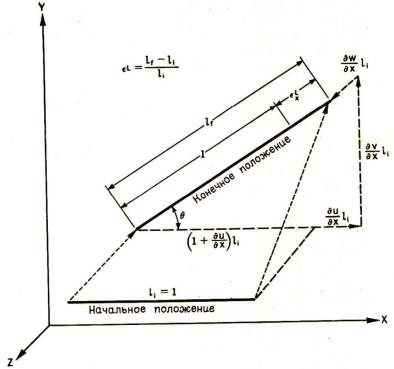
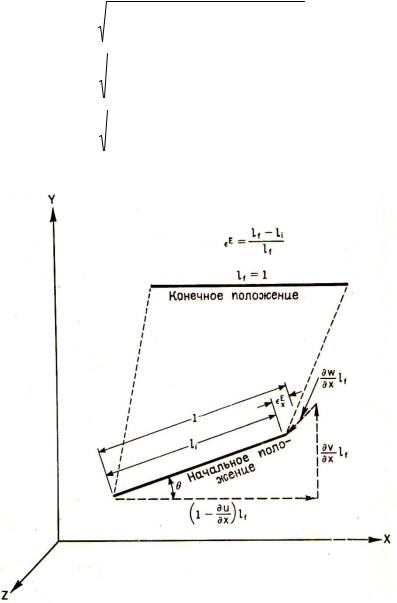
∙ При больших поворотах и больших деформациях (рис. 2.2)

Линейные деформации:

при Лагранжевом определении деформации:

Рис. 2.2. Начальное и конечное положения линейного элемента в поле однородной деформации при Лагранжевом определении деформации

εLx =

εLy =

εLz =

∂u

∂u 2

∂v 2

∂w

1 + 2

−1;

∂x

∂v

∂u 2

∂v 2

∂w

1 + 2

−1;

∂y

∂w

∂u 2

∂v 2

∂w

1+ 2

−1,

∂z

при Эйлеровом определении деформации (рис. 2.3):

Риc. 2.3. Начальное и конечное положения линейного элемента в поле однородной деформации при Эйлеровом определении деформации

εEx = 1−

εEy = 1−

εEz = 1−

∂u

∂u 2

∂v 2

∂w

1− 2

;

∂x

∂v

∂u 2

∂v 2

∂w 2

1− 2

;

∂y

∂w

∂u 2

∂v 2

∂w

1− 2

∂z

Деформация сдвига:

при Лагранжевом представлении (рис. 2.4):

Рис. 2.4. Начальное и конечное положения двух линейных элементов (первоначально параллельных декартовым осям) в поле однородной деформации при Лагранжевом определении деформации

<<< < Предыдущая 1 2 3 45 / 325 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.04.20151.4 Mб91konstruktsii.doc
#
10.04.2015936.96 Кб31Korobki-Volgograd.doc
#
04.05.2015225.79 Кб19kursovaya_глинозем.doc
#
03.12.2018448.83 Кб14KURSOVOJ_PROYeKT_FROLOV_M_S_401-T.docx
#
13.08.201983.97 Кб9Laboratornaja_rabota_No3_Struktury.doc
#
15.03.20168.17 Mб55ledenev-a.pdf
#
19.12.20182.17 Mб7Lektsia_10_EMM__1.doc
#
29.07.2019111.1 Кб8Lektsia_12_BD.doc
#
19.12.201877.82 Кб8Lektsia_5_Excel.doc
#
29.07.201973.22 Кб6Lektsia_6_Modelir.doc
#
29.07.201990.62 Кб4Lektsia_8_stilm_Yap.doc