ledenev-a

Ex = E1z ν ,

где ν – показатель степени неоднородности. Тогда

σz = νPz ν /(2πRν+2 ).

Вкниге Г.И. Марчука и В.И. Агошкова (1981) описаны проекци- онно-сеточные методы (Ритца, Бубнова– Галеркина, наименьших квадратов и др.), кусочно-линейные аппроксимации, методы решения некоторых краевых задач, рассмотрены примеры построения базисных функций.

Методы вычислительной математики изложены и в ранее изданной книге Г.И. Марчука (1977). Большое внимание уделено итерационным методам.

Глава 5. НЕЛИНЕЙНЫЕ ЗАДАЧИ

Подробнее см. в [6, 10, 12, 15, 20, 21, 25, 29, 47, 58, 68, 70, 75, 82, 83].

5.1. ПРИМЕНЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНОЙ МЕХАНИКИ ГРУНТОВ

Это механика, разрешающая система уравнений которой нелинейна. В качестве объекта исследования является среда с двумя основными особенностями: с внутренним трением и многокомпонентностью (обычно трехкомпонентная среда – частицы грунта + вода + воздух).

Нелинейность разрешающей системы проявляется в трех случаях:

1)при зависимости консолидационных параметров от изменяющейся пористости – нелинейные консолидационные свойства;

2)при нелинейной связи между напряжениями, деформациями и их производными во времени – физическая нелинейность;

3)при нелинейной связи между компонентами деформаций и градиентами перемещений – геометрическая нелинейность.

Для решения задач используются уравнения состояния, вытекающие из теории пластичности. В основе теории пластического течения лежит принцип максимума Мизеса: скорость диссипации механической энергии в единице объема во время пластического деформирования имеет максимальное значение для действительного напряженного состояния из всех возможных, допускаемых данным критерием пластичности.

91

Принимают следующие допущения:

– поверхность нагружения не должна быть вогнута; направление вектора приращения пластических деформаций должно совпадать с нормалью к поверхности нагружения в точке нагружения (ассоциированный закон пластического течения).

При учете вязкопластичности вводят понятие мгновенной поверхности нагружения.

К числу основных факторов, определяющих процесс деформирования, относят:

−физическое состояние грунта;

−деформацию грунтов при активном нагружении;

−пластические деформации, зависящие нелинейно от напряжения, а также от пути нагружения и вида напряженного состояния;

−дилатацию (доуплотнение или разуплотнение), зависящую от плотности грунта, его физического состояния, степени приближения к предельному состоянию, траектории нагружения, характера воздействия;

−многофазность грунтов;

−запаздывание пластических деформаций во времени, особенно для связных грунтов;

−характер воздействия (статические, температурные, коррозионные, динамические нагружения).

Для анализа нелинейного поведения грунтов используют различные методы вычислительной математики: конечно-разностные, вариа- ционно-разностные, конечных и граничных элементов и др.

Кроме того, используют и другие нелинейные методы расчета:

−нелинейную деформационную теорию пластичности;

−ассоциированный закон пластического течения Друккера– Прагера, неассоциированный закон пластического течения, критического состояния, пластического течения с упрочнением, обобщенный ассоциированный закон течения упрочняющихся пластических сред и др.

Величины пластических деформаций зависят от пути нагружения

ивида напряженного состояния. При сдвиге грунт либо доуплотняется (контракция), либо разуплотняется. Знак и величина дилатационной части объемной деформации зависят от: плотности грунта, степени приближения к предельному состоянию, траектории нагружения. Пластические деформации запаздывают во времени. Время запаздывания зависит от вида грунта, величины и характера воздействия.

Феноменологическое описание реологических процессов в грунтах проводится на основе теории наследственной ползучести, теорий течения и упрочнения.

92

5.2. ОСНОВЫ ТЕОРИИ ПЛАСТИЧНОСТИ

Изложенная в [23, 25, 29, 46, 68, 75, 82, 83] теория деформирования систем из упруго-идеальнопластического материала, для которого соблюдается ассоциированный закон пластического течения, в которой сохраняется гипотеза о малости суммарных упругопластических деформаций. Теория идеальной пластичности игнорирует многие усложнения, например, упрочнение и эффект Баушингера. Построение теории пластичности (Треска, Сен-Венана, Мизеса) следовало принципу пластического течения, т.е. установлению связи между скоростями тензора деформаций и тензора напряжений. Пластичность называется идеальной, если в процессе нагружения не происходит изменения поверхности пластичности. Развитию теории пластичности способствовали работы Рейса, Прагера и Койтера.

Теория течения упрочняющихся тел развивалась трудами Мелана, Прагера, Койтера, Хилла. Деформационная теория пластичности формировалась параллельно (А.А. Илюшин, Г. Генки, В.Д. Клюшников). Наибольшего успеха теория идеальной пластичности получила при разработке теории предельного равновесия (А.А. Гвоздев, 1936). Сформированы три основные теоремы:

−первая теорема (статическая) – предельная нагрузка не ниже той, которая соответствует статически допустимому полю напряжений;

−вторая (кинематическая) теорема – предельная нагрузка не выше той, которая соответствует кинематически возможному механизму пластического деформирования;

−третья теорема (двойственная) – максимум нагрузки по первой теореме и минимум по второй совпадают и равны предельной нагрузке для конструкции.

Выявлены механизмы пластического разрушения (Г. Генки, 1948), позволяющие конструировать поля скоростей деформаций по характеристикам уравнений течения. Рассмотрено образование разрывов в полях перемещений (Р. Хилл, 1956; Д.Д. Ивлев, 1966).

Исследованию механизма разрушения пластин и оболочек посвящены работы А.Р. Ржаницына, В.З. Власова, С.П. Тимошенко.

Физической основой теории пластичности является способность материалов деформироваться без заметного увеличения нагрузок (пластическое течение). При этом напряжение в материале достигает определенного значения (предела текучести).

Деформации разделяют на упругие и пластические:

εij = εijel + εij pl .

93

Поверхность нагружения (предельная поверхность в теории пластичности) также разделяет составляющие полных деформаций. В теории идеальной пластичности поверхность нагружения считается фиксированной и не зависит от истории деформирования.

Уравнение предельной поверхности (условие пластичности) имеет вид

F(s) = 0.

Если F(s) < 0 , то деформации, вызываемые малыми изменения-

вующее напряжению s .

Из постулата следует, что поверхность пластичности ограничивает выпуклую область > и вектор приращения пластической деформа-

ции перпендикулярен к поверхности пластичности в точке s . Уравнение, связывающее скорости пластических деформаций с

напряженным состоянием, называют ассоциированным законом пластического течения

где λ – параметр, пропорционально которому изменяется внешняя нагрузка.

Условия пластичности (Треска, Сен-Венана), по которым течение происходит при достижении максимальными касательными напряжениями определенного уровня (σт), следующие:

94

max ( σi , σi − σ j )− σт ≤ 0 ,

i, j =1,2,3

где si , i = 1, 2, 3 – главные напряжения; sт – предел текучести при одноосном напряженном состоянии; главные касательные напряжения tк = 12(si - s j ), k ¹ i, i ¹ j, k ¹ j .

По Мизесу условие пластичности имеет вид

(s1 - s2 )2 + (s2 - s3 )2 + (s1 - s3 )2 - s2т £ 0.

Условия Треска– Сен-Венана описывают нерегулярную поверхность пластичности с ребрами, а Мизеса – регулярную – эллипсоид вращения.

Для краевой задачи имеем:

уравнение равновесия, заданное на объеме:

sij, j + xi = 0 ,

краевые условия в напряжениях

sij n j = pi ,

условия Коши

eij = 1 (ui, j + u j,i ),

2

где n – вектор нормали к поверхности, ограничивающей тело; x , p – векторы скоростей изменения внешней нагрузки; eij , ui, j , u j,i – скоро-

сти напряжений, деформаций и перемещений.

Предполагается скачкоообразный переход из упругого в пластическое состояние (диаграмма Прандтля или жесткопластического тела).

Состояние пластического механизма системы характеризуется условиями (состояние предельного равновесия по А.А. Гвоздеву):

-система находится в равновесии;

-усилия не превосходят предельных величин и удовлетворяют условиям пластичности;

-система может деформироваться без изменения внутренних и внешних сил;

-момент в пластических шарнирах равен пластическому. Деформируемая система рассматривается как некоторая кинема-

тическая цепь с заданным числом степеней свободы. Начальная конфигурация системы – недеформированное состояние. Множества де-

95

формированных состояний порождает пространство этих состояний (метрическое пространство).

В аналитической механике деформации рассматривают как перемещения вдоль связей системы.

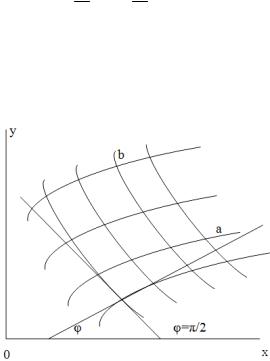
Линии скольжения – два ортогональных семейства линий, касательные в каждой точке которых совпадают по направлению с площадками скольжения (рис. 5.1). Последние в каждой точке ортогональны. На площадках скольжения касательные напряжения обладают экстремальными свойствами: они максимальны по сравнению с касательными напряжениями на соседних площадках, проходящих через ту же точку. Касательные к линиям скольжения образуют угол θ + (π / 4) и θ + (3π / 4) с осью Ox1 . Примером линий скольжения яв-

ляются линии Чернова.

Дифференциальные уравнения семейств линий скольжения имеют вид [40]

dy = tgϕ, dy = −ctgϕ. dx dx

Напряженное состояние в условиях плоской деформации можно рассматривать как наложение всестороннего равного растяжения с главными напряжениями σ0 на чистый сдвиг с касательным напряже-

нием τmax ; бесконечно малый элемент, выделенный линиями сколь-

Рис. 5.1. Линии скольжения

96

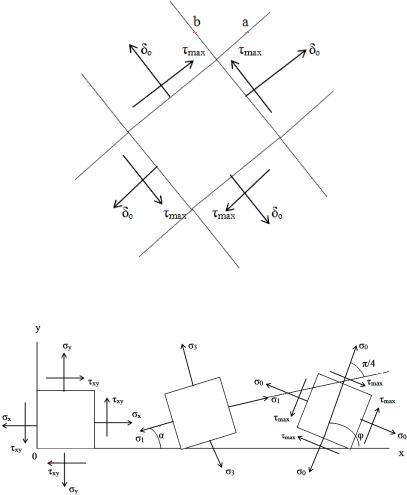
жения, испытывает одинаковое растяжение в направлении линий скольжения (рис. 5.2).

Свойства линий скольжения сформулированы в теоремах Г. Генки. Выделены центрированное и равномерное поле линий скольжения. Изменение полной скорости вдоль линий скольжения равно нулю (рис. 5.3).

В [36] рассмотрели линии разрыва в скоростях перемещений.

Рис. 5.2. Напряженное состояние элемента, выделенного линиями скольжения

Рис. 5.3. Напряжения в различных площадках в условиях плоской деформации

97

5.3. УРАВНЕНИЯ ПЛАСТИЧЕСКОГО СОСТОЯНИЯ

Формула условий текучести для изотропных тел имеет вид

f (σij ) = f ( j1, j2 , j3 ) = K 2 .

Для идеального пластического материала K 2 = const . Полагая,

что среднее нормальное напряжение не влияет на условия текучести, последнее можно представить с помощью компонента дивиатора напряжений

точки.

По Губерту М. и Мизесу Р. условием текучести является постоянство интенсивности касательного напряжения

где σ12 – касательная напряжения в случае чистого сдвига.

На основе результатов экспериментов Треска предложено применять во всех случаях максимальное касательное напряжение равным σS / 2 , т.е. наибольшему касательному напряжению в случае простого

растяжения. Математическая формулировка этого предложения дана Сен-Венаном в виде

2| σ12 | = | σ23 − σ13 | ≤ σ3 ; 2| σ23 | = | σ31 − σ12 | ≤ σ3 ; 2| σ31 | = | σ12 − σ23 | ≤ σ3.

Пластическая деформация влечет за собой некоторое упрочнение, и предел упругости повышается в направлении деформирования.

При сложном напряженном состоянии вводят в рассмотрение поверхность нагружения. Она определяет области упругого и пластического деформирования. Форма и положение поверхности нагружения зависит от текущего напряженного состояния и от всей предыдущей истории нагружения.

98

Условие изотропного упрочнения выражается через квадратичный инвариант девиатора напряжений

T = f (q),

где Т – интенсивность касательного напряжения.

При f (q) = σ12 получают условие Губерта– Мизеса. Если Т =

= g(Г)F, где g(Г) – функция, характеризующая данный материал (модуль пластичности); Г – интенсивность деформаций сдвига, то за меру упрочнения принимают работу пластической деформации

AP = ∫σij deij( P) ,

где eij( P) – компоненты пластической деформации.

5.4. КРИТЕРИИ НАЧАЛА ПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ

Полагают, что до некоторого уровня напряженного состояния имеют место лишь упругие деформации. На этом этапе напряженное состояние не зависит от пути нагружения. Граница между упругим состоянием и следующим состоянием пластического деформирования в окрестности исследуемой точки есть функция напряженного состояния

f (σ1, σ2 , σ3 ) = 0 ,

где f – поверхность текучести. Для изотропного тела

f [(I1 (Tσ ), (I 2 (Tσ ), (I3 (Tσ )] = 0.

Полагая, что σ2 не влияет на свойства пластичности материала,

f [(I 2 (Tσ ), (I3 (Tσ )] = 0.

Это уравнение цилиндрической поверхности, перпендикулярной плоскости

σ1, σ2 , σ3 = 3σ0 .

Плоскость, равнонаклонная к осям 01, 02, 03, называется девиаторной. Конец вектора

s = s1e1 + s2e2 + s3e3 ,

где s1 = σ1 − σ0 , s2 = σ2 − σ0 , s3 = σ3 − σ0 – главные составляющие девиатора тензора напряжений лежат в девиаторной плоскости.

99

Состояние пластического деформирования достигается, если изображающая точка (конец вектора σ = σ1e1 + σ2e2 + σ3e3 ) выходит на

цилиндрическую поверхность (поверхность текучести), заключенную между описанной и вписанной призмами.

Уравнение окружности цилиндра (след в девиаторной плоскости)

(σ1 − σ2 )2 + (σ2 − σ3 )2 + (σ3 − σ1 )2 = 2σT2 .

Так как изображающая точка может находится либо на грани шестигранной призмы, либо на ребре, то условие пластичности можно записать в виде

max(σ1 − σ2 , σ2 − σ3 , σ3 − σ1 )= σT ,

max(σ1 − σ0 , σ2 − σ0 , σ3 − σ0 )= 2 3 σT .

Учитывая, что главные касательные напряжения выражаются через главные нормальные напряжения

τ12 = (σ1 − σ2 )/ 2, τ23 = (σ2 − σ3 )/ 2, τ31 = (σ3 − σ1 )/ 2,

то выше записанные критерии пластичности называют соответственно критерием наибольшего касательного напряжения и критерием интенсивности касательных напряжений

τ122 + τ223 + τ312 = (1/ 2)σT2 .

Для плоского напряженного состояния (например, σ3 = 0 ) условие наибольшего касательного напряжения

max (σ1 − σ2 , σ2 , σ1 )= σT .

Этому условию соответствует шестигранник. Условие наибольшего приведенного напряжения

max (σ1 − σ2 / 2 , σ2 − σ1 / 2 , (σ1 − σ2 ) / 2 )= σT .

100