
ledenev-a
.pdfИнварианты для ортотропного тела
I |
1 |
= a′ |
+ a′ |
+ 2a′ |
|
= |
1 |
+ |
1 |
− |
2μ12 |
, |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
11 |
22 |
|
|
|
12 |
|
|
|
E1 |
|
|
E2 |
|
|
|
E1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
I |
2 |
= a′ |
− 4a′ |
|
= |
|
1 |
|
+ |
4μ12 |
, |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
00 |
12 |
|
|
G |
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= a′ |
+ a′ |
|
= |
1 |
|
|
+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
I |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
44 |
00 |
|
|
|
G13 |
|
|
|
G23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
μ |
|
+ μ |
|
|
||||||||
|
|
|
= a′ |
+ a′ |
|
|
|
|
|
μ |
13 |
|
|
|
μ |
23 |
|
|
|
|
31 |
32 |
|
||||||||
|
I |
4 |
|
= − |
|
+ |
|
|
|
= − |
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
13 |
23 |
|
|
|
|
|
E1 |
|
|
|
|
E2 |
|
|
|
|
|
|
|
|
E3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Преобразование приведенных упругих постоянных βij
βij |
= aij |
− |
ai3a j3 |
, (i, j = 1, 2, 4, 5, 6). |
|
||||
|
|
|
a33 |
|
∙Криволинейная анизотропия
Обобщенный закон Гука в криволинейной системе координат
εξ |
=a11σξ |
+ a12ση |
|
+ a13σζ + a14 |
τηζ + a15 |
τξζ + a16 |
τξη , |
||||||||||||||||||||
ε |
η |
=a |
|
σ |
ξ |
+ a |
22 |
σ |
η |
+ .................... |
............... |
+ a |
26 |
τ |
ξη |
, |
|||||||||||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
................................................................................. |
|
|
|||||||||||||||||||||||||
γ |
ξη |
=a |
16 |
σ |
ξ |
+ a |
26 |
σ |
η |
+ .................... |
.......... |
... + a |
66 |
τ |
ξη |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Обобщенный закон Гука в цилиндрической системе координат
εr |
=a11σr |
+ a12σθ |
+ a13σz + a14τθz |
+ a15τrz + a16τrθ , |
||||||||||||||||||||
ε |
θ |
=a |
12 |
σ |
r |
+ a |
22 |
σ |
θ |
+ .............................. |
.. + a |
26 |
τ |
rθ |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
................................................................................. |
||||||||||||||||||||||||
γ |
ξθ |
=a |
|
σ |
r |
+ a |
26 |
σ |
θ |
+ .............................. |
. + a |
66 |
τ |
rθ |
. |
|||||||||
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Обобщенный закон Гука в случае ортотропного тела с цилиндрической анизотропией при введении упругих характеристик – модуля Юнга и сдвига и коэффициента Пуассона
ε |
|
= |
1 |
σ |
|
− μθr σ |
θ |
− μzr σ |
|
, |
|
|
γ |
θz |
= |
|
1 |
|
|
τ |
θz |
, |
|||||||||
r |
|
r |
z |
|
|
|
|
||||||||||||||||||||||||
|
|
Er |
|
|
Eθ |
|
Ez |
|
|
|
|
|
|
Gθz |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ε |
θ |
= − μrθ σ |
|
+ |
1 |
σ |
θ |
− μzθ |
σ |
|
, γ |
|
= |
|
1 |
τ |
|
|
, |
||||||||||||
r |
|
z |
rz |
|
|
rz |
|||||||||||||||||||||||||
|
|
|
Er |
|
|
|
Eθ |
|
|
Ez |
|
|
|
|
|
|
Grz |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
μrz |
|
|
|
|
μθz |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
εθ |
= − |
|
|
|
σr |
− |
|
σz |
+ |
|
|
σz , |
γrθ = |
|
|
|
τrθ. |
||||||||||||||
Er |
|
Eθ |
Ez |
Grθ |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
81
∙ Общие уравнения теории упругости и постановка основных задач. Важнейшие вариационные принципы
Основная система уравнений равновесия в декартовой системе координат (x, y, z, t )
∂σ |
x + |
|
∂τxy |
+ |
∂τ |
xz |
+ X = 0, |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
∂y |
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
.................................................. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ a14 τ yz + a15τ xz + a16τ xy , |
||||||||
ε x =a11σ x + a12σ y + a13σz |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ a26 τxy , |
||||||
ε y =a12 σ x + a22σ y + .......... |
.......... |
|
|||||||||||||||||||||||||||||||
................................................................................. |
|||||||||||||||||||||||||||||||||
γ |
xy |
|
=a |
16 |
σ |
x |
+ a |
26 |
σ |
y |
+ .......... |
|
.......... |
........... + a |
66 |
τ |
xy |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
где X, Y, Z – |
проекции объемных сил на единицу объема. |
|
|||||||||||||||||||||||||||||||
Уравнения движения |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
∂σ |
x |
+ |
|
∂τxy |
|
+ |
∂τ |
xz + X = ρ |
∂2u |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
∂t 2 |
|
|
|
|
|
|
||||||||||||||
|
∂x |
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
.................................................. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ a12σy |
+ a13σz |
+ a14 |
τyz + a15τxz + a16τxy , |
|||||||||||||||||
εx =a11σx |
|||||||||||||||||||||||||||||||||
ε |
y |
|
=a |
|
|
σ |
x |
+ a |
|
|
σ |
y |
|
+ .......... |
.......... |
|
............ + a |
26 |
τ |
xy |
, |
||||||||||||
|
|
|
12 |
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
................................................................................. |
|||||||||||||||||||||||||||||||||
γ |
xy |
=a |
|
σ |
x |
|
+ a |
26 |
σ |
y |
+ .......... |
|
.......... |
........... + a |
|
τ |
xy |
, |
|||||||||||||||
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
66 |
|
|
||||||||||||
где ρ – плотность материала тела.
Первая основная задача. На всей поверхности задаются внешние усилия.
Граничные условия
|
cos(n, x) + τxy |
cos(n, y) + τxz cos(n, z) = X n , |
|||||
σ x |
|||||||
τxy cos(n, x) + σ y cos(n, y) + τ yz cos(n, z) = Yn , |
|||||||
τ |
cos(n, x) + τ |
yz |
cos(n, y) + σ |
z |
cos(n, z) = Z |
n |
. |
xz |
|
|
|
|
|||
Вторая основная задача. На всей поверхности задаются проекции перемещения на три несовпадающих напряжениях, например,
проекции u* , v* , w* , на оси декартовой прямоугольной системы координат. Граничные условия будут иметь вид
u = u* , v = v* , w = w* .
Смешанная задача. На части поверхности задаются усилия, а на другой части перемещения. Для случая ортотропного тела, движуще-
82
гося под действием внешних усилий, или испытывающего свободные колебания, уравнения движения в проекциях перемещения имеют такой вид:
|
|
|
∂ 2u |
|
|
∂ 2u |
|
|
|
|
∂ 2u |
|
|
∂ |
|
|
|
|
∂u |
|
|
|
|
|
|
|
|||||||||||
A44 |
|
|
|
+ A66 |
|
|
|
+ A55 |
|
|
+ |
|
|
|
|
( A11 − A44 ) |
|
+ |
|
|
|
|
|||||||||||||||
∂x |
2 |
∂y |
2 |
∂z |
2 |
|
|
|
∂x |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
+ ( A + A ) |
∂v |
|
+ ( A + A ) ∂w + X = ρ |
∂ 2u |
, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||||||||||
|
|
|
|
|
12 |
|
|
|
|
|
66 |
∂y |
|
|
|
13 |
55 |
|
|
|
|
|
|
|
∂t |
|
|
||||||||||
|
|
|
∂ 2v |
|
|
∂ 2v |
|
∂ 2 v |
|
|
∂ |
|
|
|
∂z |
|
|
|
|
|
|
|
|||||||||||||||
A |
|
+ A |
|
+ A |
+ |
|
( A + A ) ∂u |
+ |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
66 |
|
∂x |
55 |
|
∂y |
|
|
44 |
|
∂z |
|
|
|
|
|
|
|
12 |
|
66 |
∂x |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂v |
|
|
|
|
|
|
|
|
|
|
|
∂w |
|
|
|
|
∂ 2v |
|
|
||||
|
|
|
|
|
|
+ ( A22 − A55 ) |
+ ( A23 + A44 ) |
+ Y = ρ |
|
|
, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
∂y |
|
|
∂t |
2 |
|
|||||||||||||||||||||||||||
|
|
∂ |
|
w + A |
∂ |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
||||||||
A |
2 |
2 |
w + A |
2 |
w + ∂ ( A + A ) ∂u + |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
55 |
|
∂x |
2 |
44 |
|
∂y |
2 |
|
66 |
∂z |
2 |
|
|
|
|
|
|
|
13 |
|
55 |
∂x |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
+ ( A + A ) |
|
∂v |
+ ( A − A ) ∂w |
+ Z = ρ |
∂ |
2 |
w . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
23 |
|
|
|
|
44 |
|
∂y |
|
|
|
33 |
66 |
|
∂z |
|
|
|
|
|
∂t |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4.2. ПРОСТЕЙШИЕ СЛУЧАИ УПРУГОГО РАВНОВЕСИЯ
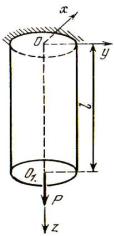
∙ Растяжение стержня под действием осевой силы и собственного веса (рис. 4.1).
Напряжения
|
|
|
P |
|
|
|
σ |
|
= |
|
, |
|
|
|
S |
|
|
|||
|
z |
|
|
= τ |
|
|
σ |
x |
= σ |
y |
yz |
||
|
|
|
|
|||
Деформации
ε |
|
= |
P |
|
a |
, |
x |
|
|||||
|
|
S |
13 |
|
||
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
ε y |
= |
|
|
a23, |
||
S |
|
|||||
|
|
|
|
|
|
|
ε |
|
= |
P |
a |
, |
|
x |
|
|||||
|
|
S |
33 |
|
||
|
|
|
|
|
|
|
= τ xz = τ xy = 0.
γ |
|
= |
|
|
P |
|
|
a |
, |
yz |
|
|
|
||||||
|
|
|
|
S |
34 |
|
|||
γ |
|
= |
|
P |
a |
, |
|||
xz |
|
|
|||||||
|
|
|
|
S |
35 |
|
|||
γ |
|
= |
P |
a . |
|||||
xy |
|
||||||||
|
|
|
|
S |
36 |
Рис. 4.1. Схема к задаче |
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
83

Перемещения
u = |
P |
|
(a x + a |
|
y + a |
|
|
x)+ ω |
|
z − ω y + u |
|
, |
||||||
|
|
|
36 |
35 |
2 |
0 |
||||||||||||
|
S |
|
|
13 |
|
|
|
|
3 |
|
||||||||
v = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
P |
(a |
|
y + a z)+ ω x − ω z + v , |
|
|
||||||||||||
|
|
|
23 |
|
|
|||||||||||||
|
S |
|
|
|
|
34 |
|
|
3 |
1 |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
w = |
P |
a z + ω y − ω x + w . |
|
|
|
|
||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
33 |
|
|
1 |
2 |
|
0 |
|
|
|
|
||||
|
|
S |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Здесь ω1 , ω2 , ω3 , |
|
u0 , ν0 , |
w0 |
– постоянные, характеризующие жест- |
||||||||||||||
кое перемещение тела в пространстве, не сопровождаемое деформациями; первые три характеризуют перемещения при повороте вокруг осей координат, а вторые три – поступательные перемещения вдоль осей.
Условия закрепленного бесконечно малого элемента на оси z около координат
u = v = w = 0, |
|
∂u |
|
|||||
|
∂u |
= |
∂v |
= |
∂v |
− |
= 0. |
|
|
|
|
|
|
||||
|
∂z |
|
∂z |
|
∂x |
|
∂y |
|
|
|
|
|
|
||||
Тогда перемещения будут
u = |
P |
(a |
x + 0,5a x), |
|||||
|
|
|||||||
|
S |
13 |
|
|
36 |
|||
|
|
|
|
|
||||
v = |
P |
(a x + a |
|
y), |
||||
|
23 |
|||||||
|
|
|
|
36 |
|
|
||
|
S |
|
|
|
) |
|||
|
|
P ( |
|
|
|
|||
w = a x + a y + a z .
35 34 33
S
В общем случае анизотропии стержень не только удлиняется в направлении силы и сокращается в поперечных направлениях, но еще испытывает сдвиги во всех плоскостях, параллельных координатным. Эти сдвиги характеризуются коэффициентами a34 , a35 , a36
|
= |
|
η |
z, yz |
= |
|
η |
yz, z |
|
|||
a34 |
|
|
|
|
, |
|||||||
Gyz |
Ez |
|||||||||||
|
|
|
|
|
|
|
||||||
|
= |
|
ηz, zx |
= |
|
ηzx, z |
|
|||||
a35 |
|
|
|
|
|
|
|
, |
||||
|
Gxz |
|
Ez |
|||||||||
|
|
|
|
|
|
|
||||||
|
= |
|
ηz, xy |
|
= |
|
ηxy, z |
. |
||||
a36 |
|
|
|
|
|
|
|
|
||||
|
Gxy |
|
|
Ez |
||||||||
|
|
|
|
|
|
|
||||||
84
Абсолютное удлинение стержня
|
f |
= |
Pla33 |
|
|
= |
Pl |
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
S |
|
|
|
|
|
|
Ez S |
|
|
|
|
Напряжения от |
|
|
|
собственного |
веса |
|
||||||||||
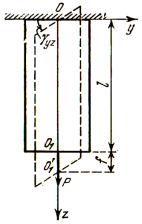
(рис. 4.2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X = Y = 0, |
Z = γ, |
|
|
|
|||||||||||
σ z = γ(l − z ), σ x = σ y = τ yz = τ xz = τ xy = 0, |
|
|||||||||||||||
где γ – удельный вес материала. |
|
|
||||||||||||||
Перемещения от собственного веса |
|
|||||||||||||||
u = γ[−0,5a |
35 |
z |
2 + (a |
|
|
x + 0,5a |
36 |
y) (l − z)], |
|
|||||||
|
|
|
|
13 |
|
|
|
|
|
|
|
|
||||
v = γ[−0,5a |
|
|
2 + (a |
|
|
|
y + 0,5a |
|
|
|||||||
34 |
z |
23 |
x) (l − z)], |
|
||||||||||||
|
|
|
|
|
|
|
|
|
36 |
|
|
|
||||
w = γ[0,5(a |
x2 + a |
|
|
y 2 + a xy) + |
|
|||||||||||
|
|
|
Рис. 4.2. Деформация |
|||||||||||||
13 |
|
|
|
23 |
|
|
|
|
36 |
|
|
|
||||
+ (a34 y + a35 x) l + 0,5a33 z (2l − z)]. |
|
стержня |
||||||||||||||
В общем случае анизотропии ось искривляется и уравнение изогнутой оси будет
x′ = −0,5γa35 z 2 , y′ = −0,5γa34 z 2 .
При этом центр нижнего конца перемещается не только вдоль z, но и в стороны, и проекции перемещения его на оси координат определяются по формулам
|
|
= −0,5γl 2a35 = −0,5γl 2 |
η |
zx, z |
|
|
||||||
f x |
|
|
, |
|||||||||
|
Ez |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= −0,5γl |
2 |
a34 = −0,5γl |
2 |
η yz, z |
|
|
||||
f y |
|
|
|
|
|
|
, |
|||||
|
|
|
Ez |
|
||||||||
|
|
|
|
|
|
1 |
|
|
||||
f |
|
= 0,5γl 2a |
|
= 0,5γl 2 |
. |
|
|
|
||||
y |
33 |
|
|
|
|
|||||||
|
|
|
|
Ez |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Если стержень закреплен так, что центр нижней поверхности остается на вертикали, то перемещение его по вертикали будет прежним
x′ = 0,5γa (lz − z2 ), |
y′ = 0,5γa (lz − z2 ). |
35 |
34 |
∙Сдвиг
Напряжения и деформации определяются по формулам (рис. 4.3)
τ yz = t, σ x = σ y = σ z = τ xz = τ xy = 0;
85

Рис. 4.3. Деформации сдвига
εε ε
x= ta14 , γ yz = ta44 ,
y= ta24 , γ xz = ta45 ,
= ta34 , γ xy = ta46 .x
Предполагая, что элемент оси z закреплен около начала координат, тогда перемещения будут
u = t (a14 x + 0,5a46 y), |
|
|||||||||
v = t (0,5a |
46 |
x + a |
24 |
y), |
|
|||||
|
|
|
|
|
|
|
|
z). |
||
w = t (a |
45 |
x + a |
44 |
y + a |
34 |
|||||
|
|
|
|
|
|
|
|
|||
Полное удлинение в направлении оси z
f |
|
= tla |
|
= tl |
η yz, z |
= tl |
ηz, yz |
. |
z |
34 |
|
|
|||||
|
|
|
Ez |
|
Gyz |
|||
|
|
|
|
|
|
|||
Объемное расширение θ , т.е. изменение единицы объема, зависит от коэффициентов взаимного влияния и определится по формулам
θ = εx + ε y + εz = t (a14 + a24 + a34 ),
или |
θ = |
t |
(η |
|
+ η |
|
+ η |
|
). |
|
x, yz |
y, yz |
z, yz |
||||||
|
|
G yz |
|
|
|
||||
|
|
|
|
|
|
|
|
||
Изменение объема всего тела
ω = tlbh (a14 + a24 + a34 ).
86
4.3. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ТЕЛА ВРАЩЕНИЯ
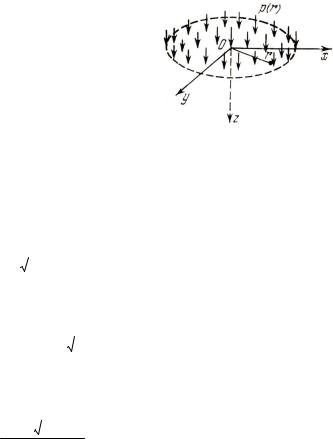
∙ Распределение напряжений в упругом полупространстве под действием осесимметричной нормальной нагрузки (рис. 4.4).
Дано упругое однородное транс- версально-изотропное полупространство, ограниченное бесконечной плоскостью с плоскостями изотропии, параллельными ограничивающей. На этой ограничивающей плоскости по площади некоторого круга распределены нормальные усилия, обладающие симметрией вращения относительно нормали, проведенной через центр круга, принимаемый за начало O
цилиндрической системы координат (ось к границе внутрь).
p(r) – интенсивность нагрузки, которая удовлетворяет условиям:
1) она конечна при всяком r; 2) в любом конечном интервале r > 0 число точек разрыва непрерывности и экстремальных точек конечно и
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) интервал ∫ρ |
|
|
|
|
|
|
|
|
|
сходится. Тогда напряжения определяются по |
||||||||||||||
|
r dr |
|||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ = − |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
∞ |
ψ(t) |
(s e−s1tz |
− s e−s2tz )tJ (tr) dt + |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(s |
− s |
|
) |
|
|
d ∫ |
||||||||||||||||||
|
r |
|
|
|
|
|
|
1 |
2 |
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
∞ |
0 |
|
|
|
|
|||||
|
|
|
|
|
|
λ |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
|
+ |
|
|
|
|
|
|
|
|
|
∫ψ(t) (s1 p2e−s1tz − s2 p1e−s2tz )tJ1(tr) dt, |
||||||||||||
|
|
s − s |
2 |
|
r |
|||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
||||
σθ = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ψ(t) (s1q2e−s1tz − s2q1e−s2tz )tJ 0 (tr) dt − |
||||||||||
(s − s |
2 |
|
)(ac − d ) |
|||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|||||||
|
|
λ |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
− |
|
|
|
|
|
|
∫ψ(t) (s1 p2e−s1tz − s2 p1e−s2tz )tJ1 (tr) dt, |
|||||||||||||||||
s − s |
2 |
|
|
r |
||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
∞ |
|
|
|
|
|||||
|
|
σz = − |
|
|
|
|
|
∫ψ(t) (s2e−s1tz − s1e−s2tz )tJ0 (tr) dt, |
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
s − s |
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|||
87

|
|
|
1 |
|
|
∞ |
ψ(t) (e−s1tz − e−s2tz )tJ1(tr) dt. |
|
τrz |
= |
|
|
|
∫ |
|||
|
|
|
|
|
||||
(s |
− s |
|
) |
|
||||
2 |
d |
|||||||
|
|
1 |
|
|
|
0 |
|
|
Здесь функция ψ(t) |
определяется по формуле |
|||||||
∞
ψ(t ) = ∫ p(ξ)ξJ0 (ξt )dξ,
0
где J0 – функция Бесселя нулевого порядка вещественного аргумента.
∙ Распределение напряжений в упругом полупространстве под действием сосредоточенной силы и произвольной нормальной нагрузки (рис. 4.5).
Распределение напряжений в трансверсально-изотропном полупространстве дается формулами
|
|
|
|
|
|
P |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
σ |
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 |
|
|
|
|
− |
|
|
|
|
|
|
|
s2 |
|
|
|
|
+ |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
r |
|
|
|
|
2π (s1 − s2 ) d |
(r |
2 + s |
|
2 z 2 )3/ 2 |
|
|
|
(r 2 |
+ s |
2 z 2 )3/ 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
λ z |
|
|
s 2 p |
|
|
|
|
|
|
|
|
|
|
s 2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
+ |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
− |
|
μ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
s1 − s2 |
|
r 2 |
|
|
|
r 2 + s 2 z 2 |
|
|
|
|
|
r 2 + s 2 z 2 |
|
|
|
|
r |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
σθ |
= − |
|
P d |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
s1 q2 |
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
s2 q1 |
|
|
|
|
|
|
− |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(r |
2 + s 2 z 2 )3/ 2 |
|
|
|
(r 2 + s2 z |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
2π ac − d s1 − s2 |
|
|
|
|
|
2 )3/ 2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
λ z |
|
|
|
|
|
s2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
s 2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
μ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
2 |
1 |
|
|
|
|
|
+ |
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
s1 |
− s2 |
|
r 2 |
|
|
|
|
|
|
r |
2 + s2 z 2 |
|
|
|
|
|
r 2 + s |
2 z 2 |
|
|
|
|
r |
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
σ z = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2π d s1 − s2 (r 2 + s12 z 2 )3/ 2 |
|
(r 2 + s22 z 2 )3/ 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
τrz |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(r 2 + s12 z 2 )3/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2π d s1 − s2 |
|
|
|
|
(r 2 + s22 z 2 )3/ 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Напряжения от силы P, приложенной не в начале координат, а в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
произвольной точке 0′ |
|
с координатами ξ, η (рис. 4.6). |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
88

Рис. 4.5. Схема к задаче
Напряжения в декартовой системе координат x, y, z
σ |
|
= |
|
1 |
(σ |
|
+ σ |
|
)+ |
|
|
|
1 |
|
|
(σ |
|
− σ |
|
) |
|
(x − ξ)2 − (y − η)2 |
, |
||||||||
x |
|
|
r |
θ |
|
|
|
r |
θ |
(x − ξ)2 + (y − η)2 |
|||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
σ |
|
|
= |
1 |
(σ |
|
+ σ |
θ |
)− |
1 |
|
(σ |
|
− σ |
θ |
) |
(x − ξ)2 − (y − η)2 |
|
, |
||||||||||||
y |
|
r |
|
|
r |
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
(x − ξ)2 + (y − η)2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ z |
= σ z , |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
τ xy = (σr − σθ ) |
|
|
(x − ξ)(y − η) |
|
, |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
(x − ξ)2 + (y − η)2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
τ xz = τrz |
|
|
|
|
|
|
|
|
|
x − ξ |
, |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
(x − ξ)2 + (y − η)2 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
τxy = τrz |
|
|
|
|
|
|
|
|
y − η |
, |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
(x − ξ)2 + (y − η)2 |
|
|
|
|||||||||||||||||
здесь σr , σθ , σ z , |
σrz |
– напряжения в цилиндрической системе. |
|||||||||||||||||||||||||||||
Пусть нагрузка распределена по некоторому участку S ограничивающей плоскости и является нормальной и заданной функцией x и y –
89

Рис. 4.6. Схема к задаче
p(x, y) (см. рис. 4.6), тогда напряжения будут определяться по другим
формулам. Пример, для σ z |
|
|
|
|
|
|
||||
|
|
|
z |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
σz = |
|
|
|
∫∫S |
|
[(x − ξ)2 |
+ (y − η)2 + s |
|
] |
− |
2π |
|
(s1 − s2 ) |
|
|||||||
d |
2 z 2 |
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
− |
|
|
|
dξdη. |
|
[(x − ξ)2 + (y − η)2 + s |
2 z 2 |
] |
|||
|
|
||||
|
|
2 |
|
|
Некоторые задачи механики неоднородных сред. Андреев В.И. (2002) рассмотрел задачи о концентрации напряжений вблизи подземного цилиндрического отверстия; осесимметричная термоупругая деформация с учетом двухмерной неоднородности материала, термонапряженное состояние массива со сферической полостью с учетом двухмерной неоднородности, расчет неоднородной в меридиальном направлении анизотропной полусферической оболочки.
Так, оболочка, армированная в кольцевом и меридиональном направлениях отличалась. Если количество арматуры на единицу площади сечения в направлении угла ϕ постоянно, то в направлении θ изменяется. Тогда E1 = E2 = const, E2 = Eθ (θ), E3 = Eϕ = const, т.е неоднородность материала будет в меридиональном направлении.
Пусть μ2 и μ3 коэффициенты армирования в направлении θ и ϕ, то модули упругости
E1 = Eв ; E2 = Ecsμ2 + Eв (1 − μ2 ); E3 = Esμ3 + Eв (1 − μ3 ).
Цытович Н.А. (1963) приводит данные Г.И. Клейна (1960), Н.Н. Иванова (1929), О.К. Фрелиха (1936) для непрерывно-неоднород- ного по глубине полупространства
90
