
ledenev-a
.pdf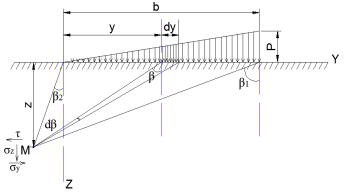
Распределение напряжений при действии нагрузки, меняющейся по закону прямоугольника (рис. 1.14) [79, 80]
σz = − |
pz |
2 |
β1 − sin |
2 |
β2 |
− tgβ2 |
|
β1 |
+ |
1 |
sin 2β1 − β2 |
− |
1 |
sin 2β2 |
|
|
|
sin |
|
|
|
|
|
; |
|||||||||
|
|
|
2 |
2 |
||||||||||||
|
πb |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
σ y |
= − |
pz |
2 |
β1 |
− 2 ln cosβ1 − cos2 β2 − 2 ln cosβ2 − tgβ2 × |
|
|||||||||||||||||
|
|
|
cos |
|
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
πb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
× β1 − |
|
sin 2β1 − β2 |
+ |
|
sin 2β |
2 |
; |
|
|
|
|
||||||||||
|
|
|
2 |
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
τ |
|
= |
|
pz |
|
[sin 2β − sin 2β |
|
+ 2(β |
|
− β ) − tgβ |
|
(cos 2β − cos 2β |
|
)]. |
||||||||||
yz |
|
|
|
2 |
2 |
2 |
2 |
|||||||||||||||||
|
|
|
2πb |
|
|
1 |
|
|
|
|
|
|
1 |
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рис. 1.14. Схема нагрузки, меняющейся по закону треугольника
Плоская контактная задача. Наряженное состояние в упругом теле в случае плоской задачи (рис. 1.15) определяется тремя компонентами напряжения: σx, σy и τ xy .
Они удовлетворяют условиям равновесия:
|
∂σ |
x |
+ |
|
∂τxy |
= 0; |
||
|
|
|
|
|
||||
∂x |
|
∂y |
||||||
|
|
|
|
|
||||
|
∂σ |
|
|
|
∂τ |
|
|
|
|
|
y |
+ |
|
|
xy |
|
= 0. |
|
∂y |
|
∂x |
|
||||
|
|
|
|
|
|
|
|
|
31

Рис. 1.15. Схема к плоской контактной задаче
Деформация упругого тела может быть выражена через относительные удлинения εx, εy и γxy, определяющиеся через u, т.е. перемещения точки упругого тела по направлению оси х и через v, т.е. перемещения по направлению оси y:
|
|
|
∂u |
|
|
|
|
||
|
= |
|
|
|
|
||||
ε x |
∂x ; |
|
|
|
|||||
|
|
|
|
∂v |
|
|
|
|
|
ε y |
|
= |
|
|
|
; |
|
|
|
|
|
∂y |
|
|
|
||||
|
|
|
|
|
|
|
∂v . |
||
λ |
|
= 1 ∂u + |
|||||||
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
2 |
∂y |
|||||||
|
|
|
|
∂x |
|||||
Так как три компоненты деформации εx, εy и γxy выражены через два компонента перемещения u и v, то между ними должно существовать некоторое соотношение
∂ 2ε x + ∂ 2ε y = 2 ∂ 2 γ xy . ∂y 2 ∂x2 ∂x∂y
Компоненты деформации связаны с компонентами напряжения соотношениями:
|
= λθ + 2με x ; |
|||
σ x |
||||
σ y |
= λθ + 2με y ; |
|||
λ |
|
= 2μγ |
xy |
, |
xy |
|
|
||
здесь θ = (ε x + ε y ) – относительное объемное расширение, а λ и μ0 – коэффициенты Ляме
λ = Eμ /(1 + μ)(1 − 2μ); μ0 = E / 2(1 + μ).
32
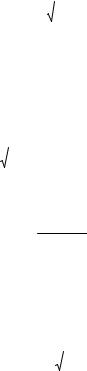
На основании этих уравнений компоненты деформации могут
быть выражены через компоненты напряжения: |
|
|||||||||||||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|||
ε x |
= |
|
|
|
|
[(1 |
− μ |
|
|
)σ x − μ(1 + μ)σ y ] ; |
||||
|
|
|
|
|
|
|||||||||
|
|
E |
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|||
ε y |
= |
|
|
|
|
|
[(1 − μ |
|
|
)σ y − μ(1 + μ)σ x |
] ; |
|||
|
|
|
|
|
|
|
||||||||
|
|
|
E |
|
|
|
|
|
|
|
||||
|
|
|
|
1 + μ |
|
|
|
|
|
|
||||
λ xy = |
|
|
|
|
|
τxy |
, |
|
||||||
|
|
|
E |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Е – модуль упругости и μ – коэффициент Пуассона.
Распределение контактных давлений под жесткими ленточными фундаментами при центральной нагрузке
p( x, y ) = |
|
2 pm |
|
, |
|
|
|
||
π 1 − ( y / b )2 |
||||
|
1 |
|
|
|
где pm – среднее давление на единицу площади подошвы фундамента; y – расстояние по горизонтали от середины фундамента до рассматриваемой точки; b1 – полуширина фундамента.
Распределение контактных давлений под жесткими ленточными фундаментами при внецентренной нагрузке
|
|
|
|
|
P |
|
|
|
|
|
2ey |
|
2qb |
|
|
|
p |
( x, y) |
= |
|
|
|
|
|
|
|
|
1 + |
|
− |
1 |
|
+ q , |
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
π b |
|
− y |
|
|
|
|
|
|
P |
|
|
|||
|
|
|
2 |
2 |
|
|
|
|
b1 |
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
где P – сосредоточенная сила; e – |
|
эксцентриситет; b1 – полуширина |
||||||||||||||
ленточного фундамента; q – интенсивность боковой пригрузки.
tgβ = 4 (1− μ2 ) Pe , 2πEb13
E и μ – модуль деформаций и коэффициент бокового расширения грунтового массива.
Распределение контактных давлений по подошве сооружений конечной жесткости
Wξ,η = |
1 |
|
(1− μ02 ) |
∫∫ |
|
p(ξ, η) dξdη |
|
, |
|
|
|
|
|
||||
|
|
|
|
|||||
|
π π F |
(x − ξ)2 + ( y − η)2 |
||||||
где Wξ,η – осадка точки поверхности грунта с координатами ξ и η; p(ξ, η) – неизвестное распределение реактивных давлений.
33
1.2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ
|
Декартовы координаты (x, y, z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂σ |
x + |
∂τxy |
|
+ |
∂τ |
xz |
+ X |
= 0; |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
∂z |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂τxy |
+ |
|
|
∂σ y |
|
|
+ |
∂τ yz |
+ Y = 0; |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
∂z |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂τ |
xz + |
|
∂τ yz |
|
|
+ |
|
∂σ |
z |
+ Z |
= 0. |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
∂z |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Цилиндрические координаты (τ, θ, z) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂σr + |
1 |
|
∂τrθ |
|
|
+ |
|
∂τrz |
|
+ σr − σθ + R = 0; |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
r |
|
|
|
|
∂θ |
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂τrθ + |
1 |
|
|
|
∂σθ |
|
|
+ |
|
∂τθz |
+ |
|
2τrθ |
+ Θ = 0; |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
r |
|
|
|
|
∂θ |
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂τrz + |
1 |
|
|
|
|
∂τθz |
+ |
|
|
∂σz + |
τrz |
+ Z = 0. |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
r |
|
|
|
|
∂θ |
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Сферические координаты (τ, θ, ϕ) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
∂σr |
+ |
1 |
|
|
∂τrθ |
+ |
|
|
|
1 |
|
|
|
|
|
|
|
∂τrϕ |
+ |
1 |
[2σ |
|
|
− (σ |
θ |
+ σ |
ϕ |
) + τ |
rθ |
ctgθ]+ R = 0; |
|||||||||||||||||||||||||||||
|
∂r |
|
|
|
|
|
∂θ |
r sin ϕ |
|
|
|
|
∂ϕ |
|
|
|
|
|
r |
|
||||||||||||||||||||||||||||||||||||||||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
∂σrθ + |
1 |
|
∂σθ + |
|
|
1 |
|
|
|
|
|
|
|
∂τθϕ |
+ |
1 |
[3τ |
rθ |
+ (σ |
θ |
− σ |
ϕ |
) ctgθ]+ Θ = 0; |
||||||||||||||||||||||||||||||||||||
r |
r sin ϕ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂r |
|
|
|
|
∂θ |
|
|
|
|
|
|
∂ϕ |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
∂τrϕ |
+ |
1 |
|
|
∂τθϕ |
+ |
1 |
|
∂σϕ |
|
|
+ |
1 |
(3τrϕ + 2τθϕctgθ)+ Φ = 0. |
|
||||||||||||||||||||||||||||||||||||||||||||
|
∂r |
r |
|
r |
|
∂ϕ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂θ |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
В соотношениях X, Y, Z, R, Θ, Φ – |
|
|
|
компоненты объемной силы. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1.3. ТЕНЗОРЫ И ИНВАРИАНТЫ НАПРЯЖЕНИЙ
Обозначения приняты из книги Н.Н. Малинина (1975).
Напряженное состояние в точке – совокупность нормальных и касательных напряжений, действуюших по всем площадкам, содержащим данную точку (рис. 1.16).
Тензор напряжений – симметричная квадратная матрица
|
σ x |
τxy |
τxz |
|
|
σ x |
τxy |
τxz |
|
σ1 |
0 |
0 |
||||
Τ = |
τxy |
σ y |
τ yz |
; |
Τ = |
. |
σ |
y |
τ |
; |
Τ = |
. |
σ |
2 |
0 |
. |
σ |
|
|
|
|
σ |
|
|
|
yz |
σ |
|
|
|
|
||
|
|
τzy |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
τzx |
σ z |
|
. |
|
σ z |
|
. . |
σ3 |
|||||||
34
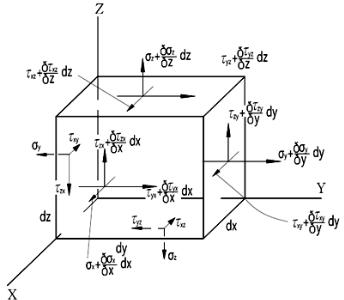
Рис. 1.16. Напряженное состояние элемента тела
Октаэдрические напряжения
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
= |
1 |
|
(σ + σ |
|
+ σ |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
окт |
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Главные нормальные напряжения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
σ = |
1 |
(σ + σ |
|
); |
|
σ |
|
|
= |
1 |
(σ |
|
|
+ σ |
|
|
); σ |
|
|
|
= |
1 |
(σ |
|
+ σ ). |
|||||||||||||||||||||||||
|
|
2 |
|
23 |
|
|
2 |
3 |
31 |
|
3 |
|||||||||||||||||||||||||||||||||||||||
|
12 |
2 |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Главные касательные напряжения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
τ = ± |
1 |
(σ − σ |
|
); |
|
τ |
|
|
= ± |
1 |
(σ |
|
− σ |
|
|
); τ |
|
|
= ± |
1 |
(σ |
|
− σ ). |
|||||||||||||||||||||||||||
|
2 |
|
23 |
|
2 |
3 |
31 |
|
3 |
|||||||||||||||||||||||||||||||||||||||||
12 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Среднее объемное напряжение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
σ |
|
= |
1 |
(σ + σ |
|
+ σ |
|
) = |
1 |
(σ |
|
+ σ |
|
|
|
+ σ |
|
). |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
ср |
|
2 |
3 |
|
x |
y |
z |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тензор напряжений можно разложить на шаровой тензор и девиатор напряжений
35
|
|
|
|
|
|
|
|
|
|
Тσ = Тσ0 |
+ Dσ , |
|
|
|
s0 |
0 |
|
0 |
|
|
|
|
|
|
|||
где Тσ0 |
|
|
s0 |
|
0 |
|
|
шаровой тензор напряжений; |
|||||
= 0 |
|
– |
|||||||||||
|
|
0 |
0 |
|
s0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
- s0 |
|
|
t1x |
|
|
tzx |
|
|
||
|
sx |
|
|
|
|
|
|
||||||
Dσ = |
txy |
|
s y |
- s0 |
tzy |
– девиатор напряжений. |
|||||||
|
|
txz |
|
|
tyz |
|
|
|
|
|
|||
|
|
|
|
|
|
sz - s0 |
|
||||||
Компоненты девитора напряжений представляют в виде |
|||||||||||||
|
|
|
|
|
|
|
|
|
sij = sij - sij s0 , |
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sij |
|
|
1 |
|
|
1, |
если i = j, |
|
|
|
s0 |
= |
|
|
|
- |
|
dij sij ; dij |
= |
если i ¹ j; |
|
|
|
|
3 |
|
3 |
||||||||
|
|
|
|
|
|
|
|
|
0, |
||||
|
|
|
sx = sx - s0 , s y = sy - s0 , sz = sz - s0 ; |
||||||||||
|
|
|
|
|
sxy |
|
= txy , |
s yz = tyz , szx |
= txz . |
||||
Сумма нормальных напряжений в координатных плоскостях равна нулю
sx + s y + sz = 0.
Главные напряжения (на взаимно перпендикулярных площадках, на которых касательные напряжения равны нулю) являются корнями кубического уравнения
|
|
|
|
s3 - j (Т |
σ |
) s2 - j |
2 |
(Т |
σ |
) s - j |
2 |
(Т |
σ |
) = 0 ; |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
j1 (Тσ ) = sx + s y + sz ; |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
j2 (Тσ ) = -sx s y - s y sz - sz sx + t2xy + t2yz + t2zx ; |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
tyx |
tzx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
sx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
j (Т |
σ |
) = t |
|
s |
|
t |
|
|
= s |
s |
|
s |
|
- s |
|
t2 |
- s |
|
t2 |
- s |
t2 |
+ 2t |
|
t |
|
t |
|
||||||||
3 |
|
xy |
|
y |
|
zy |
|
|
x |
|
y |
|
|
z |
|
|
|
x |
yz |
|
|
|
y |
|
zx |
z |
xy |
|
xy |
|
yz |
|
zx |
||
|
|
|
|
tyz |
sz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
txz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
36

или
j1 (Тσ ) = σii ; j2 (Тσ ) = 1 [(σii2 ) − σij σij ];
2
|
|
|
|
|
|
|
|
|
j3 (Тσ ) = |
1 |
σii σik σkl |
+ |
1 |
(σii )3 − |
1 |
(σii ) σij σij . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Инварианты тензора напряжений через главные напряжения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j1 (Тσ ) = σ1 + σ2 + σ3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j2 (Тσ ) = −σ1σ2 − σ2σ3 − σ3σ1 ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j3 (Тσ ) = σ1σ2σ3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Инварианты девиатора напряжений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j1 (Dσ ) = 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
j |
|
(D ) = |
1 |
[(σ |
|
|
− σ |
|
)2 |
+ (σ |
|
− σ |
|
)2 |
|
+ (σ |
|
− σ |
|
|
|
)2 + 6 (τ2 |
+ τ2 |
+ τ2 |
)]; |
|||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
x |
y |
y |
z |
z |
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
σ |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
yz |
zx |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
x |
− σ |
0 |
|
|
|
|
|
|
τ |
yx |
|
|
|
|
|
|
|
|
|
|
τ |
zx |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j3 (Т |
|
τxy |
|
|
|
|
|
|
σ y − σ0 |
|
|
|
|
|
|
|
|
τzy |
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
xz |
|
|
|
|
|
|
|
|
|
|
τ |
yz |
|
|
|
|
|
σ |
z |
− σ |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||||
|
|
В тензорной записи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
(D ) = |
1 |
|
s |
|
s |
|
|
|
; |
|
|
j |
|
|
(D ) = |
1 |
s |
|
|
s |
|
s |
|
. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
σ |
|
|
2 |
|
|
ij |
|
ij |
|
|
|
|
|
|
|
|
3 |
|
|
σ |
|
|
|
3 |
|
|
|
ij |
|
ik |
|
|
kb |
|
|
|
|
|
|
|
|||||||||||
|
|
Интенсивность напряжений (нормальных) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
σ |
|
= |
|
|
|
|
|
|
= |
|
T = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(σ |
|
− σ |
|
|
)2 |
|
+ (σ |
|
|
− σ |
|
|
|
)2 |
+ |
|
||||||||||||||||||||||||||||||||
|
|
i |
3 j |
2 |
(D ) |
3 |
|
|
x |
y |
|
y |
z |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
+ (σ |
|
− σ |
|
|
)2 |
+ 6 |
(τ2 |
|
|
+ τ2 |
|
+ τ2 |
) = |
|
|
|
|
3 |
s |
|
|
s = |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
yz |
|
|
|
zx |
|
|
|
|
|
|
|
|
|
|
1 |
|
ij |
ij |
|
|
|
|
|
|
|
||||||||
|
|
|
|
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(σ − σ |
2 |
)2 |
+ (σ |
2 |
|
− σ |
3 |
)2 |
+ (σ |
3 |
|
− σ )2 |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
При чистом сдвиге σ1 = τ, σ2 = 0, |
|
σ3 = −τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
σi = 
 3 τ.
3 τ.
По А. Надаи (1954) интенсивность напряжений пропорциональна октаэдрическому касательному напряжению
37

τ |
|
= |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
(σ − σ |
0 |
)2 + (σ |
2 |
− σ |
0 |
)2 |
+ (σ |
3 |
− σ |
0 |
)2 . |
|
|
|||||||||||||
|
|
|
||||||||||||||||||||||||||
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При τxy = τ yz = 0 (плоская задача) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
σ |
|
= |
σ x + σ y |
± |
1 |
|
|
|
|
|
|
|
, σ |
|
|
= σ |
|
|
||||||||||
|
|
(σ |
x |
− σ |
y |
) |
2 + 4τ2 |
3 |
z |
. |
||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
1, 2 |
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Инварианты девиатора напряжений при преобразовании координатных осей.
Дифференциальные уравнения равновесия Коши. Напряжения на выделеном элементе показаны на рис. 1.16.
Уравнения равновесия имеют вид
|
|
|
∂σ |
+ |
|
∂τxy |
+ |
∂τ |
xz |
+ Rx = 0; |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
∂x |
|
|
∂y |
|
∂z |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A = πr |
2 |
|
∂τxy |
+ |
|
∂σ y |
+ |
|
∂τ yz |
+ Ry |
= 0; |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
∂x |
|
∂y |
|
|
|
|
∂z |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
∂τzx |
+ |
|
|
∂τxy |
+ |
|
∂σz |
+ R |
|
= 0. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∂x |
|
|
|
∂y |
|
|
|
|
∂z |
|
z |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Учет разрыва сплошности упругого основания. Применение уравнений теории урпугости для расчета оснований заглубленных фундаментов (например, Р. Миндлина) приводит к погрешности, связанной с тем, что грунтовое основание почти не сопротивляется растяжению. Упругая среда в равной степени сопротивляется как растяжению, так и сжатию. Одними из первых это учитывали М.И. Горбу- нов-Посадов и О.Я. Шехтер (1963).
Приведем результаты решения С.В. Босакова (1986) задачи об изгибе стержня в упругом полупространстве с учетом разрыва сплошности основания. Рашение выполнено методом Б.Н. Жемочкина (1948, 1962). Использована также идея итерационного расчета пространственного клина при заданных воздействиях на его гранях (Я.С. Уф-
лянд, 1972) .
Получены выражения для расчета перемещений границы клина в виде упругого четвертьпространства от действия горизонтальнной силы на границе (рис. 1.17)
|
P(1− ν2 ) |
1 |
|
1 |
|
1 |
|
∞ |
|
1 |
|
τ2 |
|
|
|
|
|||||
V (r, z) = |
|
|
0 |
|
|
+ |
|
+ |
|
|
|
∫ |
1 |
+ |
|
|
|
P− |
1 |
+iτ |
(chμ) dτ ; |
πE |
|
|
R |
R |
|
|
|
chπτ |
C(τ) |
||||||||||||
|
|
|
|
||||||||||||||||||
|
0 |
|
|
|
|
|
ar |
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
2 |
|
|
0 |
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
38
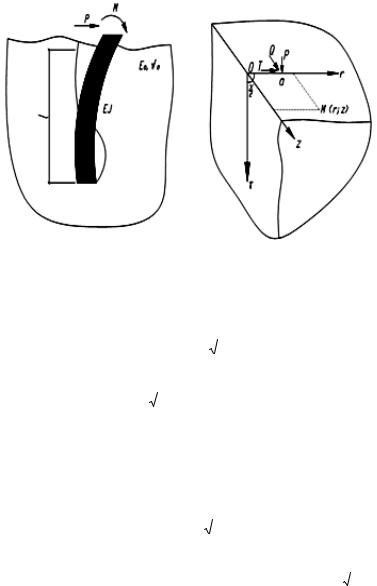
a) |
б) |
Рис. 1.17. Схема нагружения изгибаемого стержня (а) и пространственного клина с приложенными сосредоточенными силами (б)
|
|
|
|
|
|
|
P(1+ ν |
0 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ 1 |
|
∞ τ thπτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
U (r, z) = |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
− 4ν |
0 |
|
− r |
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
P |
|
(chμ) dτ; |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2πE0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂r ar |
|
|
|
C(τ) |
|
− |
1 |
+iτ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
W (r, z) = − |
P(1 + ν |
0 |
) |
r |
∂ ∞ τthπτ |
P |
|
|
|
|
(chμ) dτ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
2πE0 |
|
|
|
|
|
|
|
∂z ∫0 C(τ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ar |
|
|
|
|
|
− |
|
|
+iτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
U (r, z) = |
Ta(1 + ν ) |
|
|
|
|
∂ 1 |
|
+ |
|
1 |
+ |
|
T (1 + ν ) |
|
3 − 4ν0 − r |
|
∂ |
|
× |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
2πE0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πE0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂r R1 |
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
T (1 + ν |
0 |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
× |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 − 4ν0 − r |
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πE0 |
|
|
|
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
τ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dτ |
|
|
||||||||||||||||||||
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
− |
− |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
(chμ) |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
a |
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
1 |
|
|
|
|
|
|
|
; |
|||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2z |
|
|
|
|
|
|
|
|
(a + r) |
|
|
|
|
|
|
|
R |
2 |
|
|
|
|
|
|
|
ar |
0 |
chπτ |
|
− |
|
+iτ |
|
|
|
|
|
C(τ) |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
U (r, z) = |
|
Qz(1+ ν ) |
|
|
∂ 1 |
|
+ |
|
1 |
− |
Qa(1+ ν ) |
|
|
|
− 4ν0 |
− r |
|
∂ |
|
1 |
|
× |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2πE0 |
|
|
|
|
|
|
∂r R1 |
|
|
|
|
R2 |
|
|
|
|
|
|
2πE0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂r |
ar |
|
||||||||||||||||||||||||||||||||
|
|
|
|
∂ ∞ |
|
|
|
|
|
sh |
π |
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
× |
|
|
|
|
∫thπτ |
|
|
|
|
|
|
|
|
P− |
1 |
+iτ (chμ) dτ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
∂z |
|
C(τ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
39

W (r, z) = |
Q(1+ ν ) |
− 4ν0 |
− z |
|
∂ 1 |
+ |
|
1 |
− |
Q(1 + ν ) |
× |
|||||||||||||||||
|
|
|
|
|
0 |
3 |
|
|
|
|
|
|
|
|
|
0 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πE0 |
|
|
|
|
π |
|
|
∂z R1 |
|
|
R2 |
|
|
|
4πE0 |
|
|
|||||||||
|
|
|
|
|
∂ 2 |
∞ |
|
sh |
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
× |
|
ar |
∫thπτ |
|
|
P− |
1 |
+iτ (chμ) ; |
|
|
|
|
|
|
||||||||||||||
|
∂z 2 |
C(τ) |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
C(τ) = sh2 |
π |
τ − τ2 ; |
chμ = |
a 2 + r 2 + z 2 |
; |
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2ar |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
R = |
(r − a)2 + z 2 |
; |
|
R = |
(r + a)2 + z 2 |
, |
|
|
||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где V, U, W – перемещения граней четвертьпространства в направлении осей γ, r, z (см. рис. 1.17); P, T, Q – сосредоточенные силы, приложенные к грани четвертьпространства в точке a; E0 , ν0 – модуль уп-
ругости и коэффициент Пуассона материала клина; r, z – точки грани,
где определяется перемещение; P− |
1 |
+iτ (chμ) – функция Лежандра. |
|
||
2 |
|
|
Полупространство со стержнем образовано из двух четвертьпространств, соединенных между собой контактом в отдельных точках по методу Б.Н. Жемочкина. В каждой точке контакта действуют три связи, соответствующие нормальным и касательным напряжениям.
Перемещения вершины стержня на уровне поверхности полупро-
странства можно записать в виде |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|||
|
|
u0 = kuP |
|
; u0 = kuM |
|
|
|
P |
|
|
; |
|
||||
|
|
|
E0l 2 |
|||||||||||||
|
|
|
|
E0l |
|
|
|
|
||||||||
|
|
|
|
P |
|
|
|
|
|
|
|
|||||
|
|
ϕ0 = kϕP |
|
ϕ0 = kϕM |
|
|
|
P |
|
|
|
|||||
|
|
|
; |
|
|
|
|
|
|
|
, |
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
E0l 2 |
|
|
|
E0l 2 |
|||||||||
где P, |
|
– внешняя нагрузка на стержень ( см. рис. 1.17); u0, ϕ0 – ли- |
||||||||||||||
P |
||||||||||||||||
нейное и угловое перемещения стержня поверхности попупространства; l – длина стержня; kuP , kϕP , kuM , kϕM – безразмерные коэффициенты
для определения перемещения, находимые из решения системы канонических уравнений смешанного метода. В случае действия единичных сил их значения приведены в таблице для некоторых показателей
гибкости β = E0l 4 / El , где Еl – изгибная жесткость стержня, ν0 = 0,3ub / l = 0,1 (b – ширина стержня). По теореме о взаимности перемещений kuM = kϕp , поэтому их значения объединены.
40
