
ledenev-a
.pdfПоведение стареющих материалов (бетонов) описывается теорией наследственного старения или теорией упругоползучего тела. Стареющие и нестареющие среды называют вязкоупругими.
Решение квазистатических задач с постоянной областью контакта осуществляется применением принципа Вольтерра. Рассматриваются функции интегральных операторов Вольтерра, например, t
t
H *y (t) = ∫ H (t, τ) y(τ) dτ,
τ
где H (t, τ) – ядро.
Связь между напряжениями и деформациями наследственноупругого тела при простом растяжении– сжатии представляется формулами:
|
|
|
t |
|
= Et ε(t) ; |
|
σ(t) = E0 ε(t) − ∫ |
0 |
Г(t − τ) ε(τ) dτ |
||||
|
|
|
|
|
|
|
−1 |
|
1 |
|
−1 |
σ(t), |
|
ε(t) = E0 |
σ(t) − ∫ |
|
K (t − τ) σ(τ) dτ |
= Et |
||
|
|
0 |
|
|
|
|
где E0 – мгновенный модуль упругости; K (t − τ) – ядро ползучести
(последействия); Г(t) и K(t) – функции, определяемые из опытов. Контактные напряжения возникают при вдавливании штампа в
однородное изотропное вязкоупругое полупространство при фиксированной области контакта
ρ(x, y, t) = |
|
Et |
p0 |
(x, y) f (t), |
|
− ϑ2 |
|||
1 |
|
|
||
|
|
t |
|
|
где p0 (x, y) – функция распределения напряжений под штампом в
случае идеально упругого полупространства.
Уравнение ползучести бетона получено Н.Х. Арутюняном (1952)
|
|
ε(t) = σ(t) / E(t) − ∫τt |
K (t, τ) σ(τ) dτ, |
||
|
|
|
|
1 |
|
где K (t, τ) = |
∂ |
δ (t, τ) ; δ(t, τ) = |
1 |
+ C(t, τ) ; E(τ) – мгновенный мо- |
|
∂τ |
|
||||
|
|
E(τ) |
|
||
дуль упругости, зависящий от τ; С(t, τ) – мера ползучести – деформация ползучести в возрасте (τ) от напряжения единой интенсивности.
191

Контактные задачи теории идеально жесткопластических тел.
Возможна и другая формулировка – « Технологические задачи теории пластичности». Здесь имеется в виду проблема обработки металла давлением.
Приведем уравнения плоского течения: уравнения равновесия
∂σ |
x + |
∂τxy |
= 0; |
∂τxy |
+ |
∂σ y |
= 0 , |
|
∂y |
∂x |
∂y |
||||
∂x |
|
|
|
||||
условие текучести
(σ x − σ y )2 + 4τ xy 2 = 4x2 ,
условие соосности главных осей тензора напряжений и скоростей деформации
|
|
|
|
∂υy |
|
∂υ |
x |
|
|
|
∂υ |
x |
|
(σ |
x |
− σ |
y |
) |
|
+ |
|
|
= 2τ |
|
|
||
|
|
|
|
|
|||||||||
|
|
|
∂x |
|
∂y |
|
|
xy |
∂x |
||||
|
|
|
|
|
|
|
|
|
|||||
условие несжимаемости
|
∂υ |
x |
|
∂υ y |
|
|
|
|
+ |
|
|
= 0 . |
|
|
∂x |
∂y |
|
|||
|
|
|
|
|||
∂υ + y , ∂y
Система является гиперболической, имеет два семейства ортогональных характеристик (α, β). Сетка характеристик совпадает с сет-
кой траекторий максимальных касательных напряжений (линий скольжения).
Угол наклона характеристик семейства α к оси абсцисс
ϕ= 1 arctg σ y − σx . 2 2τxy
Нормальные напряжения на характеристиках одинаковы и равны среднему напряжению в точке
q = − σ x + σ y , k
где q – среднее безразмерное давление. В идеально пластическом теле
σx |
/ k |
= −q M sin 2ϕ; τxy / k = cos 2ϕ. |
||
σ |
|
/ k |
|
|
y |
|
|
||
|
|
|
||
192
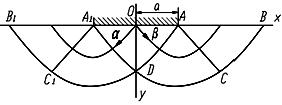
Рис. 8.5. Схема к задаче Прандтля
Давление штампов на полупространство. Классическая пло-
ская задача Прандтля (1948). Это задача о начальном течении жесткопластической полуплоскости от давления плоского штампа длиной 2а. От действия штампа материал стремится выпучиться вдоль свободных участков границы полуплоскости (рис. 8.5).
Контактная поверхность абсолютно гладкая при движении штампа вниз с постоянной скоростью.
Выделим характерные области: ABCDC1B1A1A – область пластического состояния материала; АВ(А1В1) – свободная граница, на которой σ y = τxy = 0; АВС(А1В1С1) – равномерное напряженное состояние
σx = τxy = 0; σ y = −2k; |
ADA1 – равномерное напряженное состояние |
материала σx = −kπ, σ y |
= −k(2 + π), τxy = 0 . |
В итоге, предельное давление
σ y = −k(2 + π) ,
предельная нагрузка
P = −2ak(2 + τ) .
Контактная задача с управляющими параметрами для жесткого штампа на упругом слое переменной толщины. Модель упруго-
го слоя применяется в решениях многочисленных прикладных контактных задач геомеханики. Наиболее полно методика решения таких задач разработана для предельного случая, когда слой с достаточной степенью приближения может быть заменен упругим полупространством.
Рассмотрим однородный невесомый упругий континуум D в форме пространственного клина 0 ≤ x < ∞, − ∞ < y < ∞, 0 ≤ z ≤ xtgα
с центральным углом при ребре 0 < α < 90°. Наклонная плоскость S1, ограничивающая D снизу, является защемленной. На горизонтальную поверхность клина S2 в пределах конечной области F передается давление ρ(ξ, η) от подошвы штампа Ω. В случае отрыва части штампа от
193
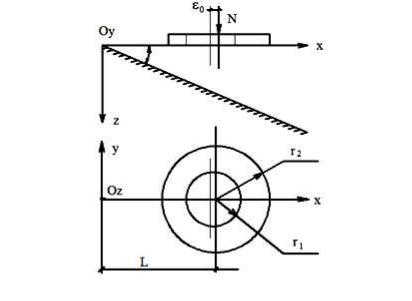
основания F < W, при отсутствии отрыва F ≡ Ω (рис. 8.6 – 8.8). Континуум D характеризуется модулем деформации Е и коэффициентом Пуассона n (С.М. Алейников, С.В. Иконин, 1990).
Сформулированной контактной задаче отвечает следующая система интегральных уравнений:
∫∫w(x, y, x, h)r(x, n) dxdh = Wc + jx (x - xc ) + jy ( y - yc );
Ω
∫∫r(x, h) dxdh = N ;
Ω
∫∫r(x, h) xdxdh = Nxc ;
Ω
∫∫r(x, h) hdxdh = Nyc ; r(x, h) ³ 0,
Ω
где в качестве фундаментального решения w(х, у, ξ, h) используется приближенный алгебраический аналог; Wc – осадка штампа в точке с координатами хс, ус, где приложена равнодействующая вертикальная нагрузка N; jх, jу – соответственно крены штампа в направлении осей Ох, Оу. Ограничение r(x, h) ³ 0 связано с отсутствием растягивающих
напряжений под подошвой штампа.
Рис. 8.6. Расчетная схема для эксцентричного кольцевого фундамента
194

Рис. 8.7. Расчетная схема для трапециевидного фундамента
Рис. 8.8. Расчетная схема для квадратного фундамента с эксцентричной нагрузкой
Решение этой системы выполняется прямым методом граничных элементов в предположении кусочно-постоянной аппроксимации контактных давлений ρ(ξ, η) . В качестве точек коллокации выбираются
центры тяжести контактных элементов. При этом соответствующий алгебраический аналог системы принимает вид:
195
n |
|
∑r j dij - jx (xi - xc ) - jy ( yi - yc ) - wc = 0, (i =1, n); |
|
i=0 |
|
|
|
n |
n |
∑r j DSi = N , |
∑r j Dsi x j = Nxc ; |
j=0 |
j =0 |
n
∑r j Dsi y j = Nyc , r j ³ 0.
i=0
Здесь неизвестными являются контактные давления pj в пределах граничных элементов, осадка штампа Wc и крены jх, jу. Число граничных элементов в общем случае равно п, площадь j-го элемента ∆sj, а координаты его центра тяжести – хj, уj. Коэффициенты канонических уравнений вычисляются по формуле
dij = ∫∫w(xi , yi , x, h) dxdh ,
Ωi
где w(x j , y j , x, h – осадка точки (x, h) Î W j от единичной верти-
кальной силы, приложенной к поверхности клина S2 в точке (xi, yi). При решении второй системы из-за ограничения r j ³ 0 в случа-
ях, когда наблюдается отрыв штампа от основания, требуется перестроить исходную расчетную схему путем удаления из области элементов, где условие r j ³ 0 не выполняется. Это эквивалентно вычер-
киванию из матрицы системы строк и столбцов, отвечающих удаляемым элементам. Опыт расчетов показывает, что, как правило, при отрыве штампа от основания для выяснения фактической области контакта F необходимы 3 – 6 итераций, на каждой из которых система после усечения решается заново.
Рассмотренная вторая система алгебраических уравнений с ограничениями и подход к ее решению положены в основу методики предотвращения крена y штампов на упругом слое переменной толщины. Первый вариант методики предполагает поиск управляющего параметра n, обеспечивающего целенаправленное изменение формы штампа в соответствии с направлением изменения сжимаемости основания – вдоль оси Ох. Параметру n с некоторым шагом придаются конкретные числовые значения, которым отвечают штампы различной формы в плане, но одинаковые по площади. Для каждого значения ν решается система. В результате, получается набор таблично заданных значений функции j(n). Решая j(n) = 0, находим значение управляющего пара-
196
метра, соответствующего такой геометрической форме подошвы штампа в плане, при которой у него отсутствует крен.
Суть второго варианта заключается в том, что при заданных форме, расположении и размерах штампа равнодействующая вертикальной нагрузки смещается в плане в точку, необходимую для обеспечения равномерности осадки основания под штампом. При этом вторая система уравнений существенно упрощается и принимает вид
|
n |
|
|
∑r j dij -Wc = 0, i =1, n; |
|||
j =1 |
|||
|
n |
||
∑r j DS j = N; |
|||
|
|
|
|
j =1 |
|||
|
n |
||
∑r j Ds j x j + Nex = Nxc ;
j =1n
∑r j DS j y j + Ney =Nyc ; p j ³ 0,
i=1
где неизвестными являются pj, Wc – управляющие параметры ex, eу, представляющие собой искомые величины смещения силы N относительно точки (xc, yc) соответственно вдоль осей Ох и Оу. То обстоятельство, что управляющие параметры в явном виде вошли в систему, позволяет значительно ускорить их определение. Так, если под штампом отсутствует зона отрыва, решение задачи ограничивается одной итерацией.
Оба предложенных подхода были апробированы в численных экспериментах на ЭВМ. На примере кольцевого штампа показано, как с помощью изменения формы штампа можно добиться его равномерной осадки на слое переменной толщины. Принятая при решении данной задачи расчетная схема приведена на (см. рис. 8.6). Отсутствие крена у штампа достигалось путем смещения внутренней окружности кольца на величину u = e0 .
Влияние технологии работ на НДС оснований, зданий и со-
оружений. Ильичевым В.А. (2008) рассмотрена плоская задача о контактных напряжениях и форме контактной поверхности абсолютно жесткого штампа в процессе наращивания его длины lx (t). Собственный вес штампа при бетонировании – q(x). Под штампом образуется эпюра прогиба y(x, t). Скорость фронта бетонирования Vδ (t). Высота фундамента постоянна.
197
Штамп непрерывно растет слева направо со скоростью
= 0, t < tT
VT (t ) Vb (t - tT ), t ³ tT ;
t
Lb (t) = ∫0Vb (t) dt, 0 < t < tbf ;
|
0, |
t < t |
T |
|
|
|
|
lт (t) = |
∫0tVt (t)dt, t ³ tT , |
||
|
|
|
|
где lb (t) – длина забетонированного участка; lт (t) – длина штампа в твердом состоянии; tb t – время окончания бетонирования фундамента.
Вертикальные перемещения точек поверхности определяются по формуле
b |
(t ) |
|
||
L |
|
|
||
|
∫ |
q(x) K (x - x) dx, t < tT ; |
||
|
|
|
||
|
0 |
|
|
|
L т (t ) |
Lb(t ) |
|||
y(x, t) = |
∫ p(x, t) K (x - x) dx + ∫q(x) K (x - x) dx, tT £ t < tbf ; |
|||
|
0 |
|
LT (t ) |
|
LT (t) |
L |
|||
|
∫ p(x, t) K (x - x) dx + ∫q(x) K (x - x) dx, tbf £ t. |
|||
|
0 |
|
LT (t ) |
|
Контактные напряжения p(x, t) и перемещения штампа y(x, t) при
tT £ t £ tbf |
определяют из системы уравнений |
|
|
|
|||||||||
|
|
LT (t ) |
|
|
|
|
L b (t) |
|
|
|
|
||
y(x, y) = ∫ p(x, t) K (x - x) dx + ∫ q(x) K (x - x) dx; |
|||||||||||||
|
|
|
0 |
|
|
|
|
LT (t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶y(x, t) |
||||
¶y(x, t) |
|
¶y(0, t) |
|
x |
¶y(x, t) |
|
|
|
|||||
|
= |
+ |
|
= LT |
(t) - |
||||||||
|
|
|
|
|
|
|
x |
|
; |
||||
|
|
|
|
|
|||||||||
|
¶t |
|
¶t |
|
|
lT (t) |
¶(t) |
|
|
|
¶t |
||
LT (t ) |
|
|
L т (t ) |
|
|
|
|
|
|
|
|
||
|
∫ p(x, t) dx = ∫ q(x) dx; |
|
|
|
|
|
|
||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
LT (t ) |
|
|
LT (t ) |
|
|
|
|
|
|
|
|||
|
∫ xp(x, t) dx = ∫xq(x) dx. |
|
|
|
|
||||||||
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
198

Рис. 8.9. Характер эпюр контактных давлений:
1 – по М.А. Садовскому; 2 – по М.И. Горбунову-Посадову; 3 – по И.Я. Штаерману; 4 – по Н.Ф. Кокосимиди; 5 – по Е. Шульцу;
6 – по В.М. Кириллову; 7 – по СНиП 2.02.02–85 методом внецентренного сжатия; 8 – по СНиП 2.02.02–85 методом экспериментальных эпюр;
9 – опыты (К.Ф. Кокосимиди)
Первое уравнение описывает контактную задачу с учетом перегрузки; второе – скорость поступательного и вращательного перемещений штампа; третье и четвертое – условия равновесия сил и моментов.
Приведены примеры расчетов при разных схемах устройства фундаментов (слева-направо, из середины к краям, от краев к середине).
На рисунке 8.10 приведены (В.И. Кириллов, 1992) экспериментальные и теоретические эпюры нормальных контактных напряжений под подошвой незаглубленного жесткого штампа.
8.5.ПРОГНОЗ СКОРОСТИ ОСАДОК
ИНАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ НЕОДНОРОДНЫХ ОСНОВАНИЙ ТЯЖЕЛЫХ СООРУЖЕНИЙ
Решение выполнено Н.Н. Леонтьевым и Х.Ш. Тураевым (1991). Уравнения состояния упругого неоднородно-ползучего основания
в условиях плоской деформации определяются соотношениями:
σx (t)
σy (t)
= |
|
N (x, y, t) |
|
∂u(t) |
|
|
|
|
|
∂x |
|
1 |
|
||||
|
− v2 (z, y) |
||||
= |
|
N (x, y, t) |
|
∂v(t) |
|
|
|
|
|
|
|
1 |
|
∂y |
|||
|
− v2 (z, y) |
||||
+ v(x, y) |
∂v(t) |
|
∂y |
||
|
+ v(x, y) ∂u(t)
∂x
;
;
199
τxy (t) = τ yx (t) = |
|
|
N (x, y, t) |
∂u(t) |
+ |
∂v(t) |
||||||||||||||
|
|
|
|
|
|
|
|
|
∂y |
, |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2[1 + v(x, y)] |
|
∂x |
|||||||||||
где |
N (x, y, t) = E(x, y, τ) (1 + R ); |
|
||||||||||||||||||
|
|
|||||||||||||||||||
R * f = |
1 |
|
|
|
∫ |
t |
R(x, y, t, τ) E(x, y, t) f (τ) dτ. |
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
E(x, y, |
τ) |
|
||||||||||||||||||
|
|
|
τ1 |
|
|
|
|
|
|
|
|
|
|
|||||||
Здесь R(x, y, t, τ) – резольвента ядра K (x, |
y, t, τ) ; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
1 |
|
|
|
|
|||
R(x, y, t, z) = −E(x, y, t) |
|
|
|
|
|
|
|
+ C(x, y, t, τ) ; |
||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
∂τ F (x, y, t) |
|
|
||||||||
E(x, y, t) = |
|
Eep (x, y, t) |
, Eep (x, y, t) > 0; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
− v 2 (x, t) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
v(x, y) = |
|
vep |
(x, |
y) |
, |
|
0 < vep (x, y) ≤ 0,5. |
|||||||||||||
|
− vep (x, y) |
|
||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||
Здесь Eep (x, y, t), C(x, y, t, τ), vep (x, |
y) – |
модуль деформации, мера |
||||||||||||||||||
ползучести и коэффициент Пуассона упругого неоднородно-ползучего грунта.
Полагают, что основание представляет собой сжимаемый слой толщиной H, расположенный на бесконечно жестком массиве, и работающий в условиях плоской деформации. Выражения работы всех внешних и внутренних сил полосы шириной dx = 1 и высотой H, выделенной из того слоя-основания на возможных для нее m + n перемещениях
∫∂σ x (t) / ∂xϕ j dF − ∫ τxy (t) ϕ′j dF + ∫ p(x, |
y, t) ϕ j dy = 0, ( j = 1, 2, 3, ..., m); |
|
∫∂τ xy (t) / ∂xψ h dF − ∫σ y (t) ψ′h dF + ∫ q(x, |
y, t) ψ h dy = 0, (h = 1, 2, 3, ..., n). |
|
Известные перемещения некоторой точки M (x, y) основания |
||
|
m |
n |
u(x, y, t) = ∑Ui (x, t) ϕi ( y) ; v(x, y, t) = ∑Vk (x, t) ϕk ( y) , |
||
|
i=1 |
k =1 |
где Ui (x, t) и |
Vk (x, t) – неизвестные обобщенные перемещения; |
|
ϕi ( y) и ϕk ( y) – |
известные безразмерные функции, характеризующие |
|
поперечное распределение перемещений основания.
200
