
УПП Физическая химия 260800.62
.pdf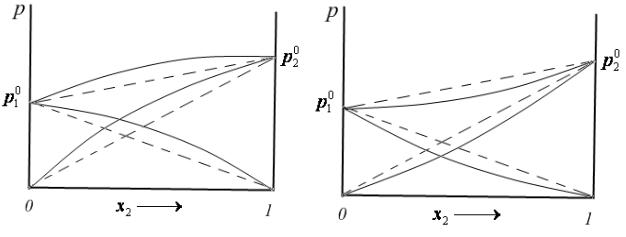
В предельно разбавленных растворах к растворенному веществу закон Рауля не применим. В этом случае зависимость парциального давления пара растворенного вещества от его мольной доли в растворе описывается законом Генри.
Закон Генри: парциальное давление пара растворенного вещества
над предельно разбавленным раствором пропорционально его мольной доле:
P2 = K2x2 |
(151) |
где P2 –давление насыщенного пара растворенного вещества над раствором; х2 – мольная доля растворенного вещества; К2 – постоянная Генри.
Уравнение Генри имеет большое практическое значение для изучения растворимости газов в растворах.
Для неидеальных растворов наблюдаются отклонения от закона Рауля, различные как по величине, так и по знаку.
Если при образовании раствора притяжение между молекулами становится меньше, чем в чистых веществах, то молекулы из раствора переходят в пар легче, чем из чистых жидкостей. В этом случае наблюдаются положительные отклонения от закона Рауля (рис.10). Примером такого раствора является система вода – 1,4-диоксан.
Если при образовании раствора силы притяжения между молекулами увеличиваются, наблюдаются отрицательные отклонения от закона Рауля (рис. 11). Например, раствор вода - серная кислота.
Рис. 10. Положительные отклонения |
Рис. 11. Отрицательные отклонения |
от закона Рауля |
от закона Рауля |
Каждая жидкость при нагревании до определенной температуры начинает кипеть. Кипение – это процесс парообразования во всем объеме жидкости в отличие от испарения, при котором парообразование идет только от поверхности. Испарение идет при любых температурах, кипение же
61

происходит только при той температуре, при которой давление насыщенного пара, образующегося в жидкости, достигает величины внешнего давления. Это относится как к чистым жидкостям, так и к растворам. Однако между понятиями «температура кипения чистого жидкого вещества» (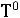 ) и «температура кипения раствора» (
) и «температура кипения раствора» (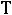 ) существует разница. Чистое жидкое вещество (жидкость), сколько бы ни кипела, состава не изменяет и кипит при постоянной температуре. При кипении же раствора состав раствора изменяется, что влечет за собой изменение его температуры кипения. Температура кипения раствора нелетучего вещества всегда выше температуры кипения чистого растворителя, и тем выше, чем выше концентрация нелетучего растворенного вещества:
) существует разница. Чистое жидкое вещество (жидкость), сколько бы ни кипела, состава не изменяет и кипит при постоянной температуре. При кипении же раствора состав раствора изменяется, что влечет за собой изменение его температуры кипения. Температура кипения раствора нелетучего вещества всегда выше температуры кипения чистого растворителя, и тем выше, чем выше концентрация нелетучего растворенного вещества:
> |
(152) |
Для идеальных и предельно разбавленных растворов неэлектролитов между концентрацией раствора и повышением температуры его кипения существует связь:
|
|
= Е·m |
(153) |
|
где: |
- |
– повышение температуры кипения (разность |
||
между температурами кипения раствора |
и чистого растворителя |
); |
||
Е – эбуллиоскопическая постоянная; m – концентрация раствора, выраженная через моляльность.
Температура кипения раствора нелетучего вещества всегда выше температуры кипения чистого растворителя, и тем выше, чем выше
концентрация нелетучего растворенного вещества: |
|
||||||
|
Е = |
|
|
(154) |
|
|
|
|
|
|
|||||
где R – универсальная газовая постоянная; |
– температура |
кипения |
|||||
чистого растворителя; M1 – молярная масса чистого растворителя; |
– |
||||||
теплота кипения чистого растворителя. |
|
|
|
|
|||
Каждый растворитель имеет свою эбуллиоскопическую постоянную. |
|||||||
|
|
|
|
|
|
Таблица 8. |
|
Эбуллиоскопические постоянные некоторых жидкостей |
|
||||||
|
|
|
|
|
|
|
|
|
Жидкость |
|
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
Вода |
|
|
0,52 |
|
|
|
|
Метиловый спирт |
|
|
0,84 |
|
|
|
|
Этиловый спирт |
|
|
1,2 |
|
|
|
|
Ацетон |
|
|
1,48 |
|
|
|
|
Бензол |
|
|
2,64 |
|
|
|
|
Хлороформ |
|
|
3,76 |
|
|
|
Уравнения 153 и 154 позволяют рассчитать молярную массу растворенного вещества:
62

М2=Е |
|
(155) |
|
где М2 – молярная масса растворенного вещества; Е – эбуллиоскопическая постоянная; g1 – масса растворителя; g2 – масса растворенного вещества, 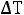 – повышение температуры кипения растворителя над раствором.
– повышение температуры кипения растворителя над раствором.
Температура замерзания раствора (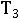 ), содержащего нелетучее растворенное вещество, всегда ниже температуры замерзания чистого растворителя (
), содержащего нелетучее растворенное вещество, всегда ниже температуры замерзания чистого растворителя (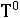 )
)
< |
(156) |
Понижение температуры замерзания идеальных и предельно разбавленных растворов неэлектролитов пропорционально их концентрации:
(157)
где 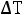
 =
= 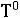

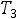 – понижение температуры замерзания (разность между температурами замерзания чистого растворителя и раствора ); К – криоскопическая постоянная; m – концентрация раствора, выраженная через моляльность.
– понижение температуры замерзания (разность между температурами замерзания чистого растворителя и раствора ); К – криоскопическая постоянная; m – концентрация раствора, выраженная через моляльность.
Криоскопическую постоянную ассоциируют с молярным понижением температуры замерзания. Она показывает, насколько понижается температура замерзания в результате растворения одного моля нелетучего растворенного вещества в 1000 г растворителя. Криоскопическая постоянная зависит только от свойств растворителя и не зависит от свойств растворенного вещества:
К = |
|
(158) |
|
где: R – универсальная газовая постоянная; 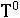 – температура замерзания чистого растворителя; M1 – молярная масса чистого растворителя;
– температура замерзания чистого растворителя; M1 – молярная масса чистого растворителя; 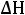
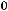 – теплота плавления чистого растворителя.
– теплота плавления чистого растворителя.
Каждый растворитель имеет свою криоскопическую постоянную. Таблица 9.
Криоскопические постоянные некоторых жидкостей
Жидкость |
Е |
Вода |
1,86 |
Бензол |
5,12 |
Уксусная кислота |
3,81 |
Фенол |
6,81 |
Нафталин |
7,14 |
Уравнения 157 и 158 позволяют определить молярную массу растворенного вещества:
63

|
М2=К |
|
|
(159) |
|
|
|
||
где: М2 |
– молярная масса растворенного вещества; К – |
|||
криоскопическая |
постоянная; g1 |
– масса растворителя; g2 – масса |
||
растворенного вещества, 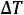
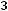 – понижение температуры замерзания.
– понижение температуры замерзания.
5.5. Диффузия и осмотическое давление раствора
Диффузия - это самопроизвольный процесс выпаривания растворенного вещества в объеме системы.
Скорость диффузии растворенного вещества:
ν= - DS |
|
|
, |
|
(160) |
||
|
|
||||||
где: S – площадь диффузии; |
|
|
- |
градиент концентрации; D - |
|||
|
|||||||
коэффициент диффузии. |
|
|
|
|
|
|
|
Коэффициент диффузии зависти от свойств раствора и размеров |
|||||||
частиц: |
|
|
|
|
|
|
|
D = |
|
|
, |
(161) |
|||
|
|
||||||
где η – вязкость растворителя; 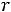 – радиус диффундирующих частиц.
– радиус диффундирующих частиц.
Чем больше молекулярная масса диффундирующего вещества, тем медленнее оно диффундирует. Например, для мочевины (М = 60 г/моль), D = 110, глицерина (М = 92 г/моль), D = 73, сахарозы (М = 342 г/моль), D = 38, для яичного альбумина (М = 43800 г/моль), D = 7,7.
Диффузия будет наблюдаться и в тех случаях, если в растворе будет находиться мембрана, проницаемая как для молекул растворителя, так и для молекул растворенного вещества.
Осмос – это самопроизвольное проникновение растворителя в раствор, отделенный от него полупроницаемой перегородкой, через которую может поступать растворитель, но не может проходить растворенное вещество. Количественной характеристикой осмоса является осмотическое давление.
Рис. 12. Осмотическое давление
64

Осмотическое давление – это избыточное давление, которое нужно приложить к раствору, чтобы прекратился осмос, и в системе установилось равновесие. Осмотическое давление раствора пропорционально его концентрации и температуре и не зависит ни от природы растворенного вещества, ни от природы растворителя. Величина осмотического давления определяется по уравнению Вант-Гоффа:
или |
, (162) |
где: π – осмотическое давление раствора; С – молярная концентрация раствора; R – универсальная газовая постоянная; Т – температура раствора, i – изотоничеcкий коэффициент Вант-Гоффа.
Уравнение справедливо для идеальных и предельно разбавленных растворов неэлектролитов. Уравнение Вант-Гоффа позволяет определить молярную массу растворенного вещества:
М2 = |
|
(163) |
|
где М2 – молярная масса растворенного вещества; g1, ρ1– масса и плотность растворителя; g2 – масса растворенного вещества, π – осмотическое давление раствора.
Контрольные вопросы
1.Растворы и их термодинамическая классификация по взаимодействию между компонентами.
2.Термодинамическое условие самопроизвольного образования истинного раствора при постоянных р и Т.
3.Аддитивные и не аддитивные экстенсивные величины.
4.Парциальные молярные величины. Определение и примеры таких величин. Что такое «идеальный раствор»?
5.Химический потенциал, активность и коэффициент активности компонента смеси.
6.Химический потенциал компонента идеального раствора и его зависимость от состава раствора.
7.В чем причина положительных и отрицательных отклонений от закона Рауля?
8.Дайте определение бесконечно разбавленным растворам.
9.Сформулируйте законы Коновалова.
10.Опишите способы определения молекулярной массы растворенного вещества.
11.Закон Генри, коэффициент Генри, его физический смысл.
12.Растворимость газов в жидкостях.
13.Давление насыщенного пара над раствором. Закон Рауля.
14.Сформулируйте и запишите математические выражения закона Рауля.
15.Влияние ассоциации молекул растворенного нелетучего вещества на давление насыщенного пара растворителя.
65
16.Растворимость неэлектролитов в растворах электролитов.
17.Почему давление насыщенного пара растворителя над идеальным раствором меньше, чем над чистым растворителем?
18.Закон Рауля, его графическая интерпретация для идеального раствора, образованного двумя летучими взаимно растворимыми жидкими компонентами.
19.Эбулиоскопическое следствие закона Рауля, его графическая интерпретация.
20.Криоскопическое следствие закона Рауля, его графическая интерпретация.
21.Диаграмма зависимости давления пара от температуры для воды и для разбавленных водных растворов. Влияние растворѐнного вещества на диаграмму.
22.Осмотическое давление растворов и уравнение Вант Гоффа.
23.Коллигативные свойства растворов.
24.Неидеальные растворы, активность, способы еѐ выражения.
25. Причины положительных и отрицательных отклонений от закона Рауля.
Тема 6. ЭЛЕКТРОХИМИЯ
Различают две основные группы проводников электрического тока: проводники первого рода, электрическая проводимость которых обусловлена электронами и проводники второго рода, обладающие ионной проводимостью. Вещества, проводящие электрический ток, называются электролитами. Электролиты – химические соединения, полностью либо частично диссоциирующие на ионы в растворе.
Согласно теории Аррениуса электролиты при растворении диссоциируют на положительно (катионы) и отрицательно (анионы) заряженные ионы. Причина электролитической диссоциации заключается во взаимодействии молекул растворяемого вещества и растворителя.
Электролиты при растворении могут диссоциировать на ионы полностью или частично. Для характеристики полноты диссоциации электролита Аррениус ввел понятие степени диссоциации (α) – отношение числа молекул электролита, распавшихся в растворе на ионы, к первоначальному числу его молекул в растворе. Степень диссоциации электролита в растворе зависит от его природы, концентрации, природы растворителя, температуры и присутствия посторонних электролитов.
Все электролиты условно делят на сильные и слабые.
Сильные электролиты в растворах диссоциируют практически полностью (α ≈ 1). К ним относятся вещества, у которых связи между частицами преимущественно электростатические (соли, сильные кислоты и основания, например HCl, HNO3, H2SO4, NaOH, KOH, NaCl, K2SO4 и др.).
Слабые электролиты — вещества с преимущественно ковалентными связями (большинство органических веществ – CH3COOH, пиридин, некоторые неорганические кислоты и основания – H2CO3, H3PO4, H2S,
66

NH4OH и др.). Слабые электролиты диссоциируют частично и в растворе устанавливается динамическое равновесие между ионами и недиссоциированными молекулами.
Равновесие, которое устанавливается в растворе слабого электролита между ионами и молекулами, можно описать, применяя законы химического равновесия, и в конечном итоге рассчитать для константы равновесия. Например, для диссоциации типичного слабого электролита – раствора уксусной кислоты:
CH3COOH = Н+ + CH3COO-
константа равновесия, выраженная через молярные концентрации реагентов (Ci), имеет вид:
К = |
|
(164) |
|
Константа равновесия процесса диссоциации слабого электролита называется константой диссоциации (КД). Величина КД зависит от природы электролита и растворителя, а также от температуры, и характеризует способность данного электролита распадаться на ионы в растворе. Чем больше КД, тем легче и полнее диссоциирует электролит в растворе.
Многоосновные кислоты и основания диссоциируют ступенчато, каждая из ступеней характеризуется своей константой диссоциации. Для одновалентного электролита связь между константой и степенью диссоциации электролита выражает закон разбавления Оствальда:
К = 
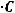 , (165)
, (165)
где: C – молярная концентрация электролита, моль/л; 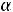 – степень диссоциации электролита.
– степень диссоциации электролита.
6.1. Ионное произведение воды. рН раствора
Вода является слабым электролитом и частично диссоциирует на ионы Н+ и ОН- и по реакции:
Н2О 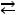 Н+ + ОН-.
Н+ + ОН-.
В водных растворах концентрации ионов Н+ и ОН-связаны между собой через константу диссоциации воды:
К = 
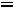


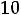

 .
.
Концентрация недиссоциированных молекул воды в растворе практически постоянна и равна:
[Н2О] = 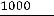


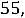
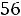
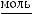

Произведение ионов Н+ и ОН- является постоянной величиной для
данной температуры и называется ионным произведением воды (КW):
КW = [H+]·[OH-] = K·[Н2О] = 1,8·10-16·55,56 = 1·10-14,
КW = [H+]·[OH-] = 1·10-14.
67

Ионное произведение воды, согласно закону действующих масс, является константой, не зависит от концентрации ионов водорода и гидроксид-ионов и постоянно при данной температуре.
Ионное произведение воды – весьма важная величина, так как позволяет для любого водного раствора найти концентрацию ионов водорода при известной концентрации гидроксид-ионов и наоборот. В чистой воде или нейтральном растворе:
[H+] = [OH-] = 

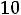

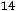 = 1·10-7 моль/л.
= 1·10-7 моль/л.
Вкислой среде [H+] > 1·10-7 моль/л.
Вщелочной среде [H+] < 1·10-7 моль/л.
Для удобства обычно пользуются не концентрациями [H+] и [OH-], а отрицательными их логарифмами, обозначаемыми символами рН и рОН:
рН = - 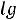
 ; рОН = -
; рОН = - 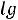
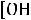

 .
.
Для водных растворов выполняется соотношение:
рН + рОН = 14.
Тогда: |
|
в нейтральной среде |
рН = 7 |
в кислой среде |
рН < 7 |
в щелочной среде |
рН > 7 |
6.2. Электрическая проводимость растворов электролитов
Электрическая проводимость (L) – это способность вещества проводить электрический ток под действием внешнего электрического поля. По физическому смыслу это – величина, обратная сопротивлению (R):
L= |
|
|
|
(166) |
|
|
где ρ – удельное сопротивление, Ом/м; S – поперечное сечение проводника, м2; l – длина проводника, м.
Различают удельную и молярную электрические проводимости растворов электролитов.
Удельная электрическая проводимость (κ) – электрическая проводимость объема раствора, заключенного между двумя параллельными электродами площадью 1 м2, расположенными на расстоянии 1 м друг от друга. Удельная электрическая проводимость является величиной, обратной
удельному сопротивлению: |
|
κ = |
(167) |
Единицs измерения удельной электрической проводимости - Ом-1м-1 =
См/м (См - сименс).
В электрохимии часто пользуются традиционным определением удельной электрической проводимости - это электрическая проводимость
столбика вещества длиной 1 см и с сечением 1 см2, при этом размерность
Ом-1см-1 = См/см.
68

|
|
|
|
Удельная |
электрическая |
||||||
|
|
|
|
проводимость |
|
электролитов |
|||||
|
|
|
|
определяется |
количеством |
|
и |
||||
|
|
|
|
зарядом |
ионов, |
переносящих |
|||||
|
|
|
|
электричество, а также скоростью |
|||||||
|
|
|
|
их движения в электрическом поле. |
|||||||
|
|
|
|
График |
зависимости |
κ |
от |
||||
|
|
|
|
концентрации |
|
раствора |
для |
||||
|
|
|
|
сильных |
|
|
электролитов |
||||
|
|
|
|
представляет собой кривую с четко |
|||||||
|
|
|
|
выраженным максимумом, а для |
|||||||
|
|
|
|
слабых – этот максимум в |
|||||||
|
|
|
|
значительной |
степени |
размыт |
и |
||||
Рис. 13 Зависимость удельной |
практически не проявляется (рис. |
||||||||||
13) |
|
|
|
|
|
|
|||||
электрической проводимости сильных |
|
области |
малых |
||||||||
и |
слабых |
электролитов |
от |
В |
|
||||||
концентраций растворов сильных и |
|||||||||||
концентрации раствора |
|
||||||||||
|
слабых |
электролитов |
рост |
||||||||
|
|
|
|
||||||||
электрической проводимости обусловлен увеличением количества ионов, переносящих электричество.
При увеличении концентрации увеличивается плотность раствора, что снижает скорость движения ионов, при этом у слабых электролитов заметно снижается степень диссоциации. Поэтому κ для умеренно слабых электролитов начинает уменьшаться в области значительно более разбавленных растворов и роста электропроводности практически не наблюдается, а максимум на кривой получается очень пологим. Повышение температуры на 1 К увеличивает удельную электропроводность на 2–2,5 % для сильных электролитов за счет понижения вязкости раствора и уплотнения гидратированных ионов, а для растворов слабых электролитов – за счет увеличения степени диссоциации в случае эндотермической реакции, происходит при растворении электролита. На величину удельной электрической проводимости, кроме перечисленных факторов, влияет валентность (заряд) иона: чем больше заряд иона, тем большее количество электричества он переносит.
Молярная электрическая проводимость (λ) – электрическая проводимость объема раствора электролита, содержащего 1 моль-эквивалент растворенного вещества, находящегося между двумя параллельными электродами, расположенными на расстоянии 1 м друг от друга. Единицей измерения молярной электрической проводимости является См·м2/моль.
Удельная и молярная электрические проводимости связаны между
собой соотношением: |
|
|
λ = |
κ, |
(168) |
69

где С – молярная концентрация растворенного вещества, моль/л; λ – молярная электрическая проводимость, См·м2/моль; κ – удельная электрическая проводимость, См/м.
Зависимость λ от скорости движения для одновалентных ионов выражается уравнением:
λ = α·F·(u+ + u-) (169),
где: u+ и u- – абсолютные скорости движения положительных и отрицательных ионов соответственно, α – степень диссоциации электролита, F – постоянная Фарадея.
Для сильных электролитов можно принять α = 1, поэтому
λ = F(u+ + u-) |
(170) |
Произведения λ+ = Fu+ и λ- = Fu- называются подвижностями ионов:
λ∞ = λ+ + λ- |
(171) |
Для предельно разбавленных растворов (С→0, α→1) справедливо равенство:
λ∞ = |
(172) |
где: 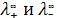 - подвижности ионов при предельном (бесконечном) разведении, являющиеся специфическими величинами для ионов; λ∞ - электрическая проводимость гипотетического бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами.
- подвижности ионов при предельном (бесконечном) разведении, являющиеся специфическими величинами для ионов; λ∞ - электрическая проводимость гипотетического бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами.
Уравнение 172 справедливо как для сильных, так и для слабых электролитов и называется законом независимого движения ионов Кольрауша (законом аддитивности электрической проводимости). Согласно этому закону, молярная электрическая проводимость при предельном
разведении равна сумме подвижностей ионов при предельном разведении.
Численные значения подвижностей ионов и в настоящее время оценены практически для всех ионов и приводятся в справочниках. Например, пользуясь справочными данными, молярную электрическую проводимость предельно разбавленного раствора уксусной кислоты можно определить:
λ∞ = 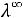
 +
+ 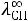
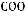
 = 349,8 + 40,9 = 390,7 См·см2/моль
= 349,8 + 40,9 = 390,7 См·см2/моль
Сравнение численных значений λ∞ для различных ионов показывает, что аномально высокими величинами электрических проводимостей в водном растворе обладают ионы гидроксония Н3О+ и гидроксила ОН- . Это объясняется эстафетным механизмом перемещения указанных ионов в растворе. Поэтому растворы кислот и щелочей по сравнению с растворами солей при одинаковых концентрациях обладают большей электрической проводимостью.
В разбавленных растворах слабых электролитов электрическое взаимодействие между ионами мало, поэтому:
70
