
- •ВВЕДЕНИЕ
- •ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- •Постановка задачи
- •Приближенные (итерационные) методы решения НАУ
- •Метод деления отрезка пополам (дихотомии).
- •Метод простой итерации
- •Метод релаксации
- •Метод Ньютона (касательных)
- •Метод хорд
- •МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- •Постановка задачи
- •Прямые методы решения СЛАУ
- •Метод Крамера
- •Метод обратной матрицы
- •Метод Гаусса
- •Метод прогонки
- •Итерационные методы решения линейных алгебраических систем
- •Метод простой итерации
- •Метод Якоби
- •Метод Гаусса-Зейделя
- •АППРОКСИМАЦИЯ ФУНКЦИЙ
- •Постановка задачи интерполяции
- •Локальная интерполяция
- •Кусочно-постоянная интерполяция
- •Кусочно-линейная интерполяция
- •Кубический интерполяционный сплайн
- •Глобальная интерполяция
- •Полином Лагранжа
- •Подбор эмпирических формул
- •Метод наименьших квадратов
- •ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- •Постановка задачи
- •Формулы прямоугольников
- •Формула трапеций
- •Формула Симпсона
- •ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- •Постановка задачи
- •Приближенные методы решения задачи Коши для ОДУ первого порядка
- •Метод Эйлера
- •Модифицированный метод Эйлера
- •Методы Рунге-Кутты
- •Численные методы решения систем ОДУ первого порядка
- •МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ДЛЯ ОДУ
- •Постановка задачи
- •Аппроксимация производных
- •ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ И РЕКОМЕНДАЦИИ К ЭКЗАМЕНУ
Метод релаксации
На практике часто в качестве функции x выбирают
функцию |
|
|
x x cf x , |
где |
c |
– |
|
|
некоторая |
постоянная. |
|||||||||||||||||||||||||||||||||||||||
Постоянную |
|
|
|
|
|
|
c |
|
|
|
выбирают |
таким |
образом, чтобы |
условие |
|||||||||||||||||||||||||||||||||||
|
|
|
|
q |
1 |
|
выполнялось бы для всех x a,b . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
При таком выборе функции x метод простой итерации |
|||||||||||||||||||||||||||||||||||||||||||||
называют методом релаксации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Получим условия на выбор константы c : |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
cf |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
x |
|
|
|
|
x |
1 cf |
x |
1 2 cf x 0 |
|
|||||||||||||||||||||||||||||||||||||||
Таким образом, |
|
если |
|
|
f |
|
|
|
то |
|
|
|
2 |
|
|
c 0 . |
Если |
же |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
x 0 , |
|
f |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
c 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
f x 0 , то |
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Отсюда видно, что знак постоянной c совпадает со знаком |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
производной |
|
|
|
|
f |
|
|
|
|
Часто |
c |
берут в виде: c M m , |
где |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x . |
||||||||||||||||||||||||||||||||||||||||||||
M max f |
|
|
x , |
m min f |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Убедимся, |
|
что |
|
такой |
выбор |
c |
|
удовлетворяет |
условию |
|||||||||||||||||||||||||||||||||||||||
сходимости. |
|
|
|
|
Пусть |
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
M 0 |
и |
m 0 , |
и, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
x 0 . Тогда |
||||||||||||||||||||||||||||||||||||||||||
следовательно, |
c 0 и |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 M m f |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , т.к. |
M f x . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
|
|
|
M m |
|
|
|
|
|
|
f x M m |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Следовательно, |
|
|
|
2 |
|
|
|
|
c 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пусть теперь |
f |
|
|
|
|
|
|
|
|
|
M |
0 , |
m 0 |
c 0 и |
||||||||||||||||||||||||||||||||||
|
|
x 0 . Тогда |
|||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 f |
x M m |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , т.к. |
|
|
|
|
|
|
|||||||
|
|
M m |
|
|
f |
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x M m |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
f x M m 0, f |
|
x M 0 и m 0 . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
14
Следовательно, |
2 |
|
|
c 0 . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
f x |
|
|
|
|
|
|
|
|
||
ПРИМЕР 1.3. |
Найдем |
с |
точностью 0,001 |
второй |
||||||||||
корень уравнения |
|
f x x3 |
6x2 |
3x 11 0 , |
лежащий |
на |
||||||||
интервале |
1, 3 . |
Для |
определения |
значения |
параметра |
c |
||||||||
необходимо |
найти |
максимальное |
и |
минимальное значения |
||||||||||
производной функции |
f |
|
|
на |
отрезке 1,3 . Для |
этого |
||||||||
x |
||||||||||||||
необходимо |
найти |
значения |
f |
|
на концах интервала и |
в |
||||||||
x |
||||||||||||||
точках экстремума, |
где |
f |
|
|
|
(если эти точки лежат |
на |
|||||||
x 0 |
||||||||||||||
исследуемом отрезке). Далее среди этих значений выбираются
максимальное и минимальное. В нашем случае |
|
|
|||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
f x 3x |
12x |
|
3 , |
f 1 3 12 3 6 |
|
|||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
|
f |
|
36 3 6 |
, f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 27 |
|
x 6x 12 0 при x 2 |
||||||||||||||||||||||||||||
|
Экстремум |
|
производной |
находится |
на |
заданном |
отрезке |
||||||||||||||||||||||||
1, 3 , |
находим |
значение |
|
производной |
в |
этой |
точке: |
||||||||||||||||||||||||
|
|
|
|
3 9 . Следовательно |
|
|
|
|
|
|
|
||||||||||||||||||||
f |
2 12 24 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
M max 6, 6, 9 6 , |
m min 6, 6, 9 9 , |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
c |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
2 |
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
M m |
|
6 |
9 |
15 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Таким образом, x x |
|
2 |
|
x3 |
6x2 |
3x 11 . |
|
|||||||||||||||||||||||
|
15 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 3 |
|
|
|||||||
|
Выберем начальное приближение x0 |
|
2 , |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
следующие приближения вычисляются по формуле |
|
|||||||||||||||||||||||||||||
|
|
xk 1 xk |
|
2 |
|
|
|
xk |
3 6xk |
2 |
|
3xk 11 , k=0, 1, 2,.. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Условием окончания итерационного процесса является |
||||||||||||||||||||||||||||||
|
условие: |
|
xk 1 |
xk |
|
0,001 или |
|
|
f xk |
|
|
0,001 |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
15

Результаты вычислений оформим на рабочем листе Excel в виде таблицы:
|
A |
B |
|
C |
||
1 |
Номер |
xk |
|
xk 1 xk |
|
|
|
|
|
||||
|
итерации |
|
|
|
||
|
|
|
||||
2 |
0 |
2 |
|
|
|
|
3 |
1 |
2,133333 |
0,133333 |
|
|
|
4 |
2 |
2,106983 |
0,026351 |
|
|
|
5 |
3 |
2,1121 |
0,005117 |
|
|
|
6 |
4 |
2,111101 |
0,000999 |
|
|
|
7 |
5 |
2,111296 |
0,000195 |
|
|
|
Здесь формулы для вычисления x1 имеют вид:
=B2+2/15*(B2^3-6*B2^2+3*B2+11), а для x1 x0 :
=ABS(B3-B2). Остальные вычисления получаются простым копированием формул.
Метод Ньютона (касательных)
Для уравнений (1.1) метод Ньютона определяется формулой:
f xk . Суть метода состоит в замене нелинейной f xk
функции f(x) линейной. Геометрическая иллюстрация метода |
|||
представлена на рис. 1.5. Участок кривой |
y f x на отрезке |
||
x xk , xk 1 |
заменяется отрезком касательной, проведенной из |
||
точки xk |
к графику функции y f x . Уравнение касательной |
||
имеет |
вид |
y f xk x xk f xk . |
Найдем точку |
пересечения касательной с графиком функции y 0 , т.е. с осью
абсцисс, и обозначим ее |
xk 1 . Тогда уравнение касательной в |
||
этой точке будет иметь вид |
0 f xk xk 1 xk f xk . |
||
Отсюда можно найти xk 1 |
xk |
f xk |
|
|
. |
||
f xk |
|||
16
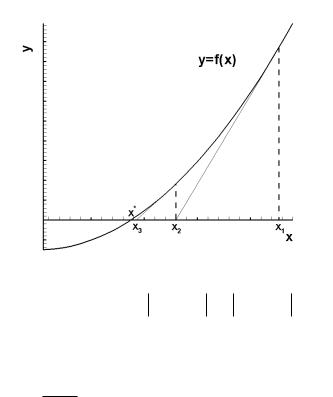
Рис. 1.5. Графическая интерпретация метода Ньютона
Можно показать, что xk 1 x* q xk 1 x* 2 , т.е. метод
сходится со вторым порядком.
Метод Ньютона можно трактовать как метод простой итерации, если функцию x выбрать в виде
x x ff xx .
Замечание. Если известен интервал изоляции, в котором f x не меняет знак, то в качестве начального приближения
берут тот конец интервала изоляции, для которого знаки f x
и |
|
|
|
|
|
|
f x совпадают. |
|
|
|
|||
|
ПРИМЕР 1.4. Найдем с помощью метода Ньютона третий |
|||||
корень |
уравнения |
x3 6x2 3x 11 0 , |
лежащий на |
|||
интервале |
4,5 , с точностью 0,001 . Сначала убедимся, что |
|||||
f |
|
не |
меняет |
знака |
на этом отрезке. |
|
x |
f x 6x 12 |
|||||
f |
|
|
при x 2 , т.е. |
|
|
|
x 0 |
f x 0 на интервале [4,5]. Так как |
|||||
|
|
|
|
|
|
17 |

f 5 1 0 , |
то на этом конце знаки |
f x |
|
|
|
|
|
|
|
||||
|
и f x совпадают |
||||||||||||
и x0 5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисления оформим в виде таблицы: |
|
|
|
|
|
|
|
||||||
Номер итерации |
|
xk |
f xk |
|
f xk |
|
xk 1 xk |
|
|
||||
|
|
|
|||||||||||
|
|
|
|||||||||||
0 |
|
|
5 |
1 |
|
|
|
18 |
|
|
|
|
|
1 |
|
|
4.944444 |
0.027606 |
17.00926 |
|
0.055556 |
|
|
||||
2 |
|
|
4.942821 |
2.33E-05 |
16.98059 |
|
0.001623 |
|
|
||||
3 |
|
|
4.94282 |
1.66E-11 |
16.98057 |
|
1.37E-06 |
||||||
Здесь |
|
|
|
f xk xk |
3 6xk |
2 |
3xk 11, |
||||||
2 |
|
|
|
|
f xk |
|
|
|
|
|
|
|
|
f xk 3xk |
12xk 3, xk 1 xk |
|
|
. |
|
|
|
|
|||||
f xk |
|
|
|
|
|
||||||||
В качестве |
корня можно взять |
значение: x 4,943 . Из |
|||||||||||
таблицы видно, что процесс сошелся уже на второй итерации. Для того, чтобы сравнить методы дихотомии и
касательных, |
|
найдем |
первый |
корень |
|
уравнения |
|||||||
x3 6x2 |
3x 11 0 на отрезке 2, 1 методом Ньютона: |
||||||||||||
Так |
как |
f |
|
|
|
0 на |
|
интервале |
|||||
x 6x 12 , то f |
x |
|
|||||||||||
2, 1 , а так как f 2 27 0 , то |
x0 2 . |
|
|
|
|
|
|||||||
|
|
|
|
f xk |
|
|
|
|
|
|
|||
Номер итерации |
|
xk |
f xk |
|
|
xk 1 xk |
|
|
|
||||
|
|
||||||||||||
|
|
|
|
|
|
39 |
|
|
|
|
|
|
|
0 |
|
|
|
-2 |
-27 |
|
|
- |
|
|
|
||
1 |
|
|
|
-1.30769 |
-5.41966 |
23.82249 |
|
0.692308 |
|
|
|
||
2 |
|
|
|
-1.08019 |
-0.50182 |
19.46272 |
|
0.227502 |
|
|
|
||
3 |
|
|
|
-1.05441 |
-0.00613 |
18.9882 |
|
0.025783 |
|
|
|
||
4 |
|
|
|
-1.05408 |
-9.5E-07 |
18.98229 |
|
0.000323 |
|
|
|
||
Заданная |
точность достигается |
на |
4-ой |
|
итерации. |
||||||||
Напомним, что метод дихотомии (Пример 1.2) достиг точности 0,001 лишь на 10-ой итерации.
Вычислим второй корень нашего уравнения на отрезке
1,3 . Поскольку вторая производная |
|
f x 6x 12 меняет |
18

знак на отрезке 1,3 при x 2 , уменьшим интервал изоляции
так, чтобы изменения знака не происходило. Рассмотрим |
|||||
интервал |
2,1;3 . Вычислим значения функции и второй |
||||
производной |
на |
левом |
конце |
отрезка: |
|
|
|
f 2,1 0,101 0 . |
|
|
|
f 2,1 0,6 0 , |
|
|
|||
Поскольку функция и вторая производная имеют один знак, в
качестве начального приближения выбираем x0 |
2,1. |
|
||||
Номер |
xk |
f xk |
f xk |
|
xk 1 xk |
|
|
|
|||||
итерации |
|
|
|
|
|
|
0 |
2.1 |
0.101 |
-8.97 |
- |
|
|
1 |
2.11126 |
3.95E-05 |
-8.96286 |
0.01126 |
|
|
2 |
2.111264 |
6.47E-12 |
-8.96286 |
|
4.4E-06 |
|
3 |
2.111264 |
0 |
-8.96286 |
|
7.22E-13 |
|
В сравнении с методом простой итерации значение корня было получено за две итерации вместо шести.
Эти примеры показывают, что метод Ньютона сходится быстрее, чем метод дихотомии и метод простой итерации. Но для его использования необходимо выбирать начальное приближение, достаточно близкое к корню.
Упрощенный метод Ньютона. Эта модификация метода Ньютона используется, если производная f x представляет собой сложную функцию, и для ее вычисления на каждой
итерации тратится много времени. Зададим |
x0 |
– начальное |
приближение и вычислим производную |
z |
f x0 . На |
следующих итерациях используется вычисленное значение |
|||||
производной: |
xk 1 xk |
f xk |
|
. Это упрощение несколько |
|
z |
|||||
|
|
|
|||
замедляет процесс сходимости к решению, однако сокращает время каждого итерационного цикла.
19
