В результате мы получили формулы, так называемой

квадратичной или параболической интерполяции.

ПРИМЕР 3.3. Задана таблица значений функции:

интерполяционный полином Лагранжа. Для этого случая N 3 ,

т.е. полином Лагранжа имеет третий порядок. Вычислим значения базисных полиномов при z 1 :

3

L3 z fi li z 1 0,238 0,2 1,667 0,5 1,667

i0

0,8 0,762 0,129

Итак, интерполирующая функция принимает в точке 1 значение -0,129.

Подбор эмпирических формул

При интерполировании функций мы использовали условие равенства значений интерполяционного полинома и данной функции в узлах интерполяции. Если же исходные данные получены в результате опытных измерений, полученных с некоторой погрешностью, точного выполнения условий интерполяции не требуется. В этих случаях интерполирующая

функция F(x) должна удовлетворять условиям F xi f xi , i=1, 2, …, N. Это условие означает, что интерполирующая

53

функцияF x проходит не точно через заданные точки, а в некоторой ихокрестности, как, например, показано на рис. 3.3.

y

x

Рис. 3.3. Приближенная интерполяция

Тогда говорят о подборе эмпирических формул,

описывающих заданные точки. Построение эмпирической

a0 , a1 ,..., am , и определение наилучших в некотором смысле этих

параметров. Вид формулы иногда известен из физических соображений (например, связь между напряжением и деформацией для упругой среды), или выбирается из геометрических соображений. Для этого экспериментальные точки наносятся на график и путем сравнения поведения точек с графиками известных функций подбирается общий вид зависимости. Успех в значительной степени определяется опытом и интуицией исследователя.

Для практики важен случай аппроксимации функции

многочленами, т.е. F x a0 a1 x a2 x 2 ... am x m .

После того, как выбран вид эмпирической зависимости, степень близости к эмпирическим данным определяется,

используя минимум суммы квадратов отклонений

вычисленных и экспериментальных данных.

54

Метод наименьших квадратов

неизвестными коэффициентами a0 , a1 ,..., am . Запишем сумму

квадратов отклонений между вычисленными по эмпирической формуле и заданными опытными данными:

N

S a0 , a1 ,..., am x, a0 , a1 ,..., am fi 2 .

i 1

Параметры a0 , a1 ,..., am будем находить из условия минимума функции S a0 , a1 ,..., am . В этом состоит метод

наименьших квадратов (МНК).

Известно, что в точке минимума все частные производные от S по параметрам a0 , a1 ,..., am равны нулю:

Рассмотрим применение МНК для частного случая, широко используемого на практике. В качестве эмпирической функции рассмотрим полином

x a0 a1 x a2 x 2 ... am x m .

Формула (3.2) для определения суммы квадратов отклонений примет вид:

55

Приравнивая эти выражения нулю, и собирая

Данная система уравнений называется нормальной. В результате решения этой системы линейных уравнений одним

из известных способов, находятся коэффициенты a0 , a1 ,..., am .

Как правило, выбирают несколько эмпирических зависимостей. По МНК находят коэффициенты этих зависимостей и среди них находят наилучшую по минимальной сумме отклонений.

56

Учитывая, что N 6 , и, используя Excel, находим:

6

xi2 5 2 3,5 2 2 2 1,52 3,252 52 79,0625 ,

i 1

6

fi 0,5 1,2 1,4 1,6 1,7 1,5 7,9 ,

i 1

6

fi xi 5 0,5 3,5 1,2 2 1,4 1,5 1,6 3,25 1,7 5 1,5 5,925

i 1

Решая систему линейных уравнений, получим a0 1,328 , a1 0,0875. Следовательно, линейная зависимость имеет вид:

x 1,328 0,0875x .

Вычислим сумму квадратов отклонений:

нормальных уравнений имеет вид

57

Выпишем систему нормальных уравнений для гиперболической зависимости. Согласно МНК, находим сумму квадратов отклонений:

Составляем систему нормальных уравнений:

Или

58

имеет вид x 1,299 0,5476x .

Сумма квадратов отклонений: S3 0,686 .

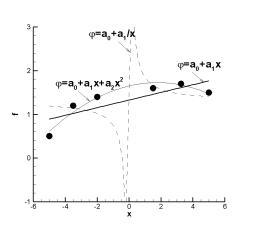
Итак, минимальным отклонением из трех рассмотренных зависимостей обладает квадратичная, т.е., она является лучшей из данных трех для аппроксимации исходных данных.

Графически результаты расчетов представлены на рис. 3.4. Маркерами отмечены исходные данные. Видно, что квадратичная зависимость действительно проходит ближе всего

к

заданн

ым

значен

иям

функци и.

Рис. 3.4. Пример выбора эмпирической зависимости

59