ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Постановка задачи
Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде
ОДУ можно записать в виде: |
|
|||
|
|
n |
0 , |
(5.1) |
F x, y, y , y ,..., y |
|
|||
где x – независимая переменная, |
y i - i -ая производная от |
|||
искомой функции, n – порядок уравнения. Общее решение ОДУ n -го порядка содержит n произвольных постоянных
c1 , c2 ,..., cn , т.е. общее решение имеет вид y x, c1 , c2 ,..., cn . Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания
дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Ясно, что при n 1 можно говорить только о задачи Коши. Примеры постановки задачи Коши:
dy x 2 y 3 |
, |
y 1 1; |
|
||||
dx |
|
|
|
|
|||
d 2 y dy |
|
2 |
y 1 1, |
|
|||
|
|
|
|
|
|
||
dx 2 dx xy , |
y 1 0 . |
||||||
Примеры краевых задач:
69
|
d 2 y |
2 |
dy |
y sin x , |
y 0 1, |
y 1 0 |
|
||||
|
dx 2 |
|
|
||||||||
|
|
dx |
|
|
|
|
|
|
|||
|
d 3 y |
|
|
|
d 2 y |
|
dy |
|
y 1 0, |
|
y 3 2 . |
|
dx3 |
x x dx 2 |
dx , |
||||||||
|
y 1 0, |
||||||||||
Решить такие |
задачи |
аналитически удается лишь для |
|||||||||
некоторых специальных типов уравнений, поэтому применение приближенных методов решения является необходимостью.
Приближенные методы решения задачи Коши для ОДУ первого порядка
Требуется найти решение y(x) ОДУ первого порядка
|
dy |
|
f x, y |
|
|
|
|
(5.2) |
||||
|
dx |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
на отрезке x0 , xn при условии |
|
|
|
|
|
|
||||||
|
y x0 y0 . |
|
|
|
|
(5.3) |
||||||
Приближенное решение будем искать в узлах расчетной |
||||||||||||
сетки |
xi x0 ih, |
i 0,1,..., n с |
|
шагом |
|
h |
xn x0 |
. |
||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
Необходимо найти |
приближенные |
значения в |
узлах сетки |
|||||||||
yi=y(xi). Результаты расчетов занесем в таблицу |
|
|
|
|
||||||||
xi |
|
x0 |
|
x1 |
|
… |
|
|
xn |
|||
|
|
|
|
|
|
|
|
|
|
|||
yi |
|
y0 |
|
y1 |
|
… |
|
|
yn |
|||
|
|
|
|
|
|
|
|
|||||
Интегрируя |
уравнение на |
отрезке xi , xi |
1 , получим |
|
|
|
|
|||||
|
|
|
|
xi 1 |
|
|
|
|
|
|
|
|
|
yi 1 |
yi f x, y dx . |
|
|
(5.4) |
|||||||
xi
Для того, чтобы найти все значения yi , нужно каким-то образом
вычислить интеграл, стоящий в правой части (5.4). Применяя различные квадратурные формулы, будем получать методы решения задачи (5.2), (5.3) разного порядка точности.
70
Метод Эйлера
Если для вычисления интеграла в (5.4) воспользоваться простейшей формулой левых прямоугольников первого порядка
xi 1 |
|
f x, y dx hf xi , yi , |
|
xi |
|
то получим явную формулу Эйлера: |
|
yi 1 yi hf xi , yi , i 0,1,..., n 1. |
(5.5) |
Явный метод Эйлера имеет первый порядок аппроксимации. Реализация метода. Поскольку x0 , y0 , f x0 , y0
известны, применяя (5.5) последовательно, определим все yi: y1 y0 hf x0 , y0 , y2 y1 hf x1 , y1 , ….
Геометрическая |
интерпретация |
метода |
Эйлера |
||
(рис. 5.1.): |
|
|
|
|
|
Пользуясь тем, что в точке x0 известно решение y x0 y0 |
|||||
и значение его производной y x0 dy |
|
|
f x0 , y0 , |
можно |
|
|
|||||
|
dx |
|
x x0 |
|
|
|
|
|
|
||
записать уравнение касательной к графику искомой функции |
|||||||
y y x |
в |
точке |
f x0 , y0 |
: |
y y0 |
f x0 , y0 x x0 . |
При |
достаточно |
малом |
шаге h |
ордината |
y1 y0 hf x0 , y0 |
этой |
||
касательной, полученная подстановкой в правую часть значения x1 x0 h , должна мало отличаться от ординаты y x1 решения
y x задачи Коши. Следовательно, точка x1 , y1 пересечения касательной с прямой x x1 может быть приближенно принята
за новую начальную точку. Через эту точку снова проведем |
|||
прямую y y1 f x1 , y1 x x1 , |
которая приближенно отражает |
||
поведение касательной к y x |
в |
точке x1 , y x1 . Подставляя |
|
сюда x2 x1 h (т.е. пересечение |
с прямой |
x x2 ), получим |
|
приближенное значение y x в точке x2 : y2 |
y1 hf x1 , y1 и |
||
т.д. В итоге для i -ой точки получим формулу Эйлера.
71
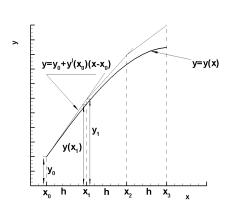
Рис. 5.1. Геометрическая интерпретация метода Эйлера
Если |
в |
(5.4) |
использовать |
формулу |
правых |
|
|
xi 1 |
|
|
|
прямоугольников: |
|
f x, y dx hf xi 1 , yi 1 , то |
получим |
||
|
|
xi |
|
|
|
неявный метод Эйлера |
|
|
|
||
|
yi 1 |
yi hf xi 1 , yi 1 , i 0,1,..., n 1. |
(5.6) |
||
Этот метод называют неявным, поскольку для вычисления |
|||||
неизвестного |
значения |
yi 1 y xi 1 по |
известному |
значению |
|
требуется решать уравнение, в общем случае
нелинейное. Неявный метод Эйлера также имеет первый порядок аппроксимации.
Модифицированный метод Эйлера
В данном методе вычисление yi 1 состоит из двух этапов:
~yi 1 yi hf xi , yi ,
|
|
h |
~ |
|
|
|
yi 1 |
yi |
|
f xi , yi f xi 1 , yi 1 |
. |
(5.7) |
|
2 |
||||||
|
|
|
|
|
Данная схема называется также методом предикторкорректор. Это английское название, означающее «предсказатьисправить». Действительно, на первом этапе приближенное значение предсказывается с первым порядком точности, а на
72