40
30
20
10
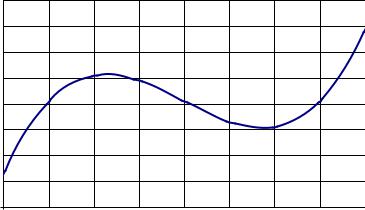
y =f (x )
0 -10 -20 -30
-40
-2 -1 0 1 2 3 4 5 6
Рис. 1.3. Иллюстрация графического способа исследования НАУ
Приближенные (итерационные) методы решения НАУ
Пусть интервалы изоляции корней известны. Познакомимся с несколькими итерационными методами, позволяющими найти корень на известном интервале изоляции [a, b].
Метод деления отрезка пополам (дихотомии).
Идея метода заключается в делении отрезка, на котором содержится корень, пополам, до тех пор, пока не будет
достигнута заданная точность. |
|
||
Поделим отрезок a,b |
|
пополам. Координата середины |
|
отрезка определится как c |
a b |
. Теперь корень остался на |
|
|
|||
одной из частей: a, c или |
2 |
Если f a f c 0 , то это |
|
c,b . |
|||
говорит о том, что функция на отрезке a, c меняет свой знак, то
есть на данном интервале находится корень. В этом случае деление отрезка можно повторить, приняв в качестве нового
10
правого конца точку c , т.е. приравняв b c . В противном случае, корень попал на половину c,b , и необходимо изменить
значение левого конца отрезка: a c . Поскольку корень всегда заключен внутри отрезка, итерационный процесс можно останавливать, если длина отрезка станет меньше заданной
точности: |
|
b a |
|
. |
|
|
|
|
|
||||
ПРИМЕР |
1.2. |
Найдем первый корень уравнения |
||||
f x x3 6x2 |
3x 11 0 с точностью 0,05 . |
|||||
Вычисления выполним при помощи электронной таблицы Excel, задавая начальные значения концов интервала изоляции и формул для выполнения итераций. Результаты оформляются в виде таблицы
|
a |
b |
c |
f(a) |
f( c) |
|b-a| |
1 |
-2 |
-1 |
-1.5 |
-27 |
-10.375 |
1 |
2 |
-1.5 |
-1 |
-1.25 |
-10.375 |
-4.078125 |
0.5 |
3 |
-1.25 |
-1 |
-1.125 -4.078125 -1.392578 |
0.25 |
||
4 |
-1.125 |
-1 |
-1.0625 |
-1.392578 |
-0.1604 |
0.125 |
5 |
-1.0625 |
-1 |
-1.03125 |
-0.1604 |
0.42868 |
0.0625 |
6 |
-1.0625 |
-1.03125 |
-1.046875 |
-0.1604 |
0.136372 |
0.03125 |
где во второй строке во втором и третьем столбцах заданы a0 ,
b0 |
– |
начальные |
границы |
интервала изоляции корня; c |
|||||||||
вычисляется по формуле c |
i |
|
ai bi |
, i 1,2,3... , а a |
, b в свою |
||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
i |
i |
|
очередь определяются как |
|
|
|
|
|
|
|||||||
|
|
|
|
0; |
|
|
|||||||
ai |
c |
i 1 |
, |
если f a |
i 1 |
f c |
i 1 |
и |
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
ai 1 , |
в противном случае |
|
|
||||||||
bbi 1 , если f ai 1 f ci 1 0;
ici 1 , в противном случае.
Врезультате расчета приближенное значение первого корня x1 1,047 при заданной величине точности 0,05 .
При 0,001 необходимо сделать большее число итераций, поэтому к приведенной выше таблице добавятся строки:
11
7 |
-1.0625 |
-1.04688 |
-1.05469 |
-0.1604 |
-0.01146 |
0.015625 |
8 |
-1.05469 |
-1.04688 |
-1.05078 |
-0.01146 |
0.062598 |
0.007813 |
9 |
-1.05469 |
-1.05078 |
-1.05273 |
-0.01146 |
0.025606 |
0.003906 |
10 |
-1.05469 |
-1.05273 |
-1.05371 |
-0.01146 |
0.007084 |
0.001953 |
11 |
-1.05469 |
-1.05371 |
-1.0542 |
-0.01146 |
-0.00218 |
0.000977 |
12 |
-1.0542 |
-1.05371 |
-1.05396 |
-0.00218 |
0.002451 |
0.000488 |
13 |
-1.0542 |
-1.05396 |
-1.05408 |
-0.00218 |
0.000134 |
0.000244 |
Как можно видеть, значение корня в этом случае x1 1,054 , что является более близким к точному значению.
Второй и третий корни находятся аналогично.
Метод простой итерации
Для метода простой итерации (МПИ) уравнение (1.1) необходимо сначала преобразовать к виду x x . Это всегда
можно сделать с помощью эквивалентных преобразований. |
||||||
Далее, выберем начальное приближение x0 a,b . Следующие |
||||||
итерации |
производятся |
по |
формуле: xk 1 xk , |
т.е. |
||
x1 x0 , |
x2 x1 , |
и |
т.д. |
Если |
последовательность |
xk , |
k 1,2,... |
сходится, то |
lim xk |
x* |
x* , то есть в пределе |
||
получаем искомое решение уравнения. Итерационный процесс следует остановить, когда xk 1 xk В качестве начального
приближения обычно берут середину отрезка a,b : x0 a 2 b .
Привести исходное уравнение (1.1) к виду x x можно бесконечным числом способов. Из всевозможных функций (x)
выбирают ту, которая порождает сходящуюся к корню последовательность xk .
Достаточное условие сходимости. Пусть x имеет производную на отрезке a,b , x a,b и x q 1 для всех x из отрезка a,b . Тогда итерационный процесс сходится
к корню уравнения, т.е. lim xk x* .
k
12
Доказательство. Из формулы МПИ следует, что xk 1 x* xk x* xk x*
Применяя теорему Лагранжа о среднем, получим
xk x* 
xk x* q xk x* .
Аналогично
xk x* q xk 1 x* , xk 1 x* q xk 2 x* и т.д.
Следовательно,
|
xk 1 x* |
|
q |
xk x* |
q 2 |
xk 1 x* |
q3 |
xk 2 x* |
|
|
||||
... qk |
|
x0 |
x* |
|
qk b a |
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||
Так как q 1, то lim qk 0 и, следовательно, lim xk |
x* . |
|||||||||||||
|
|
|
|
|
|
|
|
k |
|
k |
|
|||
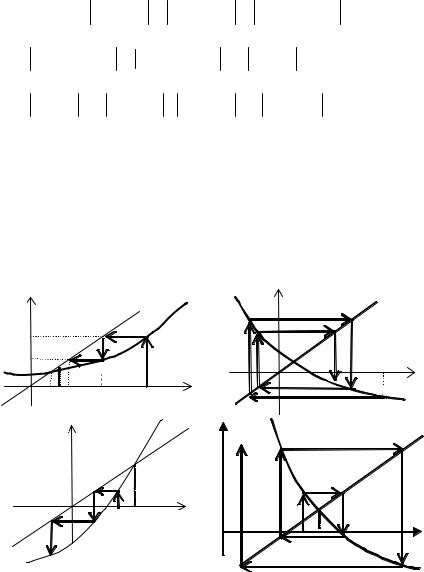
Геометрическая интерпретация метода простой итерации представлена на рис. 1.4 для случаев 0 1(а), 1 (б),
1 (в) и 1 0 (г).
y |
а |
|
y= (x) |
y |
|
б |
|
y=x |
|
|
y=x |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
y= (x) |
|
|
|
|
|
x |
x1 x3 |
x* |
x4 x2 x0 |
|
|
x* x2 |
x1 |
x0 |
|
|
x |
|
|
|
|
|
|
|||
|
в y |
y= (x) |
y г y= (x) |
|
|
||
|
|
|
y=x |
|
|
|
|
|
|
|
x |
|
|
|
y=x |
|
|
|
|
|
|
|
|
|
|
x0 |
x* |
x2 |
x* |
x1 |
x3 x |
|
|
x1 |
|
||||
|
|
|
x4 |
x0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x2 Рис. 1.4. Сходящийся (а, б) и расходящийся (в, г) МПИ
13