
- •ЛЕКЦИЯ 1
- •2. Электричество и магнетизм
- •2.1. Электростатика
- •2.1.1. Электрический заряд. Закон сохранения заряда
- •2.1.2. Взаимодействие электрических зарядов в вакууме. Закон Кулона
- •2.1.3. Электростатическое поле. Напряженность электростатического поля
- •2.1.4. Сложение электростатических полей. Принцип суперпозиции
- •2.1.5. Электростатическое поле диполя
- •2.1.6. Взаимодействие двух диполей
- •ЛЕКЦИЯ 2
- •2.1.7. Силовые линии электростатического поля
- •2.1.8. Поток вектора напряженности
- •2.1.9. Теорема Остроградского-Гаусса
- •ЛЕКЦИЯ 3
- •2.1.11. Теорема о циркуляции вектора поля
- •2.1.12. Работа сил электростатического поля. Потенциальная энергия
- •ЛЕКЦИЯ 4
- •2.1.13. Связь между напряженностью и потенциалом
- •2.1.14. Безвихревой характер электростатического поля
- •2.1.15. Силовые линии и эквипотенциальные поверхности
- •2.1.16. Расчет потенциалов простейших электростатических полей
- •ЛЕКЦИЯ 5
- •2.1.17. Поляризация диэлектриков
- •2.1.18. Различные виды диэлектриков
- •2.1.19. Вектор электрического смещения
- •ЛЕКЦИЯ 6
- •2.1.21. Изменение D и E на границе раздела двух диэлектриков
- •2.1.22. Напряженность и потенциал электростатического поля в проводнике
- •2.1.23. Определение напряженности поля вблизи поверхности заряженного проводника
- •2.1.24. Конденсаторы
- •ЛЕКЦИЯ 7
- •2.1.25. Энергия электростатического поля
- •2.1.26. Причины электрического тока
- •2.1.27. Плотность тока
- •2.1.28. Уравнение непрерывности
- •2.1.29. Сторонние силы и ЭДС
- •ЛЕКЦИЯ 8
- •2.1.30. Закон Ома для неоднородного участка цепи
- •2.1.31. Закон Ома в дифференциальной форме
- •2.1.32. Работа и мощность тока. Закон Джоуля – Ленца
- •2.1.33. КПД источника тока
- •ЛЕКЦИЯ 9
- •2.2. Электромагнетизм
- •2.2.1. Магнитные взаимодействия
- •2.2.2. 3акон Био–Савара–Лапласа
- •ЛЕКЦИЯ 10
- •2.2.3. Магнитное поле движущегося заряда
- •2.2.4. Напряженность магнитного поля
- •2.2.5. Магнитное поле прямого тока
- •2.2.6. Магнитное поле кругового тока
- •ЛЕКЦИЯ 11
- •2.2.7. Теорема Гаусса для вектора магнитной индукции
- •2.2.8. Закон Ампера
- •2.2.9. Взаимодействие двух параллельных проводников с током
- •ЛЕКЦИЯ 12
- •2.2.10. Воздействие магнитного поля на рамку с током
- •2.2.11. Сила Лоренца
- •2.2.12. Циркуляция вектора магнитной индукции
- •ЛЕКЦИЯ 13
- •2.2.13. Магнитное поле соленоида
- •2.2.14. Магнитное поле тороида
- •2.2.15. Работа по перемещению проводника с током в магнитном поле
- •ЛЕКЦИЯ 14
- •2.2.16. Опыты Фарадея. Индукционный ток. Правило Ленца
- •2.2.17. Величина ЭДС индукции
- •2.2.18. Природа ЭДС индукции
- •ЛЕКЦИЯ 15
- •2.2.19. Циркуляция вектора напряженности вихревого электрического поля
- •2.2.20. Явление самоиндукции
- •2.2.21. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
- •ЛЕКЦИЯ 16
- •2.2.22. Взаимная индукция
- •2.2.23. Индуктивность трансформатора
- •2.2.24. Энергия магнитного поля
- •2.2.25. Магнитное поле в веществе
- •ЛЕКЦИЯ 17
- •2.2.26. Диамагнетики и парамагнетики в магнитном поле
- •2.2.27. Ферромагнетики
- •2.2.28. Закон полного тока
- •ЛЕКЦИЯ 18
- •2.2.29. Ток смещения
- •2.2.30. Единая теория электрических и магнитных явлений. Система уравнений Максвелла
- •ЛЕКЦИЯ 19
- •2.3. Колебания и волны
- •2.3.1. Виды и признаки колебаний
- •2.3.2. Параметры гармонических колебаний
- •2.3.3. Графики смещения скорости и ускорения
- •2.3.4. Основное уравнение динамики гармонических колебаний
- •ЛЕКЦИЯ 20
- •2.3.5. Энергия гармонических колебаний
- •2.3.6. Математический и пружинный маятник
- •2.3.7. Гармонический осциллятор
- •2.3.8. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения
- •ЛЕКЦИЯ 21
- •2.3.9. Сложение взаимно перпендикулярных колебаний
- •2.3.10. Фигуры Лиссажу
- •2.3.11. Свободные затухающие механические колебания
- •2.3.12. Коэффициент затухания и логарифмический декремент затухания
- •ЛЕКЦИЯ 22
- •2.3.13. Вынужденные механические колебания
- •2.3.14. Свободные колебания в электрическом контуре без активного сопротивления
- •2.3.15. Свободные затухающие электрические колебания
- •ЛЕКЦИЯ 23
- •2.3.16. Вынужденные электрические колебания
- •2.3.17. Мощность, выделяемая в цепи переменного тока
- •2.3.18. Распространение волн в упругой среде
- •ЛЕКЦИЯ 24
- •2.3.19. Уравнения плоской и сферической волн
- •2.3.20. Фазовая скорость
- •2.3.21. Принцип суперпозиции. Групповая скорость
- •2.3.22. Стоячие волны
- •ЛЕКЦИЯ 25
- •2.3.23. Волновое уравнение
- •2.3.24. Дифференциальное уравнение электромагнитных волн
- •2.3.25. Энергия и импульс электромагнитного поля. Плотность потока энергии. Вектор Умова-Пойтинга
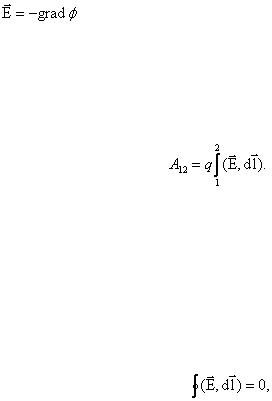
что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине.
Формула |
выражает связь потенциала с напряженностью и позволяет по |
известным значениям φ найти напряженность поля в каждой точке. Можно решить и
обратную задачу, т.е. по известным значениям E в каждой точке поля найти разность потенциаловмежду двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть, вычислена как:
С другой стороны работу можно представить в виде:
 , тогда
, тогда 
Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, ибо работа сил поля не зависит от пути. Для обхода по замкнутому контуру 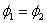 получим:
получим:
т.е. пришли к известной нам теореме о циркуляции вектора напряженности:
циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.
Поле, обладающее этим свойством, называется потенциальным.
Из обращения в нуль циркуляции вектора E следует, что линии E электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах (истоки) и на отрицательных зарядах заканчиваются (стоки) или уходят в бесконечность (рис. 2.1.30).
Это соотношение верно только для электростатического поля. Впоследствии мы с вами выясним, что поле движущихся зарядов не является потенциальным, и для него это соотношение не выполняется.
2.1.16. Расчет потенциалов простейших электростатических полей
Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами.
Разность потенциалов между точками поля, образованного двумя бесконечными заряженными плоскостями
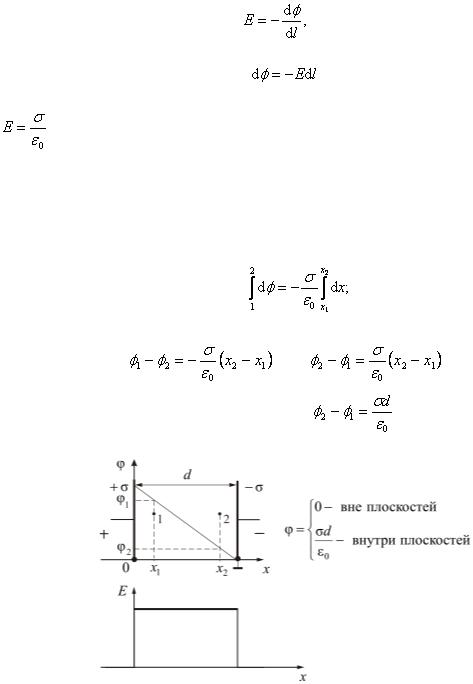
Мы показали, что напряженность связана с потенциалом
41
|
тогда |
|
|
, |
(2.1.62) |
где |
– напряженность электростатического поля между заряженными плоскостями, |
|
найденная с помощью теоремы Остроградского–Гаусса; σ = q/S– поверхностная плотность заряда.
Теперь, чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение (2.1.62):
или |
. |
(2.1.63) |
При x1 = 0 и x2 = d |
. |
(2.1.64) |
Рис. 2.1.31. Графическая зависимость напряженности E и потенциала φ от расстояния между плоскостями.
Разность потенциалов между точками поля, образованного бесконечно длинной цилиндрической поверхностью
В п. 2.1.10 с помощью теоремы Остроградского-Гаусса мы показали, что, т.к.  , то (см. рис. 2.31)
, то (см. рис. 2.31)
42
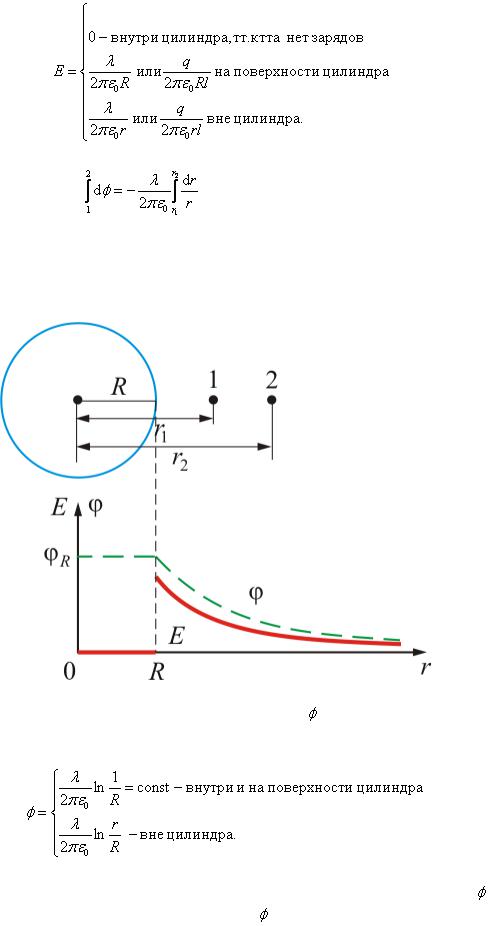
(2.1.65)
Т.к.  то , отсюда найдем разность потенциалов в произвольных точках 1 и 2:
то , отсюда найдем разность потенциалов в произвольных точках 1 и 2:
 .
.
Рис. 2.1.32. Зависимость напряженности E и потенциала |
от r для бесконечно длинной |
цилиндрической поверхности |
|
(2.1.66)
На рисунке 2.1.32 изображена зависимость напряженности E и потенциала |
от r. |
(Здесь и далее E – изображена сплошной линией, а – пунктирной). |
|
Разность потенциалов между обкладками цилиндрического конденсатора
43
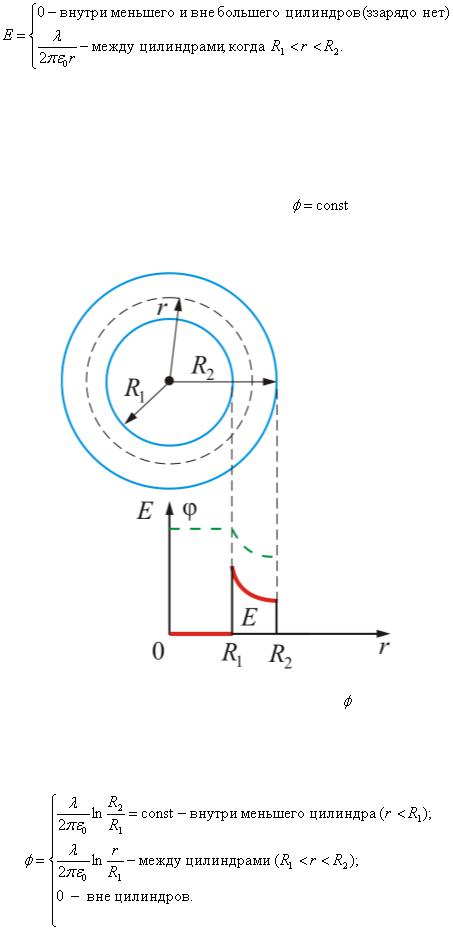
В п. 2.1.10. мы нашли, что (рис. 2.1.33)
Отсюда так же, как и в предыдущем случае, разность потенциалов будет равна:
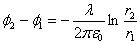 .
.
Таким образом, внутри меньшего цилиндра имеем , Е = 0, между обкладками
потенциал уменьшается по логарифмическому закону, а вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и Е равны нулю.
Рис. 2.1.33. Зависимость напряженности E и потенциала |
от r между обкладками |
цилиндрического конденсатора |
|
(2.1.67)
44
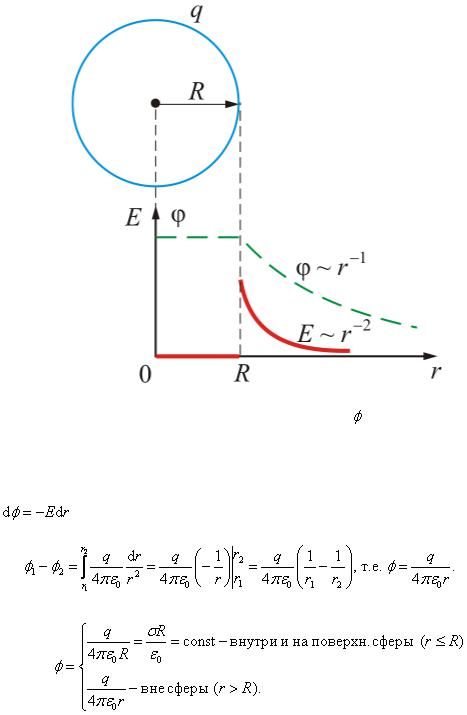
Разность потенциалов между точками поля, образованного заряженной сферой (пустотелой)
Напряженность поля сферы (рис. 2.1.34) определяется формулой:  .
.
Рис. 2.1.34 Зависимость напряженности E и потенциала |
от r заряженной пустотелой |
|
сферой |
|
|
Т.к. |
, то |
|
(2.1.68)
Разность потенциалов внутри диэлектрического заряженного шара
Имеем диэлектрический шар (рис. 2.1.35), заряженный с объемной плотностью
45

В п. 2.1.10 с помощью теоремы Остроградского–Гаусса мы нашли, что внутри шара
 .
.
Рис. 2.1.35. Зависимость напряженности E и потенциала |
от r диэлектрического |
заряженного шара |
|
Теперь найдем разность потенциалов внутри шара: |
|
или
46
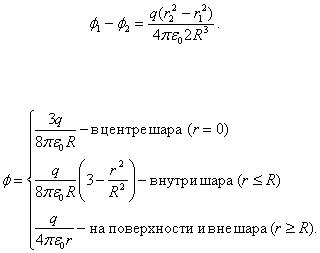
Отсюда находим потенциал шара:
(2.1.69)
Из полученных соотношений можно сделать следующие выводы.
С помощью теоремы Гаусса сравнительно просто можно рассчитать Е и φ от различных заряженных поверхностей.
Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.
Потенциал поля – всегда непрерывная функция координат.
47
