ЛЕКЦИЯ 22
2.3.13. Вынужденные механические колебания
Рассмотрим систему, на которую, кроме упругой силы (– kx) и сил сопротивления (– rυ), действует добавочная периодическая сила F – вынуждающая сила. Для колебаний вдоль оси x запишем:
– основное уравнение колебательного процесса, или
(2.3.37)
,
где fx = Fx/m – вынуждающая сила, изменяющаяся по гармоническому закону:
Через некоторое время после начала действия вынуждающей силы колебания системы будут совершаться с частотой вынуждающей силы ω.
Уравнение установившихся вынужденных колебаний:
. (2.3.38)
Наша задача найти амплитуду А и разность фаз φ между смещением вынужденных колебаний и вынуждающей силой.
Обратим внимание на то, что скорость на π/2 опережает смещение, а ускорение на π/2 опережает скорость.
Из (2.3.38) получим:
(2.3.39)
,
(2.3.40)
.
Преобразуем и (2.3.38) через косинус:
. (2.3.41)
Обозначим 
– угол между смещением и вынуждающей силой.
Подставим (2.3.39), (2.3.40) и (2.3.41) в (2.3.37):
169
Каждое слагаемое последнего уравнения можно представить в виде соответствующего вращающегося вектора амплитуды:
– амплитуда ускорения; 
– амплитуда скорости; 
– амплитуда смещения; 
– амплитуда вынуждающей силы, причем 
Вектор амплитуды силы найдем по правилу сложения векторов:
.
Рис. 2.3.16. Векторная диаграмма
Из рис. 2.3.16. видно, что 
. Найдем амплитуду А:
(2.3.42)
.
Таким образом,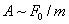 
и 
.
При постоянных F0, m и β амплитуда зависит только от соотношения круговых частот вынуждающей силы ω и свободных незатухающих колебаний системы ω0.
Начальную фазу вынужденных колебаний можно найти из выражения
170
(2.3.43)
Из рис. 2.3.16. видно, что сила опережает смещение на угол, который определяется из выражения
.
Проанализируем выражение (2.3.42).
1) 
(частота вынуждающей силы равна нулю), тогда
– статическая амплитуда (колебания не совершаются).
2) 
(затухания нет). С увеличением ω (но при 
) амплитуда растет и при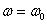 
резко возрастает ( 
). Это явление называется резонанс. При дальнейшем увеличении ω ( 
) амплитуда опять уменьшается (рис. 2.3.17).
Рис. 2.3.17
3) 
Амплитуда будет максимальна при минимальном значении знаменателя.
Для нахождения точки перегиба возьмем первую производную по ω от подкоренного выражения (2.3.42) и приравняем ее к нулю:
4ω ≠ 0, следовательно, выражение в скобках равно нулю:
, отсюда
171
, |
(2.3.44) |
|
где ωрез – резонансная частота.
Явление возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к ωрез называется резонансом.
Для консервативной системы, т.е. 
из (2.3.44) следует 
с; для диссипативной ωрез несколько меньше собственной круговой частоты ω0 (рис. 2.3.17).
С увеличением коэффициента затухания β явление резонанса проявляется все слабее и исчезает при 
.
2.3.14. Свободные колебания в электрическом контуре без активного сопротивления
В цепи, содержащей индуктивность L и ёмкость С, могут возникать электрические колебания. Такая цепь называется колебательным контуром (рис. 2.3.18).
Рис. 2.3.18. Колебательный контур
Колебания в контуре можно вызвать либо зарядив конденсатор, либо вызвав в индуктивности ток (например включив магнитное поле).
Поскольку активное сопротивление контура , полная энергия остаётся постоянной. Если энергия конденсатора равна нулю, то энергия магнитного поля максимальна, и наоборот. Рассмотрим процессы, происходящие в колебательном контуре, в сравнении с колебаниями маятника (рис. 2.3.19).
172
Рис. 2.3.19. Сравнение процессов, происходящих в колебательном контуре, в сравнении с колебаниями маятника
Из сопоставления электрических и механических колебаний (рис. 2.3.19) следует, что энергия электрического поля 
аналогична потенциальной энергии mgh или
1/2kx2, а энергия магнитного поля |
аналогична кинетической энергии |
; L |
играет роль массы т, 1/С – роль коэффициента жесткости k. Наконец, заряду q соответствует смещение маятника из положения равновесия х, силе тока I – скорость υ, а напряжению U – ускорение а.
Ниже мы увидим, что эта аналогия сохраняется и в математических уравнениях. В соответствии со вторым законом Кирхгофа (и законом сохранения энергии), можно записать:
(2.3.45)
.
Но, т.к. |
тогда получим |
. |
Введем обозначение: 
– собственная частота контура, отсюда получим
основное уравнение колебаний в контуре:
173