; (2mp = const).
Так как 
– фазовая скорость, то 
– групповая скорость. С такой
скоростью перемещается максимум амплитуды. В пределе выражение для групповой скорости:
(2.3.81)
.
Это выражение справедливо для центра группы произвольного числа волн. Выражению для групповой скорости можно придать другой вид. Т.к , следовательно
.
Выразим 
через длину волны l:
; 
; 
,
, тогда получим
|
|
. |
(2.3.82) |
|
|
|
|
|
|
Из этой формулы следует, |
что в диспергирующей среде, в зависимости от знака |
, |
||
групповая скорость может быть больше или меньше фазовой. |
|
|
||
В отсутствие дисперсии |
и |
. Максимум интенсивности приходится на |
||
центр группы волн. Поэтому скорость переноса энергии равна групповой скорости.
Понятие групповой скорости применимо только при условии, что поглощение энергии волны в среде невелико. При значительном затухании волн понятие групповой скорости утрачивает смысл. Это случай из области аномальной дисперсии (рассмотрим позже).
2.3.22. Стоячие волны
Если в среде распространяется несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Волны накладываются друг на друга, не возмущая (не искажая друг друга). Это и есть принцип суперпозиции волн.
191
Если две волны, приходящие в какую-либо точку пространства, обладают постоянной разностью фаз, такие волны называются когерентными. При сложении когерентных волн возникает явление интерференции.
Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении от преград.
Напишем уравнения двух плоских волн, распространяющихся в противоположных направлениях (начальная фаза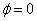 
):
(2.3.83)
.
Сложим уравнения и преобразуем по формуле суммы косинусов (2.3.79):
.
Т.к. 
, то можно записать:
.
Учитывая, что 
, получим уравнение стоячей волны:
(2.3.84)
.
В выражении для фазы не входит координата, поэтому можно записать:
, |
(2.3.85) |
где суммарная амплитуда 
.
В точках, где координаты удовлетворяют условию |
(n = 1, 2, 3, …), |
, суммарная амплитуда равна максимальному значению: 
, – это
пучности стоячей волны. Координаты пучностей:
. (2.3.86)
192
а |
Б |
Рис. 2.3.32. Образование стоячих волн
В точках, координаты которых удовлетворяют условию 
(n = 0, 1,
2,…), 
и суммарная амплитуда колебаний равна нулю 
, – это узлы
стоячей волны. Координаты узлов:
(2.3.87)
.
Точки среды, находящиеся в узлах, колебаний не совершают.
Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (рис. 5.5, а), и узел – если более плотная
(рис. 2.3.32, б).
Если рассматривать бегущую волну, то в направлении ее распространения
переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.
193