ЛЕКЦИЯ 3
2.1.10. Вычисление электрических полей с помощью теоремы Остроградского
– Гаусса
Продемонстрируем возможности теоремы Остроградского-Гаусса на нескольких примерах.
Поле бесконечной однородно заряженной плоскости
Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:
где dq – заряд, сосредоточенный на площади dS; dS – физически бесконечно малый участок поверхности.
Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный.
Напряженность 
во всех точках будет иметь направление, перпендикулярное плоскости
S (рис. 2.1.20).
Очевидно, что в симметричных, относительно плоскости точках, напряженность 
будет одинакова по величине и противоположна по направлению.
Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями S, расположенными симметрично относительно плоскости (рис. 2.1.21).
Рис. 2.1.20 Рис. 2.1.21
Тогда 
Применим теорему Остроградского-Гаусса. Поток ФЕ через боковую часть поверхности цилиндра равен нулю, т.к.
Для основания цилиндра 
Суммарный поток через замкнутую поверхность (цилиндр) будет равен:
26
Внутри поверхности заключен заряд q =σ∆S . Следовательно, из теоремы Остроградского–Гаусса получим:
;
откуда видно, что напряженность поля плоскости S равна:
(2.1.32)
Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости 
Поле двух равномерно заряженных плоскостей
Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ (рис. 2.1.22).
Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей 
.
Тогда внутри плоскостей
(2.1.33)
Вне плоскостей напряженность поля 
Рис. 2.1.22. Поле двух заряженных плоскостей
Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).
Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):
27
, т.е.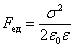 
. (2.1.34)
Механические силы, действующие между заряженными телами, называют
пондермоторными.
Тогда сила притяжения между пластинами конденсатора:
(2.1.35)
где S – площадь обкладок конденсатора. Т.к. 
, то
. (2.1.36)
Это формула для расчета пондермоторной силы.
Поле заряженного бесконечно длинного цилиндра (нити)
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R,
заряженной с постоянной линейной плотностью |
, где dq – заряд, |
сосредоточенный на отрезке цилиндра (рис. 2.1.23). |
|
Рис. 2.1.23 Бесконечно длинный цилиндр (нить)
Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.
Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для
оснований цилиндров 
для боковой поверхности 
т.е. зависит от расстояния r.
28
Следовательно, поток вектора |
через рассматриваемую поверхность, равен |
При 
на поверхности будет заряд 
По теореме Остроградского-Гаусса
, отсюда
(2.1.37)
.
Если 
, т.к. внутри замкнутой поверхности зарядов нет (рис.2.1.24).
Рис. 2.1.24. Поле бесконечно длинного цилиндра (нити)
Если уменьшать радиус цилиндра R (при |
), то можно вблизи поверхности |
получить поле с очень большой напряженностью и, при |
, получить нить. |
Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком
Внутри меньшего и вне большего цилиндров поле будет отсутствовать 
(рис.
2.1.25).
29
Рис. 2.1.25. Поле двух коаксиальных цилиндров
В зазоре между цилиндрами, поле определяется так же, как и в предыдущем случае:
Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор).
Поле заряженного пустотелого шара
Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным, 
– в любой точке проходит через центр шара. |
,и силовые линии перпендикулярны |
|
поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.1.26). |
||
Если |
то внутрь воображаемой сферы попадет весь заряд q, распределенный по |
|
сфере, тогда
,
откуда поле вне сферы:
(2.1.38)
Внутри сферы, при 
поле будет равно нулю, т.к. там нет зарядов: 
30
Рис. 2.1.26. Поле заряженного пустотелого шара
Как видно из (2.1.38) вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.
Поле объемного заряженного шара
Для поля вне шара радиусом R (рис. 2.1.27) получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула:
.
Но внутри шара при |
сферическая поверхность будет содержать в себе заряд, |
равный |
|
где ρ – объемная плотность заряда, равная: 
; 
– объем шара. Тогда по теореме Остроградского-Гаусса запишем:
,
т.е. внутри шара
. (2.1.39)
Таким образом, внутри шара 
31