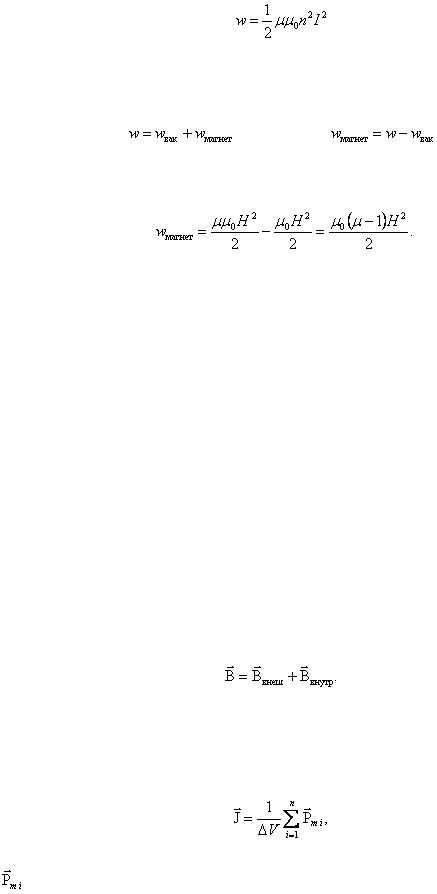
(2.2.75)
,
Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника:
, отсюда |
. |
|
Т.к. в вакууме 
, имеем
2.2.25. Магнитное поле в веществе
При изучении магнитного поля в веществе различают два типа токов – макротоки и
микротоки.
Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел.
Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах.
Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего, или собственного, магнитного поля, создаваемого микротоками.
Характеризует магнитное поле в веществе вектор B , равный геометрической сумм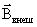е 
и 
магнитных полей:
, |
(2.2.76) |
|
Количественной характеристикой намагниченного состояния вещества служит
векторная величина – намагниченность J , равная отношению магнитного момента малого объема вещества к величине этого объема:
|
(2.2.77) |
|
, |
где |
– магнитный момент i-го атома из числа n атомов, в объеме V. |
|
Для того чтобы связать вектор намагниченности среды J с током I микро , рассмотрим |
равномерно намагниченный параллельно оси цилиндрический стержень длиной h и
130
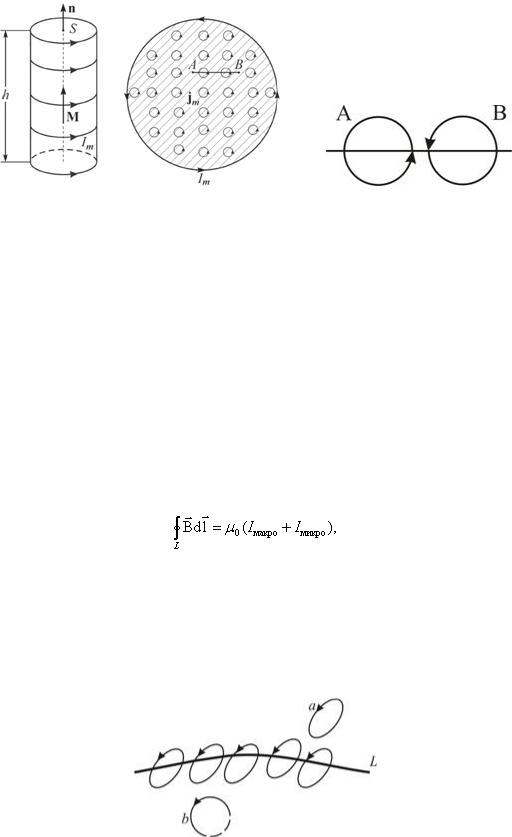
поперечным сечением S (рис. 2.2.41, а). Равномерная намагниченность означает, что плотность атомных циркулирующих токов внутри материала I микро повсюду постоянна.
а |
б |
в |
Рис. 2.2.41
Каждый атомный ток в плоскости сечения стержня, перпендикулярной его оси, представляет микроскопический кружок, причем все микротоки текут в одном направлении – против часовой стрелки (рис. 2.2.41), б). В местах соприкосновения отдельных атомов и молекул (А, В) молекулярные токи противоположно направлены и компенсируют друг друга (рис. 2.2.41, в). Нескомпенсированными остаются лишь токи, текущие вблизи поверхности материала, создавая на поверхности материала некоторый
микроток I микро , возбуждающий во внешнем пространстве магнитное поле, равное полю, созданному всеми молекулярными токами.
Закон полного тока для магнитного поля в вакууме можно обобщить на случай магнитного поля в веществе:
|
|
(2.2.78) |
где I микро и I макро – алгебраическая сумма |
макро- и микротоков |
сквозь поверхность, |
натянутую на замкнутый контур L. |
|
|
Как видно из рисунка 2.2.42, вклад в |
I микро дают только те |
молекулярные токи, |
которые нанизаны на замкнутый контур L. |
|
|
Рис. 6.4
131
Алгебраическая сумма сил микротоков связана с циркуляцией вектора намагниченности соотношением
(2.2.79)
,
тогда закон полного тока можно записать в виде
(2.2.80)
,
Вектор
называется напряженностью магнитного поля.
|
Таким образом, закон полного тока для магнитного поля в веществе утверждает, что |
|
циркуляция вектора напряженности магнитного поля |
H вдоль произвольного |
|
замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность, |
||
натянутую на этот контур: |
|
|
|
, |
(2.2.81) |
|
|
|
|
Выражение (2.2.81)– это закон полного тока в интегральной форме. В |
|
дифференциальной форме его можно записать: |
|
|
|
, |
(2.2.82) |
|
|
|
|
Намагниченность изотропной среды с напряженностью H связаны соотношением: |
|
|
, |
(2.2.83) |
где |
– коэффициент пропорциональности, характеризующий магнитные свойства |
|
вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением 
.
132