
- •ЛЕКЦИЯ 1
- •2. Электричество и магнетизм
- •2.1. Электростатика
- •2.1.1. Электрический заряд. Закон сохранения заряда
- •2.1.2. Взаимодействие электрических зарядов в вакууме. Закон Кулона
- •2.1.3. Электростатическое поле. Напряженность электростатического поля
- •2.1.4. Сложение электростатических полей. Принцип суперпозиции
- •2.1.5. Электростатическое поле диполя
- •2.1.6. Взаимодействие двух диполей
- •ЛЕКЦИЯ 2
- •2.1.7. Силовые линии электростатического поля
- •2.1.8. Поток вектора напряженности
- •2.1.9. Теорема Остроградского-Гаусса
- •ЛЕКЦИЯ 3
- •2.1.11. Теорема о циркуляции вектора поля
- •2.1.12. Работа сил электростатического поля. Потенциальная энергия
- •ЛЕКЦИЯ 4
- •2.1.13. Связь между напряженностью и потенциалом
- •2.1.14. Безвихревой характер электростатического поля
- •2.1.15. Силовые линии и эквипотенциальные поверхности
- •2.1.16. Расчет потенциалов простейших электростатических полей
- •ЛЕКЦИЯ 5
- •2.1.17. Поляризация диэлектриков
- •2.1.18. Различные виды диэлектриков
- •2.1.19. Вектор электрического смещения
- •ЛЕКЦИЯ 6
- •2.1.21. Изменение D и E на границе раздела двух диэлектриков
- •2.1.22. Напряженность и потенциал электростатического поля в проводнике
- •2.1.23. Определение напряженности поля вблизи поверхности заряженного проводника
- •2.1.24. Конденсаторы
- •ЛЕКЦИЯ 7
- •2.1.25. Энергия электростатического поля
- •2.1.26. Причины электрического тока
- •2.1.27. Плотность тока
- •2.1.28. Уравнение непрерывности
- •2.1.29. Сторонние силы и ЭДС
- •ЛЕКЦИЯ 8
- •2.1.30. Закон Ома для неоднородного участка цепи
- •2.1.31. Закон Ома в дифференциальной форме
- •2.1.32. Работа и мощность тока. Закон Джоуля – Ленца
- •2.1.33. КПД источника тока
- •ЛЕКЦИЯ 9
- •2.2. Электромагнетизм
- •2.2.1. Магнитные взаимодействия
- •2.2.2. 3акон Био–Савара–Лапласа
- •ЛЕКЦИЯ 10
- •2.2.3. Магнитное поле движущегося заряда
- •2.2.4. Напряженность магнитного поля
- •2.2.5. Магнитное поле прямого тока
- •2.2.6. Магнитное поле кругового тока
- •ЛЕКЦИЯ 11
- •2.2.7. Теорема Гаусса для вектора магнитной индукции
- •2.2.8. Закон Ампера
- •2.2.9. Взаимодействие двух параллельных проводников с током
- •ЛЕКЦИЯ 12
- •2.2.10. Воздействие магнитного поля на рамку с током
- •2.2.11. Сила Лоренца
- •2.2.12. Циркуляция вектора магнитной индукции
- •ЛЕКЦИЯ 13
- •2.2.13. Магнитное поле соленоида
- •2.2.14. Магнитное поле тороида
- •2.2.15. Работа по перемещению проводника с током в магнитном поле
- •ЛЕКЦИЯ 14
- •2.2.16. Опыты Фарадея. Индукционный ток. Правило Ленца
- •2.2.17. Величина ЭДС индукции
- •2.2.18. Природа ЭДС индукции
- •ЛЕКЦИЯ 15
- •2.2.19. Циркуляция вектора напряженности вихревого электрического поля
- •2.2.20. Явление самоиндукции
- •2.2.21. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
- •ЛЕКЦИЯ 16
- •2.2.22. Взаимная индукция
- •2.2.23. Индуктивность трансформатора
- •2.2.24. Энергия магнитного поля
- •2.2.25. Магнитное поле в веществе
- •ЛЕКЦИЯ 17
- •2.2.26. Диамагнетики и парамагнетики в магнитном поле
- •2.2.27. Ферромагнетики
- •2.2.28. Закон полного тока
- •ЛЕКЦИЯ 18
- •2.2.29. Ток смещения
- •2.2.30. Единая теория электрических и магнитных явлений. Система уравнений Максвелла
- •ЛЕКЦИЯ 19
- •2.3. Колебания и волны
- •2.3.1. Виды и признаки колебаний
- •2.3.2. Параметры гармонических колебаний
- •2.3.3. Графики смещения скорости и ускорения
- •2.3.4. Основное уравнение динамики гармонических колебаний
- •ЛЕКЦИЯ 20
- •2.3.5. Энергия гармонических колебаний
- •2.3.6. Математический и пружинный маятник
- •2.3.7. Гармонический осциллятор
- •2.3.8. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения
- •ЛЕКЦИЯ 21
- •2.3.9. Сложение взаимно перпендикулярных колебаний
- •2.3.10. Фигуры Лиссажу
- •2.3.11. Свободные затухающие механические колебания
- •2.3.12. Коэффициент затухания и логарифмический декремент затухания
- •ЛЕКЦИЯ 22
- •2.3.13. Вынужденные механические колебания
- •2.3.14. Свободные колебания в электрическом контуре без активного сопротивления
- •2.3.15. Свободные затухающие электрические колебания
- •ЛЕКЦИЯ 23
- •2.3.16. Вынужденные электрические колебания
- •2.3.17. Мощность, выделяемая в цепи переменного тока
- •2.3.18. Распространение волн в упругой среде
- •ЛЕКЦИЯ 24
- •2.3.19. Уравнения плоской и сферической волн
- •2.3.20. Фазовая скорость
- •2.3.21. Принцип суперпозиции. Групповая скорость
- •2.3.22. Стоячие волны
- •ЛЕКЦИЯ 25
- •2.3.23. Волновое уравнение
- •2.3.24. Дифференциальное уравнение электромагнитных волн
- •2.3.25. Энергия и импульс электромагнитного поля. Плотность потока энергии. Вектор Умова-Пойтинга
ЛЕКЦИЯ 16
2.2.22. Взаимная индукция
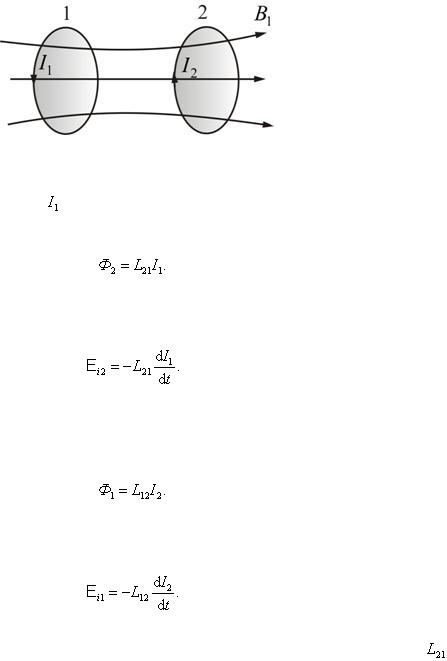
Возьмем два контура, расположенные недалеко друг от друга, как это показано на рисунке
2.2.38
Рис. 2.2.38
В первом контуре течет ток . Он создает магнитный поток, который пронизывает и витки второго контура.
, |
(2.2.63) |
При изменении тока  во втором контуре наводится ЭДС индукции:
во втором контуре наводится ЭДС индукции:
(2.2.64)
,
Аналогично, ток  второго контура создает магнитный поток, пронизывающий первый контур:
второго контура создает магнитный поток, пронизывающий первый контур:
, |
(2.2.65) |
И при изменении тока  наводится ЭДС:
наводится ЭДС:
(2.2.66)
,
Контуры называются связанными, а явление – взаимной индукцией. Коэффициенты и  называются взаимной индуктивностью, или коэффициентами взаимной индукции.
называются взаимной индуктивностью, или коэффициентами взаимной индукции.
Причём 
Трансформатор является типичным примером двух связанных контуров. Рассмотрим индуктивность трансформатора и найдем коэффициент трансформации.
126
2.2.23. Индуктивность трансформатора
Итак, явление взаимной индукции используется в широко распространенных устройствах
– трансформаторах.
Трансформатор был изобретен Яблочковым, русским ученым, в 1876 г. для раздельного питания отдельных электрических источников света (свечи Яблочкова).
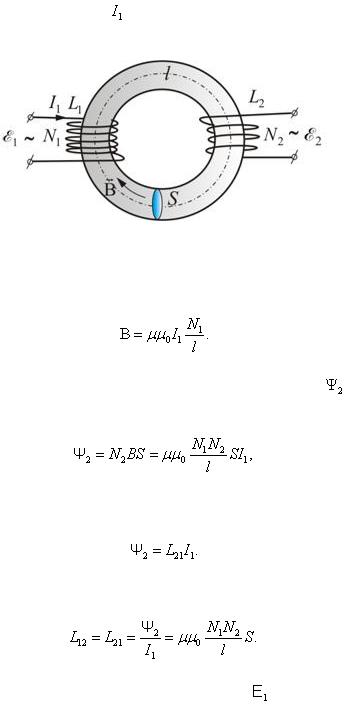
Рассчитаем взаимную индуктивность двух катушек  и
и  , намотанных на общий сердечник (рис. 2.2.39).
, намотанных на общий сердечник (рис. 2.2.39).
Когда в первой катушке идет ток , в сердечнике возникает магнитная индукция B и магнитный поток Ф через поперечное сечение S.
Рис. 2.2.39
Магнитное поле тороида можно рассчитать по формуле
Через вторую обмотку проходит полный магнитный поток |
, сцепленный со |
второй обмоткой: |
|
здесь  – потокосцепление, которое можно найти по формуле:
– потокосцепление, которое можно найти по формуле:
По определению, взаимная индуктивность двух катушек равна:
К первичной обмотке подключена переменная ЭДС . По закону Ома ток в этой цепи будет определяться алгебраической суммой внешней ЭДС и ЭДС индукции.
127
где  – сопротивление обмотки.
– сопротивление обмотки.
 – делают малым (медные провода) и
– делают малым (медные провода) и  . Тогда
. Тогда
Во второй обмотке, по аналогии,  , отсюда
, отсюда
 ,
,
Если пренебречь потерями, т.е. предположить, что  , то
, то
,
Коэффициент трансформации будет равен:
2.2.24. Энергия магнитного поля
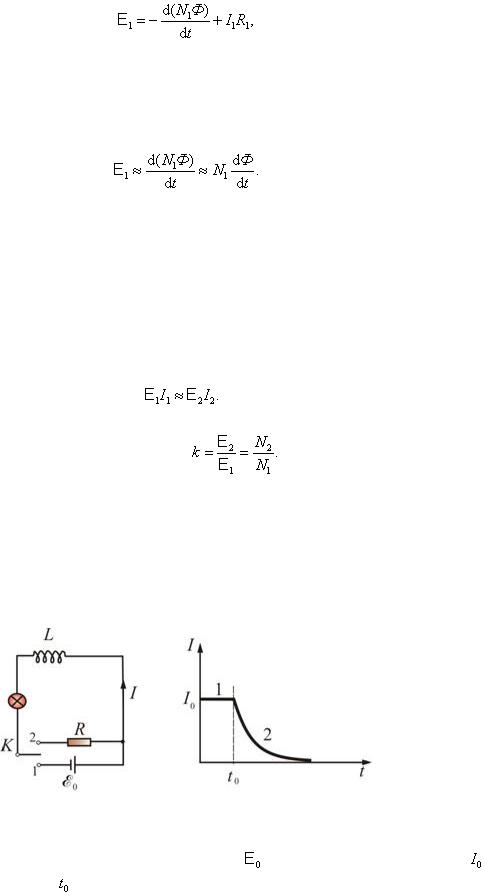
Рассмотрим случай, о котором мы уже говорили (рис. 2.2.40).
Рис. 2.2.40
(2.2.67)
(2.2.68)
Сначала замкнем соленоид L на источник ЭДС |
, в нем будет протекать ток |
. |
|
Затем в момент времени |
переключим ключ в положение 2 – замкнем соленоид на |
||
сопротивление R. В цепи будет течь убывающий ток I. При этом будет совершена работа:  , или
, или
128

(2.2.69)
,
Эта работа пойдет на нагревание проводников. Но откуда взялась эта энергия? Поскольку других изменений, кроме исчезновения магнитного поля в окружном пространстве, не произошло, остается заключить, что энергия была локализована в магнитном поле. Значит, проводник с индуктивностью L, по которой течет ток I, обладает энергией
(2.2.70)
,
Выразим энергию магнитного поля через параметры магнитного поля. Для соленоида:
 .
.
 ; отсюда
; отсюда 
Подставим эти значения в формулу (2.2.70):
(2.2.71)
,
Обозначим w – плотность энергии, или энергия в объеме V, тогда
(2.2.72)
,
но т.к.  , то
, то
(2.2.73)
или
Энергия однородного магнитного поля в длинном соленоиде может быть рассчитана по формуле
(2.2.74)
,
а плотность энергии
129
