Тема 9. Выборочное наблюдение

Под выборочным наблюдением понимается такое несплошное наблюдение, при котором статистическому наблюдению подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу – по обследуемой части дать характеристику всей совокупности единиц. Совокупность отобранных для обследования единиц называют выборочной, а совокупность единиц, из которых производится отбор, - генеральной.

Выборка может быть повторной и бесповторной.

Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу, без каких-либо элементов системности.

Типическая выборка применяется в случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп.

Выборка характеризуется следующими показателями:

- предельная ошибка выборки, она дает возможность выяснить, в каких пределах находится величина генеральной средней;

- средняя ошибка выборки, она зависит также и от способа отбора выборки.

- предельная ошибка выборочной доли;

- средняя ошибка выборочной доли.

Средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Однако о величине этой ошибки можно судить с определенной вероятностью. На величину вероятности указывает множитель . Обычно используются нормированные значения, для определенных значений вероятности.

Зная выборочную среднюю величину признака и предельную ошибку выборкиможно определить границы (пределы), в которых заключена генеральная средняя:

.

Зная выборочную долю признака и предельную ошибку выборкиможно определить границы (пределы), в которых заключена генеральная доля:

.

Предельная ошибка рассчитывается по-разному в зависимости от способа проведения отбора при проведении выборки:

	Повторный		Бесповторный
	Для средней	Для доли	Для средней	Для доли
Собственно-случайная выборка
Типическая выборка

Для определения необходимой численности выборки необходимо задать уровень точности выборочной совокупности с определенной вероятностью. Необходимый объем выборки определяется по следующей формулам:

	Повторный		Бесповторный
	Для средней	Для доли	Для средней	Для доли
Собственно-случайная выборка
Типическая выборка

Решение типовых задач.

№ 1. Из партии электроламп взята 20%-ная случайная бесповторная выборка для определения среднего веса спирали. Результаты выборки следующие:

Вес, мг	38-40	40-42	42-44	44-46
Число спиралей	15	30	45	10

Определить с вероятностью 0,954 доверительные пределы, в которых лежит средний вес спирали, для всей партии электроламп.

Решение:

мг

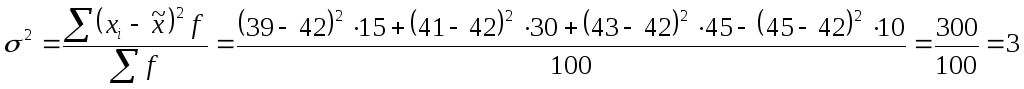
При вероятности P=0,954 t=2.

,

Доверительные интервалы для генеральной средней с вероятностью Р=0,95:

41,69 мг.42,31 мг.

№2. На заводе электроламп из партии продукции в количестве 16000 шт. ламп взято на выборку 1600 шт. (случайный, бесповторный отбор), из которых 40 шт. оказались бракованными. Определить с вероятностью 0,997 пределы, в которых будет находиться процент брака для всей партии продукции.

Решение:

Определяется доля бракованной продукции по выборке:

или 2,5%

При вероятности Р = 0,997 t = 3

Размер предельной ошибки:

или 1,11%

Доверительные интервалы для генеральной доли с вероятностью Р = 0,997:

2,5-1,11 2,5+1,11;

1,39%3,61%.

№3. 10% - бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам:

Цех	Всего рабочих, чел.	Обследовано, чел.	Число дней временной нетрудоспособности за год
			средняя	дисперсия
I	1000	100	18	49
II	1400	140	12	25
III	800	80	15	16

Определите с вероятностью 0,954 среднее число временной нетрудоспособности для всего предприятия.

,

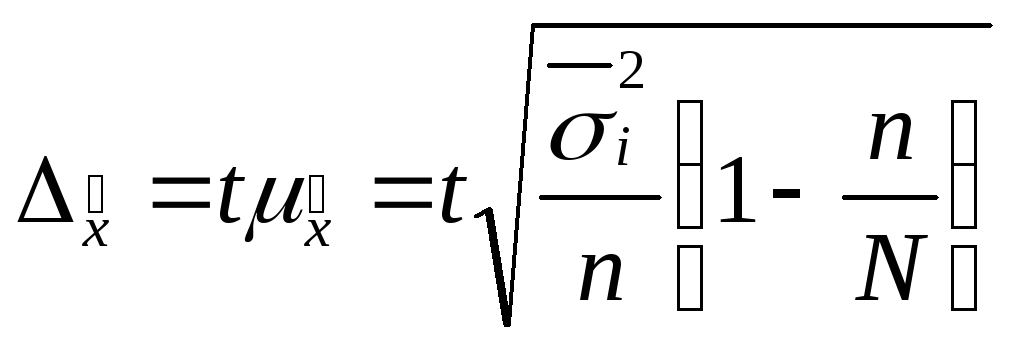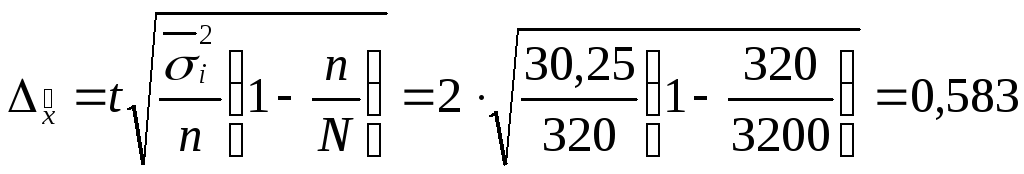
дня

14,017 дней15,183 дней.

№4. По данным пробного обследования среднее квадратическое отклонение веса нарезных батонов составило 15,4 г. Необходимо установить оптимальный объем выборки из партии нарезных батонов (2000 шт.), чтобы с вероятностью 0,997 предельная ошибка выборки не превысила 3% веса 500-граммового батона.

Решение:

σ = 15,4 г.

= 3%

N = 2000 шт.

= 500 г.

Заданную относительную ошибку выборки выразим абсолютной величиной:

г.

Значение коэффициента доверия, соответствующее вероятности 0,997, t=3

Подставляем значения в формулу для бесповторного отбора:

шт.

Итак, для соблюдения указанных условий требуется провести обследование 10 батонов.

№5. В фермерских хозяйствах области 10000 коров. Из них в районе А – 5000, в районе Б – 3000, в районе В – 2000. С целью определения средней удойности предполагается провести типическую выборку коров. Какое количество коров следует отобрать, чтобы с вероятностью 0,954 ошибка выборки не превышала 5 л., если на основе предыдущих обследований известно, что дисперсия типической выборки равна 1600?

Решение:

коров

коров, коров,коров.