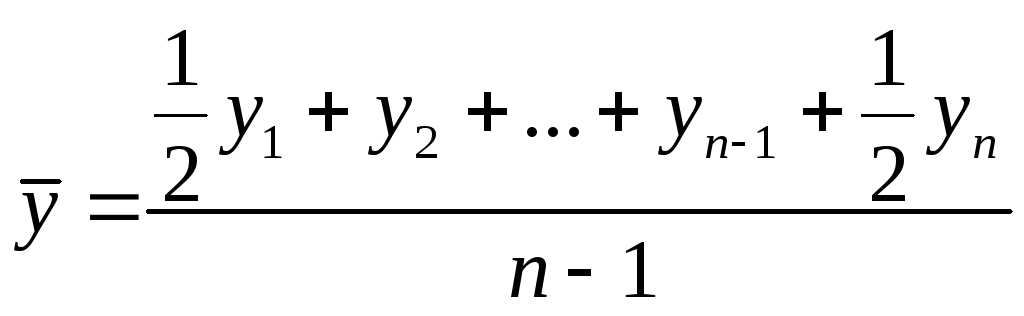Средние показатели динамики.

Метод расчета средних показателей динамики:

Наименование показателя	Метод расчета
1. Средний уровень ряда : а) для интервального ряда
б) для моментного ряда с равными интервалами
в) для моментного ряда с неравными интервалами
2. Средний абсолютный прирост,
3. Средний коэффициент роста,
4. Средний темп роста , %
5. Средний темп прироста , %
6. Средняя величина абсолютного значения 1 % прироста

При написании формул приняты следующие условные обозначения: - все уровни последовательных периодов (дат),n - число уровней ряда, t - продолжительность периода, в течение которого уровень не изменялся.

Статистические методы выявления трендов.

Временной ряд называют стационарным, если в нем отсутствует тенденция развития. Это значит, что уровни ряда варьируют вокруг среднего уровня, отклонения от которого представляют собой случайную колеблемость. Такие ряды в экономике сравнительно редки, чаще наблюдаются ряды с тенденцией.

Для того чтобы определить является ли временной ряд стационарным или нет, его разбивают на две равные по времени части. Затем проводят проверку по F-критерию Фишера о равенстве дисперсий в сравниваемых группах: , где. Если расчетное значение меньше табличного при числе степеней свободыи, то гипотеза о равенстве дисперсий подтверждается и проверка равенства средних уровней осуществляется поt-критерию Стьюдента: , где.

Если при заданном уровне значимости и степени свободы , различия между средними уровнями ряда признаются несущественными, и ряд можно считать стационарным.

Прогнозирование на основе средних показателей динамики.

Скорость изменения уровней динамического ряда за определенный отрезок времени характеризуется средним абсолютным приростом. Предполагая его стабильным, прогноз можно дать в виде следующей экстраполяции: , где - прогнозируемый уровень,- уровень, принятый за базу для экстраполяции,- средний абсолютный прирост в единицу времени,- период упреждения.

Другим показателем динамики, который может быть использован в ориентировочном краткосрочном прогнозе, является средний коэффициент (темп) роста. Прогнозное значение уровня, исходя из среднего коэффициента роста, можно получить по формуле: , где - уровень, принятый за базу для экстраполяции,- средний коэффициент роста,- период упреждения.

Использование в экстраполяции средних показателей динамики относится в прогнозировании к классу наивных моделей. Вместе с тем в ряде случаев этот метод может найти применение как предварительный прогноз.

Аналитическое выравнивание и индексы сезонности.

Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции (тренда), характеризующей зависимость временного ряда от времени. Этот способ называют аналитическим выравниванием временного ряда.

В частности эта функция может быть представлена, например полиномом k – й степени:

.

Для полинома первой степени коэффициентыибудут находиться из системы уравнений: .

Для полинома второй степени коэффициенты,ибудут находиться из системы уравнений:

Сезонные колебания (сезонная неравномерность) – это сравнительно устойчивые внутригодичные колебания, т. е. когда из года в год в одни месяцы уровень явления повышается, а другие - снижается.

Измеряются сезонные колебания (сезонная волна) при помощи особых показателей, которые называются индексами сезонности. Индексы сезонности исчисляются по формуле: , где- средняя из фактических уровней одноименных месяцев;- общая средняя за исследуемый период.