
Boyarshinov_ChM_T3
.pdf
Fr k r F k Fz k z d Fr k r F k Fz k z d .
Векторная функция 1, согласно (4.5), имеет компоненты
|
|
|
|
|
|
|
|
|
|
1 |
|
|
, |
|
1 |
|
|
0, |
|
|
1 |
|
z |
0 |
, |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и предыдущее выражение приводится уравнению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
r m |
1 |
|
1 rz m |
|
|
1 |
m |
|
|
|
|
|
|
|
|
Fr 1d Fr 1d . |
|||||||||||||||||||||||||||
rr m |
|
1 |
r |
z |
|
|
|
1 |
|
d |
|
||||||||||||||||||||||||||||||||||||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Для векторных функций 2 |
и 3 уравнения имеют вид, соответственно, |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
z m |
|
|
|
|
|
|
|
|
|
|
F 1d F 1d , |
|||||||||||||||||||||
|
r m |
|
|
|
1 |
|
|
1 |
|
|
1 |
d |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
r r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
m |
1 |
|
zz m |
|
|
|
|
|
|
|
|
|
Fz 1d Fz 1d , |
|||||||||||||||||||||||||
|
zr m |
|
1 z |
|
|
|
|
|
1 |
|
|
1 |
d |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
и так далее для всех прочих функций k , |
|
|
|
k 4,5, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Учитывая, что для осесимметричного напряженно-деформированного |
||||||||||||||||||||||||||||||||||||||||||||||
состояния |
r |
0, z |
0, |
|
|
пробные |
|
|
функции |
|
|
k |
не |
|
|
зависят |
|
от угла , |
|||||||||||||||||||||||||||||
поверхностные нагрузки F |
0 |
|
и массовые силы F |
0 |
(в этом случае второе |
||||||||||||||||||||||||||||||||||||||||||
выражение обращается в тождество), приходим к системе уравнений |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
m |
|
k |
m |
|
|
|
|
rz m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
rr |
|
|
|
k |
|
|
|
|
k |
d Fr k d Fr kd , |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
m |
|
k zz |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1,m, |
||||||||||||||||||||
|
rz |
|
|
|
|
|
k |
d Fz k d Fz kd , |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
которая в матричной записи имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
rr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
i |
|
i |
|
0 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 x |
|
|
|
|
|
|
|
|
|
|
|
0 |
F |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
r |
|
|
|
|
|
|
i |
|
|||||||||||||||||||||||
|
|
|
r |
|
|
r |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|||||||||||
|
|
|
|
|
|
i |
i |
|
|
|
|
|
dV |
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
dV , |
||||||||||||||||||
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
x |
|
|
|
|
|
|
V |
0 |
|
|
|
|
|
|
|||||
|
0 |
|
|
0 |
|
|
|
|
|
|
zz |
|
|
|
|
|
|
z |
|
|
|
|
|
|
F |
|
|||||||||||||||||||||
|
|
|
|
|
z |
r |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
z |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Bk m d k F d k F d , |
k 1,m, |
|
(4.21) |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где
91

k |
k 0 |
|||
|
r |
r |
|
|
Bk |
k |
|||
|
0 |
0 |
||
z |
||||
|
|
|
||
k
z ,k
r
остальные обозначения введены ранее.
Для установления кинематических соотношений, как и ранее, вектор перемещений представляется в виде
|
|
m |
|
um |
ui |
i |
|
i 1 |
|
||
um |
|
m |
. |
vm |
|
|
|
|
|
vi |
i |
|
|
i 1 |
|
Для цилиндрической системы координат (с учетом осевой симметрии напряженно-деформированного состояния) связи компонент тензора деформации и вектора перемещений устанавливаются формулами
rr m |
|
m |
i , |
m |
|
|
|
m |
|
i , |
zz m |
|
m |
i , |
||||||
um ui |
um ui |
vm vi |
||||||||||||||||||
|
r |
i 1 |
r |
v |
|
u |
r |
|
i 1 |
|
r |
|
|
|
|
z |
i 1 |
z |
||
|
|
rz m |
m |
|
m |
|
|
i ui |
|
|
|
, |
|
|
||||||
|
|
|
|
|
m vi |
|
r |
|
i |
|
|
|
||||||||
|
|
|
|
r |
|
z |
i 1 |
|
|
|
|
z |
|
|
|
|
||||
iz
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
u |
|
m |
. |
|
i |
|
i |
|
T |
|
|
v |
|
Bi ui |
||
z |
i |
|
i 1 |
|
|
|
|
|
|
||
i |
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
Последовательная подстановка (4.15) и последнего выражения в соотношение (4.21) приводит к системе алгебраических уравнений метода взвешенных невязок для осесимметричной задачи механики деформируемого твердого тела, совпадающей по виду с выражением (4.18),
m |
|
|
|
|
Bk D Bi T d ui k F d k F d Bk R Td , |
k 1,m. |
|||
i 1 |
|
|
|
|
Подынтегральные выражения содержат интегралы по области , занимаемой конечным элементом. Для цилиндрических координат это соответствует
92

f r, ,z d f r, ,z rdrd dz 2 f r, ,z rdrdz.
|
|
p |
При определении коэффициентов матрицы жесткости конечного элемента приходится вычислять значения интегралов вида
|
rdrdz, |
|
drdz, |
|
i j drdz |
i |
i j |
r |
|||
|
|
|
|
||
p |
|
p |
|
p |
|
и другие. Даже при аппроксимации решения линейными пробными функциямиi r,z это представляет значительные трудности.
Практика использования метода взвешенных невязок показывает, что с приемлемой точностью такого вида интегралы можно заменять выражениями
f r,z rdrdz |
f r,z r drdz f r,z rSp , |
p |
p |
где r, z – координаты центра тяжести конечного элемента, Sp – как и ранее, площадь конечного элемента. Очевидно, что точность такого приближения повышается с уменьшением размеров конечных элементов.
Решение задач упругопластичности
Рассматривается частный случай связи напряжений и деформаций в теории малых упругопластических деформаций1 Г. Генки, определяющей пропорциональность девиаторов тензоров напряжений и деформаций:
eij sij , |
(4.22) |
|
eij ij |
ij 3, |
|
sij ij |
ij 3, |
|
где 11 22 33 . С помощью соотношения (4.22) устанавливается связь интенсивности деформации i (второго инварианта тензора деформации) с интенсивностью напряжения i (вторым инвариантом тензора напряжений),
|
2 |
|
2 |
|
3 |
|
2 |
i . |
i |
3eijeij |
|
3 |
|
2 sijsij |
|
3 |
1 А. А. Ильюшиным установлено, что закон малых упругопластических деформаций справедлив, по крайней мере, в тех случаях, когда процесс нагружения является простым. В частности, это имеет место, если внешние нагрузки изменяются пропорционально одному параметру. В этом случае для простого нагружения достаточно, чтобы i и i были связаны степенным соотношением вида i A i .
93

Принимая гипотезу единой кривой и учитывая условие пластического течения, i T i , параметр в соотношении (4.22) может быть определен в виде
|
3 i |
|
3 i |
(4.23) |
|
2 i |
|
2 T i . |
Метод переменных параметров упругости
С помощью соотношения (4.22) устанавливается связь компонент тензоров напряжений и деформаций,
|
|
s |
|
|
|
1 |
e |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
ij |
|
|
|
|
|
|
|
|
|
ij 3 |
|
|
|
. |
|||||||||||||
|
ij |
|
ij |
ij |
|
|
ij |
ij |
|
|
|
ij |
|
ij |
3 |
|
|
|
ij |
|
3 |
|
|||
С учетом зависимости между и , |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
3 2G |
E |
, |
|
|
|
|
|
|
(4.24) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
|
|
|
|
||
физические уравнения теории малых упругопластических деформаций принимают форму
ij |
|
1 |
ij |
ij |
E 1 2 |
|
31 2 . |
Полученное выражение может быть представлено в форме, аналогичной записи закона Гука для упругого деформирования (4.14)
|
|
E* |
|
|
|
E* * |
|
||||
ij |
1 * ij ij |
1 * 1 2 * . |
|||||||||
Из сопоставления двух последних выражений следует система уравнений |
|||||||||||
относительно параметров E*, * , |
|
|
|
|
|
||||||
|
E |
* |
|
|
1 , |
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
E* * |
|
|
|
E 1 2 |
|
|||
|
|
|
|
|
|
. |
|||||
1 |
* |
1 2 |
* |
|
3 1 2 |
||||||
|
|||||||||||
|
|
|
|
|
|||||||
Решение этой систему уравнений дает
* E 1 2 , 2E 1 2
E |
* |
|
3E |
|
2E 1 2 . |
94
Теперь соотношения теории малых упругопластических деформаций |
||||||||
записаны в форме, аналогичной соотношениям теории упругости, что позволяет |
||||||||
записать разрешающие соотношения метода взвешенных невязок в форме |
|
|||||||
m |
|
|
|
|
|
|
|
|
Bk D* Bi T d ui k F d k F d Bk R d , |
k 1,m, |
(4.25) |
||||||
i 1 |
|
|
|
|
|
|
|
|
эквивалентной выражению (4.18), полученному для случая упругого |
||||||||
деформирования материала. |
|
|
|
|
||||
i |
(1) |
|
|
|
|
|
||
|
|
i (2) |
|
|
|
|
|
|
|
|
|
i |
(3) |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
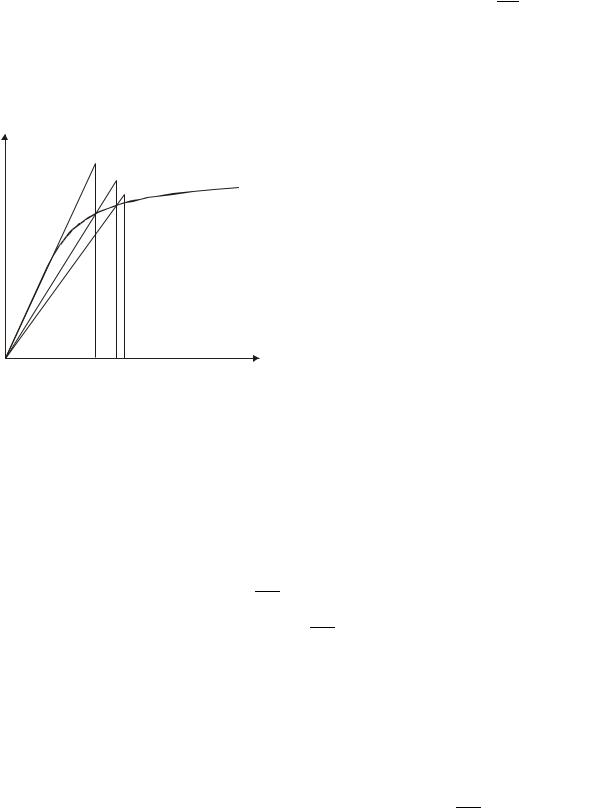
Рис. 4.6. Схема итераций метода |
||
|
|
|
|
|
|
переменных параметров упругости |
||
|
|
(1) |
(2) |
(3) |
|
|
|
|
|
i |
i |
i |
|
i |
|
|
|
Процесс решения строится в следующей последовательности.
1.Во всей рассматриваемой области напряженно-деформированное состояние предполагается упругим, то есть
1 2G 1
2G 1  E ,
E ,
вследствие чего * , E* E . Решением системы алгебраических уравнений (4.25) с граничными условиями, соответствующими поставленной задаче,
определяются перемещения ui , |
i 1,m. |
|
2. С использованием решения ui , |
i 1,m подсчитывается интенсивность |
|
деформаций i. Это, в свою очередь, позволяет с помощью диаграммыT i определить для каждого конечного элемента величину параметра
согласно выражению (4.23) и подсчитать значения переменных параметров упругости E*, * , то есть сформировать матрицу [D*] для каждого конечного элемента.
3. Формируется система уравнений (4.25) с вычисленными значениями
матрицы [D*], и вновь определяются векторы ui , |
i 1,m, |
m , |
m |
, подсчитываются параметры и вычисляются |
E*, * , |
и так далее. |
|
95

Итерационная процедура выполняется до тех пор, пока для двух соседних итераций s и s+1 выполняется условие
|
s 1 |
|
s |
|
s 1 |
s |
|
(4.26) |
|
|
max ij |
ij |
|||||
|
|
|
|
|
x , i, j 1,2,3 |
|
|
|
где > 0 – заданная погрешность вычислений. Геометрическая интерпретация итераций метода переменных параметров упругости показана на рис. 4.6.
Метод дополнительных нагрузок
Вновь, с использованием соотношения (4.22), связь девиаторов тензоров напряжений и деформаций представляется в виде
s |
|
|
1 |
e |
2Ge |
|
1 |
|
|
|
|
|
|
2G e . |
|||||
|
ij |
|
ij |
ij |
|
|
ij |
||
Это выражение, с учетом зависимости (4.24), позволяет записать соотношение между компонентами тензоров напряжений и деформаций,
ij sij ij 2Geij ij
3
|
ij |
ij |
|
ij |
|
|
2G |
1 |
|
2G |
3 |
|
3 |
|
|
||||
|
|
|
|
|
|
|
|||
2G |
|
ij |
|
2G |
1 |
ij |
|
2G |
|
||
|
3 |
|
|
1
2G eij
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ij |
|
ij |
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ij |
|
ij |
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2G |
|
|
|
|
1 |
|
|
|
|
|
|
|
ij |
ij |
2G |
|
|
ij |
ij |
3 |
. |
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Вводя, в соответствии с законом Гука (4.14), упругие напряжения
ije ij 2G ij
и дополнительные напряжения
|
* |
|
2G |
1 |
|
|
|
|
|
, |
||
ij |
|
|
|
ij |
ij |
3 |
|
|||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
полные напряжения можно представить в виде
ij eij *ij .
Подстановка этого соотношения в уравнения (4.0) и (4.3) приводит к соотношениям
~ |
|
~e |
|
~* |
|
|
|
|
~e |
|
~* |
F 0, |
x , |
|||||
F |
|
F |
|
|||||||||||||||
|
~ |
|
~e |
~* |
|
|
|
~e |
|
|
~* |
|
|
|
|
. |
|
|
n |
|
n |
|
|
n |
|
n |
|
F, |
x |
|
|||||||
|
|
|
|
|
|
|
|
|
F |
|
||||||||
96

Вводя обозначения
~* |
* |
, |
|
~* |
F |
* |
, |
F |
|
n |
|
|
два полученных уравнения можно представить в виде
~e |
F F |
* |
0, x , |
|
|
|
|||
|
~e |
|
* |
, x F . |
n |
F F |
|||
Теперь задачу упругопластичности можно рассматривать как задачу упругости с дополнительными массовыми силами F* и поверхностными нагрузками F*. Разрешающие соотношения (4.18) метода взвешенных невязок теперь представляются в форме
m
Bk D Bi T d ui k F d k F d Bk R d
i 1 |
|
|
|
|
F |
|
|
k |
F* d k F* d , |
k 1,m |
|
(4.27) |
||
F |
|
|
|
|
|
|
Итерационное решение задачи упругопластичности строится следующим |
||||||
образом. |
|
|
|
|
|
|
1. Во всей рассматриваемой области принимается |
1 |
2G 1 E , в |
||||
результате чего |
*ij 0, |
F* 0, |
F* 0. |
Это |
означает, что |
|
первоначально во всей области предполагается чисто упругое деформирование. Решением системы алгебраических уравнений (4.27)
без слагаемых |
k F* d , |
k F* d определяются перемещения |
||
ui , |
|
F |
|
|
i 1,m. Затем, |
согласно формулам (4.17) и (4.15), определяются |
|||
деформации { m} |
и |
напряжения { m} во всех конечных элементах, |
||
аппроксимирующих исследуемую область .
2.По известным компонентам тензора деформаций подсчитывается интенсивность деформаций i. Это, в свою очередь, позволяет по
диаграмме |
T i |
определить величину параметра согласно |
|
выражению |
(4.23), |
вычислить |
дополнительные напряжения *ij и |
массовые силы F* |
для каждого |
конечного элемента, дополнительные |
|
поверхностные нагрузки F* на границе ГF области.
3. Формируется система уравнений (4.27) с дополнительными слагаемыми
k F* d , |
k F* d . Вновь определяется решение |
задачи – |
||||
F |
|
|
|
|
|
|
векторы ui , |
i 1,m, |
m , |
m , |
подсчитываются параметры и |
||
вычисляются |
|
*ij , F*, |
F*, |
и так |
далее. Итерационная |
процедура |
97

выполняется до тех пор, пока, как и в предыдущем методе переменных параметров упругости, для двух соседних итераций выполняется условие (4.26).
Геометрическая интерпретация приведена на рис. 4.7.
Рис. 4.7. Схема метода дополнительных нагрузок
метода |
дополнительных |
нагрузок |
i |
e |
|
|
* |
|
|
|
|
|
i |
i |
Контрольные вопросы и задания
Обоснуйте принцип построения системы пробных функций для пространственных (трехмерных) задач.
Покажите, что система пробных функций (4.5) для пространственных задач является полной и замкнутой.
Воспроизведите построение разрешающих соотношений метода Галеркина для уравнений равновесия деформируемого твердого тела с использованием конечно-элементной аппроксимации.
Сформулируйте основные гипотезы плоско-деформированного напряженного-деформированного состояния.
Сформулируйте основные гипотезы плоско-напряженного напряженного-деформированного состояния.
Сформулируйте основные гипотезы осесимметричного напряженногодеформированного состояния.
Обоснуйте процедуру ансамблирования конечных элементов. Каким образом учитываются кинематические и силовые граничные условия при получении системы линейных алгебраических уравнений метода Галеркина?
Укажите различия в системах разрешающих соотношений метода Галеркина при моделировании плоско-напряженного и плоскодеформированного состояний твердого тела.
98
Укажите различия в системах разрешающих соотношений метода Галеркина при моделировании осесимметричного и плоскодеформированного состояний твердого тела.
Сформулируйте гипотезу единой кривой, используемую в теории малых упругопластических деформаций.
Сформулируйте условие пластического нагружения деформируемого материала.
Сформулируйте условия простого нагружения материала при упругопластическом деформировании.
Обоснуйте идею решение упругопластических задач с помощью последовательности решений задач упругости.
Опишите идею метода переменных параметров упругости. Приведите схему этого метода.
Опишите идею метода дополнительных нагрузок. Приведите схему этого метода.
99
5 . З А Д А Ч И М Е Х А Н И К И Ж И Д К О С Т И
Пусть |
v vxi vy j vzk – |
вектор скорости частицы жидкости. Вводятся |
|||
векторные |
(в общем случае) |
|
j zk и |
||
функции тока xi y |
|||||
|
|
j zk , определяемые соотношениями |
|
||
завихренности xi y |
|
||||
|
|
|
|
|
|
|
|
u |
, |
(5.0) |
|
|
|
|
|
|
|
|
|
u. |
|
||
Учитывая, что
i
xx
i
u  x
x
vx
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
y |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|||||||||
y |
z |
z |
|
x |
z |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
j |
|
|
|
|
|
x k , |
||||||||||
|
|
|
|
y |
|
|
z |
|
|
|
|
z |
|
|
x |
|
|
x |
|
y |
|
|
|||||
y |
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
vz |
|
v |
|
|
|
vx |
|
vz |
|
|
|
v |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
y |
z |
|
|
|
y |
|
|
|
|
|
|
y |
|
vx |
|
|
|||||||||||
|
y |
z |
i |
|
|
z |
x |
j |
|
|
x |
|
k , |
|
|||||||||||||
vy |
vz |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в компонентной форме соотношения (5.0) имеют вид
vx z y , |
vy |
x z , |
vz |
y x , |
|||||||||||||||
|
|
y |
|
z |
|
|
|
|
z |
|
x |
|
|
x |
|
y |
|||
|
|
|
v |
z |
vy |
, |
|
|
|
v |
x |
v |
z , |
|
|
vy |
|
v |
x . |
x |
|
z |
y |
|
|
z |
|
|
|||||||||||
|
|
y |
|
|
|
z |
x |
|
x |
|
y |
||||||||
В дальнейшем рассматривается плоское (двухмерное) течение жидкости. В этом случае приведенные выражения упрощаются. Функция тока (здесь и далее индекс z опускается) связана с компонентами vx и vy вектора скорости выражениями
vx |
, |
vy |
. |
(5.1) |
|
y |
|
x |
|
Функция завихренности (вихрь скорости) определяется также одной компонентой,
vy |
|
v |
x , |
(5.2) |
|
|
|||
x |
|
y |
|
|
100
